Cho đường tròn (O) đường kính BC và 1 điểm A nằm trên đường tròn (A ≠ B và C). Qua O, kẻ tia Ox // AC, tia Ox cắt AB tại D.
a. Chứng minh: OD ⊥ AB và từ đó suy ra D là trung điểm của AB.
b. Tiếp tuyến tại B của (O) cắt tia Ox tại E. Chứng minh: EA cũng là tiếp tuyến của (O).
c. Tia CA cắt tia BE tại F. Chứng minh: Tia CE đi qua trung điểm I của đường cao AH.
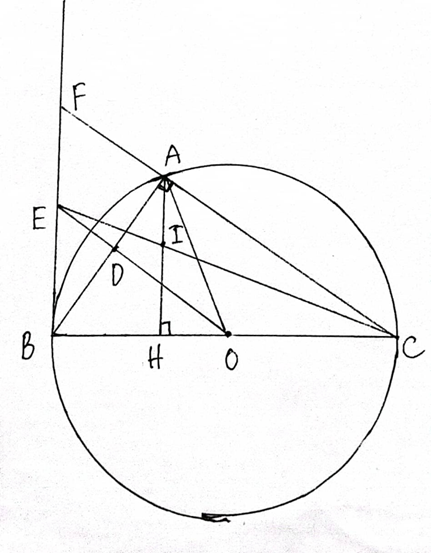
a. A ∈ (O) đường kính BC \( \Rightarrow \widehat {BAC} = 90^\circ \)(góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow AB \bot AC\)
Mà Ox // AC \( \Rightarrow Ox \bot AB\) hay OD \( \bot AB\)
Ta có: OA = OB
⇒ ∆OAB cân tại O có đường cao OD
⇒ OD là đường trung tuyến
⇒ D là trung điểm AB
b. Xét ∆OAB cân tại O, \(OD \bot AB \Rightarrow OD\) là phân giác \(\widehat {AOB}\)
Xét ∆OAE và ∆OBE có: OE chung; \(\widehat {AOE} = \widehat {BOE}\)(OE phân giác \(\widehat {AOB}\)); OA = OB
\( \Rightarrow \Delta OAE = \Delta OBE\left( {c.g.c} \right) \Rightarrow \widehat {OAE} = \widehat {OBE} = 90^\circ \)(BE là tiếp tuyến tại A của (O).
c. Xét ∆BCF có: O là trung điểm BC; OE // FC (vì Ox // AC)
⇒ OE là đường trung bình ∆BCF ⇒ E là trung điểm BF ⇒ BE = EF
Ta có: AH ⊥ BC; BF ⊥ BC ⇒ AH // BF
⇒ \(\frac{{AI}}{{EF}} = \frac{{CI}}{{CE}} = \frac{{IH}}{{BE}}\)(Định lí Talet)
Mà EF = BE ⇒ AI = IH ⇒ I là trung điểm AH (Gọi I = CE ∩ AH).