Lời giải
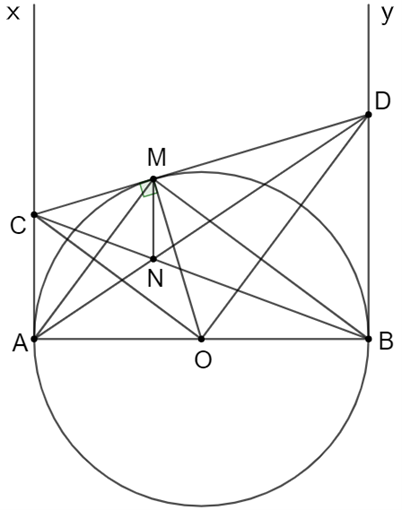
a) Ax là tiếp tuyến của đường tròn (O)
Þ Ax ^ AB Þ AC ^ AB (1)
By là tiếp ruyến của đường tròn (O)
Þ By ^ AB Þ BD ^ AB (2)
Từ (1) và (2) Þ AC // BD
Áp dụng định lý Ta-lét với AC // BD ta có:
\[\frac{{AC}}{{BD}} = \frac{{CN}}{{NB}} \Rightarrow \frac{{CN}}{{AC}} = \frac{{NB}}{{BD}}\] (đpcm)
b) Theo tính chất 2 tiếp tuyến cắt nhau, ta có:
• Ax và CD là 2 tiếp tuyến cắt nhau tại C Þ CA = CM;
• By và CD là 2 tiếp tuyến cắt nhau tại D Þ DB = DM.
Ta có: \(\frac{{CN}}{{AC}} = \frac{{NB}}{{BD}} \Rightarrow \frac{{CN}}{{CM}} = \frac{{NB}}{{MD}} \Rightarrow \frac{{CN}}{{NB}} = \frac{{CM}}{{MD}} \Rightarrow \frac{{CN}}{{CB}} = \frac{{CM}}{{CD}}\).
Vậy MN // BD (Theo định lí Ta-lét).
Mà BD ^ AB Þ MN ^ AB.
c) Ta có: CA = CM (cmt) và OA = OM = R
Þ OC là đường trung trực của đoạn thẳng MA
Þ OC cũng là đường phân giác của ∆OMA
\[ \Rightarrow \widehat {MOC} = \widehat {AOC} = \frac{1}{2}\widehat {MOA}\] (3)
Lại có: DB = DM (cmt) và OB = OM = R
Þ OD là đường trung trực của đoạn thẳng MB
Þ OD cũng là đường phân giác của ∆OMB
\[ \Rightarrow \widehat {MOD} = \widehat {BOD} = \frac{1}{2}\widehat {MOB}\] (4)
Từ (3) và (4) ta suy ra
\[\widehat {MOC} + \widehat {MOD} = \frac{1}{2}\widehat {MOA} + \frac{1}{2}\widehat {MOB}\]
\( = \frac{1}{2}\left( {\widehat {MOA} + \widehat {MOB}} \right) = \frac{1}{2}\widehat {AOB} = \frac{1}{2} \cdot 180^\circ = 90^\circ \)
\( \Rightarrow \widehat {COD} = 90^\circ \) (đpcm).

