Cho đường tròn (O; 4 cm), đường kính AB. Lấy điểm H thuộc đoạn OA sao cho OH = 1 cm. Kẻ dây cung CD vuông góc với AB tại H.
a) Chứng minh: \(\Delta ABC\) vuông và tính độ dài AC.
b) Tiếp tuyến tại A của (O) cắt BC tại E. Chứng minh \(\Delta BCD\) cân và \(\frac{{EC}}{{DH}} = \frac{{EA}}{{DB}}\).
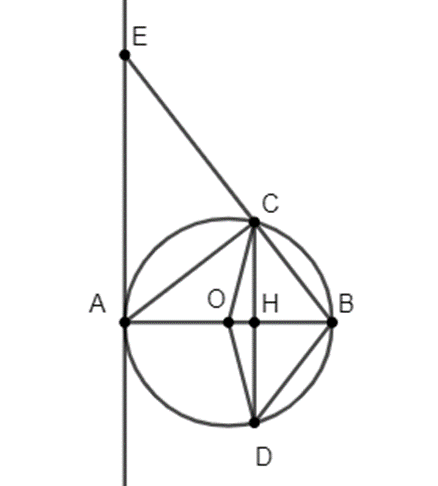
a) \(\Delta ABC\) nội tiếp đường tròn đường kính AB
\( \Rightarrow \Delta ABC\) vuông tại C (đpcm)
\( \Rightarrow \)AC2 = AH.AB = (R – OH).
2R = (4 – 1).2.4 = 24
Suy ra \(AC = 2\sqrt 6 \) (cm)
b) \(\Delta OHC = \Delta OHD\)(cạnh huyền – cạnh góc vuông)
Suy ra HC = HD (hai cạnh tương ứng)
\( \Rightarrow \)BH là trung tuyến của \(\Delta BCD\) mà BH cũng là đường cao.
\( \Rightarrow \)\(\Delta BCD\)cân tại B (đpcm)
Ta có: AC\( \bot \)CB \( \Rightarrow \Delta CAE\) vuông tại E
Mà \(\widehat {CBH} = \widehat {EAC}\) (cùng phụ với \(\widehat {CAB}\))
\( \Rightarrow \Delta CAE\)∽\(\Delta HBC\) (g.g)
\( \Rightarrow \frac{{AE}}{{BC}} = \frac{{EC}}{{HC}}\)
MÀ \(\Delta BCD\)cân tại B, BH là trung tuyến.
\( \Rightarrow \)BC = BD và HC = DH
\( \Rightarrow \frac{{AE}}{{BD}} = \frac{{EC}}{{DH}}\) (đpcm)