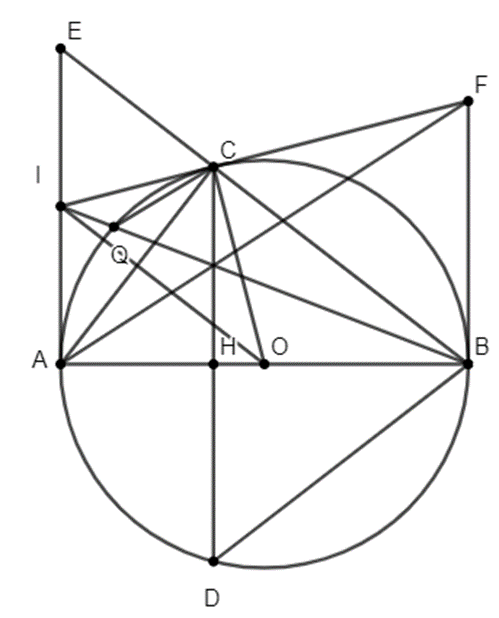
a) OA = OB = 4, OH = 1 \( \Rightarrow \) AH = 3, HB = 5
Ta có: AB là đường kính của (O) \( \Rightarrow \)\(\widehat {ACB} = 90^\circ \)
\( \Rightarrow \)∆ABC vuông tại C.
Mà CH\( \bot \)AB \( \Rightarrow \)CH2 = HA. HB = 15
\( \Rightarrow \)AC2 = CH2 + HA2 = 24 \( \Rightarrow \)\(AC = 2\sqrt 6 \).
b) Vì AB\( \bot \)CD \( \Rightarrow \)AB là trung trực của CD
\( \Rightarrow \)BC = BD \( \Rightarrow \)∆CBD cân tại B.
Lại có: \(\widehat {EAC} = \widehat {CBA} = \widehat {HBD}\)
\( \Rightarrow \)∆ECA ᔕ ∆DHB (g.g)
\( \Rightarrow \frac{{EC}}{{DH}} = \frac{{EA}}{{DB}}\).
c) Vì I, O là trung điểm AE, AB
\( \Rightarrow \)IO // EB \( \Rightarrow \)IO\( \bot \)AC (BE\( \bot \)AC) \( \Rightarrow \)A, C đối xứng với nhau qua OI
\( \Rightarrow \)\(\widehat {ICO} = \widehat {IAO} = 90^\circ \)
\( \Rightarrow \)IC là tiếp tuyến của (O).
\( \Rightarrow \)\(\widehat {ICQ} = \widehat {CBI}\)
d) Gọi AF ∩ BI = {G}
Vì IC, IA là tiếp tuyến của (O) \( \Rightarrow \)IC = IA tương tự FC = FB
Mà AI // BF \( \Rightarrow \)\(\frac{{IG}}{{GB}} = \frac{{IA}}{{BF}} = \frac{{CI}}{{CF}}\)
\( \Rightarrow \)GC // BF \( \Rightarrow \)GC\( \bot \)AB \( \Rightarrow \)C, G, H thẳng hàng
\( \Rightarrow \)IB, HC, AF đồng quy.