Cho đường tròn (O; 2 cm) và điểm M nằm ngoài (O) sao cho hai tiếp tuyến MA, MB kẻ từ M đến (O) vuông với nhau tại M.

a) Tứ giác MBOA là hình gì? Vì sao?

b) Gọi C là điểm bất kì trên cung nhỏ AB. Qua C kẻ tiếp tuyến với đường tròn cắt MA, MB theo thứ tự ở D và E. Tính chu vi tam giác MDE.

Lời giải

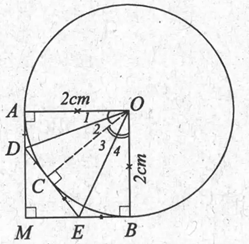
a) Vì MA, MB là tiếp tuyến của (O)

Nên MA ⊥ OA, MB ⊥ OB

Suy ra \(\widehat {OAM} = \widehat {OBM} = 90^\circ \)

Vì MA ⊥ MB nên \(\widehat {BMA} = 90^\circ \)

Xét tứ giác OBMA có \(\widehat {OAM} = \widehat {OBM} = \widehat {BMA} = 90^\circ \)

Nên OBMA là hình chữ nhật

Mà OA = OB

Suy ra OBMA là hình vuông                                  

Vậy OBMA là hình vuông.

b)Vì OBMA là hình vuông

Nên MA = MB = OA = OB = 2 cm

Xét (O) có DA, DC là hai tiếp tuyến cắt nhau tại D

Suy ra DA = DC

Xét (O) có EB, EC là hai tiếp tuyến cắt nhau tại E

Suy ra EB = EC

Chu vi tam giác MED bằng

ME + ED + MD = ME + EC + CD + MD = ME + EB + DA + MD

= MB + MA = 2 + 2 = 4 (cm)

Vậy chu vi tam giác MDE bằng 4 cm.