Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI. a) Chứng minh vecto BN - vecto BA = vecto MB. b) Tìm các đ
28
18/05/2024
Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.
a) Chứng minh \[\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \].
b) Tìm các điểm D, C sao cho \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {ND} ;\,\,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
Trả lời
Lời giải
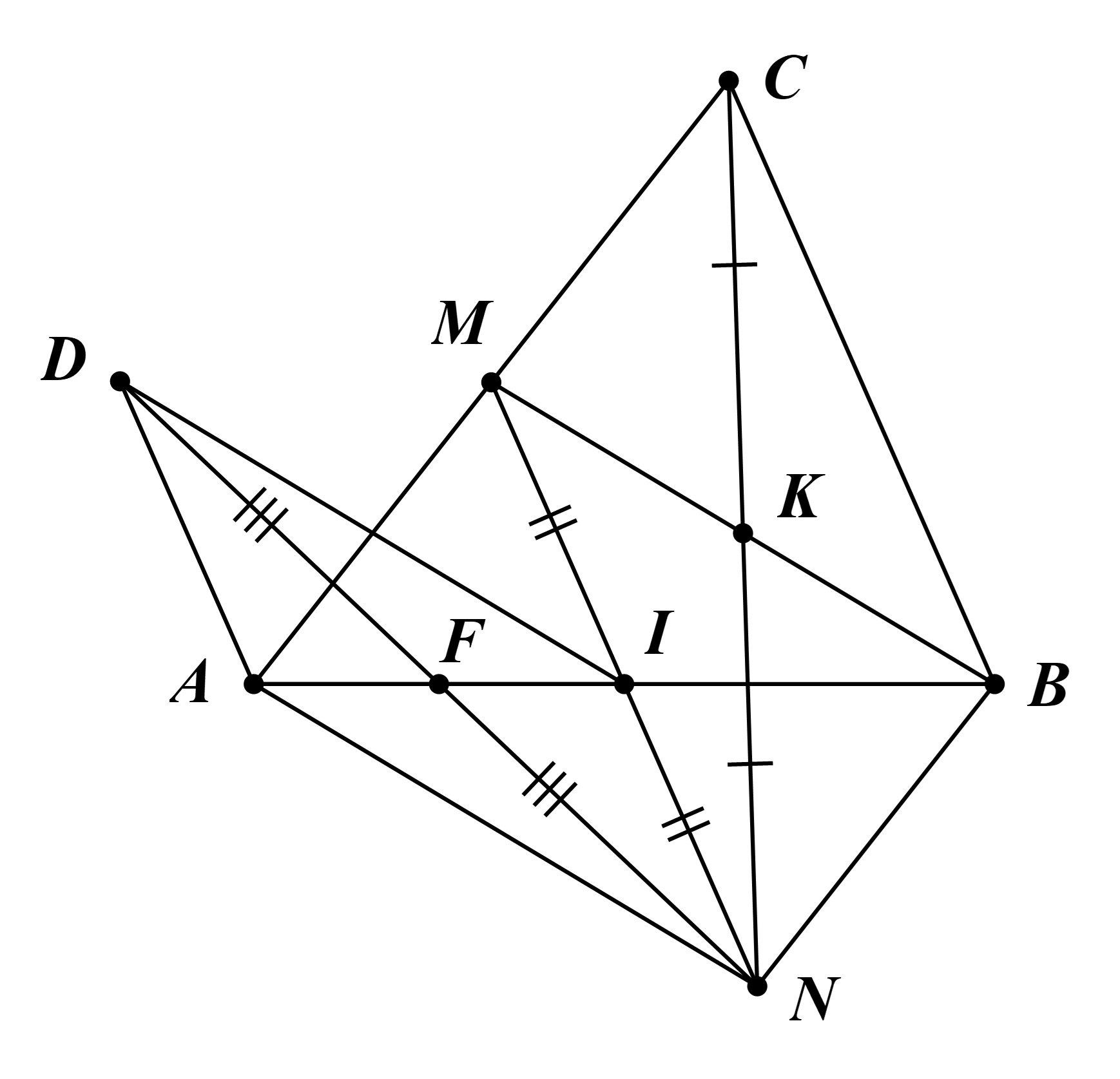
a) Ta có I là trung điểm AB (giả thiết) và I là trung điểm MN (do IN = MI).
Do đó tứ giác AMBN là hình bình hành.
Suy ra \(\overrightarrow {AN} = \overrightarrow {MB} \) và \(\overrightarrow {BN} = \overrightarrow {MA} \).
Ta có \(VT = \overrightarrow {AN} = \overrightarrow {MB} = VP\).
Vậy ta có điều phải chứng minh.
b) Gọi F là trung điểm AI.
Suy ra \(\overrightarrow {NA} + \overrightarrow {NI} = 2\overrightarrow {NF} \).
Theo đề, ta có \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {ND} \).
\( \Leftrightarrow 2\overrightarrow {NF} = \overrightarrow {ND} \).
Suy ra F là trung điểm của ND.
Mà F là trung điểm AI.
Vậy D là điểm thỏa mãn tứ giác ADIN là hình bình hành.
Ta có \(\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NM} + \overrightarrow {NB} = 2\overrightarrow {NK} \), với K là trung điểm MB.
Theo đề, ta có \(\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).
\( \Leftrightarrow 2\overrightarrow {NK} = \overrightarrow {NC} \).
Suy ra K là trung điểm NC.
Mà K là trung điểm MB.
Vậy C là điểm thỏa mãn tứ giác BCMN là hình bình hành.

