Cho đoạn thẳng AB có trung điểm I. M là điểm tùy ý không nằm trên đường thẳng AB. Trên MI kéo dài, lấy một điểm N sao cho IN = MI.

a) Chứng minh \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \).

b) Tìm các điểm D, C sao cho\(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).

Lời giải

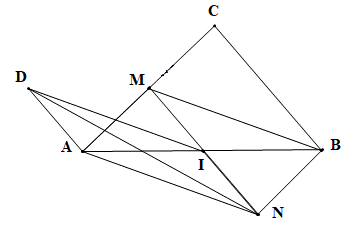
a) Ta có: I là trung điểm của MN

Suy ra \(\overrightarrow {BM} + \overrightarrow {BN} = 2\overrightarrow {BI} \)

Mà \(\overrightarrow {BI} = \overrightarrow {IA} = \frac{1}{2}\overrightarrow {AB} \)

Suy ra \(\overrightarrow {BM} + \overrightarrow {BN} = \overrightarrow {BA} \)

Suy ra \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \)

Vậy \(\overrightarrow {BN} - \overrightarrow {BA} = \overrightarrow {MB} \).

b) Kẻ ID // AN sao cho ID = AN

Suy ra ANID là hình bình hành

Do đó \(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} \) (quy tắc hình bình hành)

Ta có \(\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NM} + \overrightarrow {NB} \)

Kẻ MC // BN và MC = BN

Suy ra MCBN là hình bình hành

Do đó \(\overrightarrow {NM} + \overrightarrow {NB} = \overrightarrow {NC} \) (quy tắc hình bình hành)

Vậy ANID là hình bình hành, MCBN là hình bình hành thì\(\overrightarrow {NA} + \overrightarrow {NI} = \overrightarrow {N{\rm{D}}} ,\overrightarrow {NM} - \overrightarrow {BN} = \overrightarrow {NC} \).