Cho bốn điểm A, B, C, D nằm trên đường tròn tâm O sao cho AB = CD. Chứng minh góc AOB = góc COD

Bài 27 trang 75 SBT Toán 7 Tập 2: Cho bốn điểm A, B, C, D nằm trên đường tròn tâm O sao cho AB = CD. Chứng minh $\widehat{AOB}=\widehat{COD}$.

Trả lời

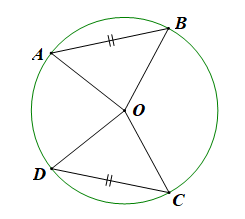
Vì bốn điểm A, B, C, D nằm trên đường tròn tâm O nên OA = OB = OC = OD.

Xét $∆$OAB và $∆$OCD có:

AO = OC (chứng minh trên),

AB = DC (giả thiết),

OB = OD (chứng minh trên),

Suy ra $∆$OAB = $∆$OCD (c.c.c).

Do đó $\widehat{AOB}=\widehat{COD}$ (hai góc tương ứng).

Vậy $\widehat{AOB}=\widehat{COD}$.

Xem thêm lời giải bài tập Toán lớp 7 Kết nối tri thức hay, chi tiết khác:

Bài 1. Tổng các góc của một tam giác

Bài 2. Quan hệ giữa góc và cạnh đối diện. Bất đẳng thức tam giác

Bài 3. Hai tam giác bằng nhau

Bài 4. Trường hợp bằng nhau thứ nhất của tam giác: cạnh – cạnh – cạnh

Bài 5. Trường hợp bằng nhau thứ hai của tam giác: cạnh – góc – cạnh

Bài 6. Trường hợp bằng nhau thứ ba của tam giác:

Bài 7. Tam giác cân