Cho biết (bz - cy) / a = (cx - az) / b = (ay - bx) / c. Chứng minh x : y : z = a : b : c
Cho biết \(\frac{{b{\rm{z}} - cy}}{a} = \frac{{c{\rm{x}} - az}}{b} = \frac{{ay - b{\rm{x}}}}{c}\). Chứng minh x : y : z = a : b : c.
Ta có \(\frac{{b{\rm{z}} - cy}}{a} = \frac{{c{\rm{x}} - az}}{b} = \frac{{ay - b{\rm{x}}}}{c} = \frac{{a(b{\rm{z}} - cy)}}{{{a^2}}} = \frac{{b(c{\rm{x}} - az)}}{{{b^2}}} = \frac{{c(ay - b{\rm{x)}}}}{{{c^2}}}\)
\( = \frac{{ab{\rm{z}} - acy}}{{{a^2}}} = \frac{{bc{\rm{x}} - baz}}{{{b^2}}} = \frac{{cay - cb{\rm{x}}}}{{{c^2}}}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
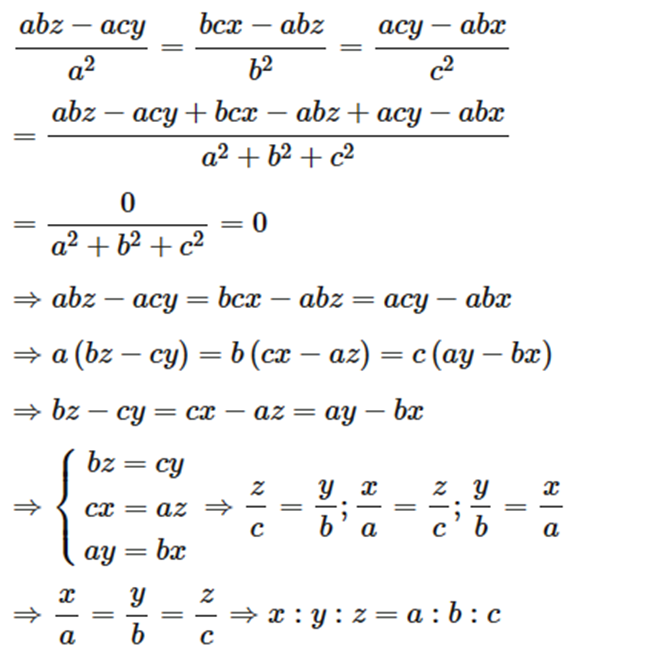
Vậy x : y : z = a : b : c.