Cho ∆ADC vuông tại a có đường cao AH, \(\widehat D = 65^\circ \), AH = 3 cm. Trên nửa mặt phẳng bờ DC chứa điểm A vẽ tia Cx song song với AD, trên Cx lấy điểm B sao cho CB = DA. Tính khoảng cách từ B đến AD, độ dài đoạn BD và diện tích tam giác ABD.
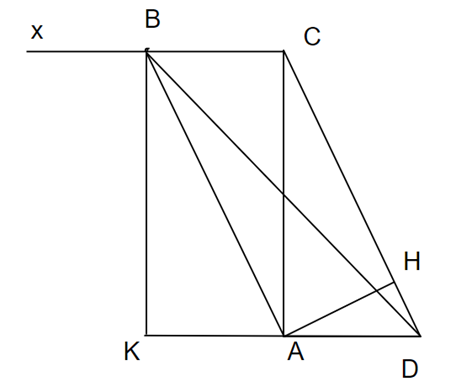
Kẻ BK ⊥ AD
Xét ∆ADC\((\widehat A = 90^\circ ):\widehat {ADC} = 65^\circ \Rightarrow \widehat {ACD} = 25^\circ \)
Khi đó: \(CA = \frac{{AH}}{{\sin \widehat C}} = \frac{3}{{\sin 25^\circ }}\)
Dễ thấy BCAK là hình chữ nhật \( \Rightarrow BK = AC = \frac{3}{{\sin 25^\circ }}(cm)\)và BC = AK
⟹ DA = AK (= BC) ⇒ DK = 2DA
Ta có: \(DA = \frac{{AH}}{{\sin \widehat {CDA}}} = \frac{3}{{\sin 25^\circ }}(cm)\)
\(DK = 2DA = \frac{6}{{\sin 25^\circ }}(cm)\)
Áp dụng định lí Pytago vào ∆BKD vuông tại K có \(B{K^2} + K{D^2} = B{D^2}\)
\( \Leftrightarrow {\left( {\frac{3}{{\sin 25^\circ }}} \right)^2} + {\left( {\frac{6}{{\sin 25^\circ }}} \right)^2} = B{D^2} \Leftrightarrow B{D^2} = \frac{{45}}{{{{\sin }^2}25^\circ }} \Leftrightarrow BD = \frac{{3\sqrt 5 }}{{\sin 25^\circ }}(cm)\)
Ta có \({S_{ABD}} = {S_{BKD}} - {S_{BAK}} = \frac{{BK.KD}}{2} - \frac{{AK.BK}}{2} = \frac{{BK}}{2}(KD - AK)\)
\( = \frac{{BK.AD}}{2} = \frac{{\frac{3}{{\sin 25^\circ }}.\frac{3}{{\sin 25^\circ }}}}{2} = \frac{{18}}{{\sin 25^\circ }}(c{m^2})\).