Cho ∆ABC vuông tại A, đường cao AH. Gọi HD, HE lần lượt là đường cao của ∆AHB và ∆AHC. Chứng minh rằng:

a) \(\frac{{A{B^2}}}{{A{C^2}}} = \frac{{HB}}{{HC}}\).

b) \(\frac{{A{B^3}}}{{A{C^3}}} = \frac{{BD}}{{EC}}\).

Lời giải:

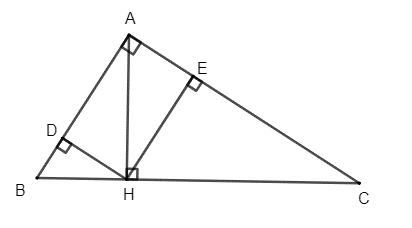
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được: \(\left\{ {\begin{array}{*{20}{c}}{A{B^2} = BH.BC}\\{A{C^2} = CH.BC}\end{array}} \right.\)

\( \Rightarrow \frac{{A{B^2}}}{{A{C^2}}} = \frac{{BH.BC}}{{CH.BC}} = \frac{{HB}}{{HC}}\). (đpcm)

b) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:

\(BD.BA = B{H^2} \Leftrightarrow BD = \frac{{H{B^2}}}{{AB}}\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:

\(CE.CA = C{H^2} \Leftrightarrow EC = \frac{{H{C^2}}}{{AC}}\)

Ta có: \(\frac{{BD}}{{EC}} = \frac{{H{B^2}}}{{A{B^2}}}:\frac{{H{C^2}}}{{AC}}\)

\( \Leftrightarrow \frac{{BD}}{{EC}} = \frac{{H{B^2}}}{{AB}}.\frac{{AC}}{{H{C^2}}}\)

\( \Leftrightarrow \frac{{BD}}{{EC}} = {\left( {\frac{{HB}}{{HC}}} \right)^2}.\frac{{AC}}{{AB}}\)

\( \Leftrightarrow \frac{{BD}}{{EC}} = {\left( {\frac{{A{B^2}}}{{A{C^2}}}} \right)^2}.\frac{{AC}}{{AB}}\)

\( \Leftrightarrow \frac{{BD}}{{EC}} = {\left( {\frac{{AB}}{{AC}}} \right)^4}.\frac{{AC}}{{AB}}\)

\( \Leftrightarrow \frac{{BD}}{{EC}} = \frac{{A{B^4}}}{{A{C^4}}}.\frac{{AC}}{{AB}}\)

\( \Leftrightarrow \frac{{BD}}{{EC}} = \frac{{A{B^3}}}{{A{C^3}}}\). (đpcm)