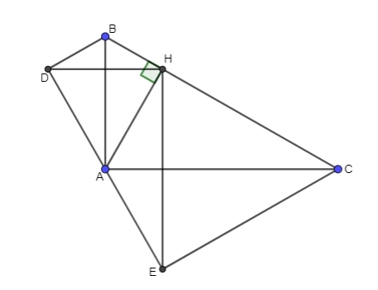
Cho ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là các điểm đối xứng của H qua các cạnh AB, AC.

Trả lời

a) Do D đối xứng với H qua đoạn AB nên $\Delta ADH$cân tại A 

$\Delta ADH$có AB là đường cao đồng thời là phân giác 

$\Rightarrow \widehat{\text{DAB}}\text{ = }\widehat{\text{HAB}}$

Tương tự với $\Delta AHE\Rightarrow \widehat{\text{HAC}}\text{ = }\widehat{\text{EAC}}$

Ta có : 

$\widehat{\text{DAE}}\text{ = }\left(\widehat{\text{DAH}}\right)\text{ + }\left(\widehat{\text{HAE}}\right)\text{ = 2.}\left(\widehat{\text{BAH}}\right)\text{ + 2.}\left(\widehat{\text{HAC}}\right)\text{ = 2.}\left(\widehat{\text{BAH}}\text{ + }\widehat{\text{HAC}}\right)\text{ = 2.90 = 180⇒}$ D, A, E thẳng hàng 

Nhận thấy 

$\Delta AHC$ đối xứng với $\Delta AEC$ qua đoạn thẳng AC $\Rightarrow \widehat{\text{AHC}}\text{ = }\widehat{\text{AEC}}{\text{ = 90}}^0$(1)

Tương tự , ta cũng có : $\widehat{\text{BHA}}\text{ = }\widehat{\text{BDA}}{\text{ = 90}}^{\text{0 }}$(2)

Từ (1) và (2) $\Rightarrow$ BD // EC (do 2 góc trong cùng phía bù nhau)

b) Ta có : $\Delta BHA$ đồng dạng với $\Delta AHC$ 

Suy ra tỷ lệ $\frac{\text{BH}}{\text{AH}}\text{ = }\frac{\text{AH}}{\text{HC}}\iff {\text{AH}}^{\text{2}}\text{ = BH . HC}$

Mà BH = BD , HC = CE

$\Rightarrow {\text{AH}}^{\text{2}}\text{ = BD . CE}$

$\iff {\text{4AH}}^{\text{2}}\text{ = 4BD . CE}$

$\iff {\left(\text{2AH}\right)}^{\text{2}}\text{ = 4BD . CE}$ (Do AD = AH = AE)

$\iff {\text{DE}}^{\text{2}}\text{ = 4BD . CE}$.

c) Ta có: AD = AH (tính chất đối xứng), AH = AE (tính chất đối xứng)

Suy ra AD = AE mà A, D, E thẳng hàng nên A là trung điểm của DE.

Xét tam giác vuông ABC, vuông tại A, có:

$\frac{1}{A{H}^2}=\frac{1}{A{B}^2}+\frac{1}{A{C}^2}=\frac{1}{3^2}+\frac{1}{4^2}=\frac{25}{144}\Rightarrow AH=\frac{12}{5}$

$\Rightarrow AD=AE=AH=\frac{12}{5}$

⇒ DE = $\frac{24}{5}$ cm.

Xét tam giác ABC vuông tại A có:

$$\begin{gathered} \tan \widehat{ABC}=\frac{AC}{AB}=\frac{4}{3}\Rightarrow \sin \widehat{ABC}=\frac{4}{5} \\ \Rightarrow \sin \widehat{ADH}=\frac{4}{5} \end{gathered}$$

Xét tam giác DHE vuông tại H, có:

$\sin \widehat{ADH}=\frac{EH}{ED}=\frac{EH}{\frac{24}{5}}=\frac{4}{5}\Rightarrow EH=\frac{96}{25}\Rightarrow DH=\frac{72}{25}$

Vậy diện tích tam giác DEH là: $\frac{1}{2}DH.EH=\frac{1}{2}.\frac{96}{25}.\frac{72}{25}\approx 5,5$ (đvdt).