Lời giải:
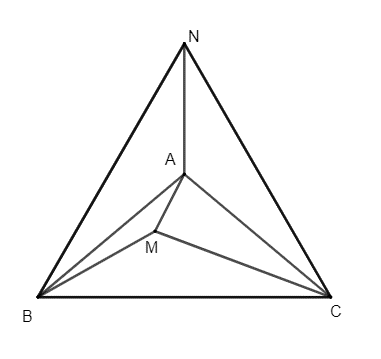
Trên nửa mặt phẳng bờ BC có chứa A vẽ \(\Delta BCN\) đều
Xét ∆ABN và ∆CAN có:
AB = AC (Do ∆ABC cân tại A)
BN = CN (do \(\Delta BCN\) đều)
AN chung
Do đó, ∆ABN = ∆ACN (c.c.c)
\( \Rightarrow \widehat {BNA} = \widehat {CNA} = \frac{{\widehat {BNC}}}{2} = \frac{{60^\circ }}{2} = 30^\circ \).
Tam giác ABC cân tại A có \(\widehat A = 100^\circ \) nên \(\widehat {BCA} = \widehat {ABC} = \frac{{180^\circ - 100^\circ }}{2} = 40^\circ \).
Mặt khác, \(\widehat {BCA} + \widehat {ACN} = \widehat {BCN}\)\( \Rightarrow 40^\circ + \widehat {ACN} = 60^\circ \Rightarrow \widehat {ACN} = 20^\circ \).
\(\widehat {MCA} + \widehat {MCB} = \widehat {ACB}\)\( \Rightarrow \widehat {MCA} + 20^\circ = 40^\circ \) \( \Rightarrow \widehat {MCA} = 20^\circ \)
Xét ∆CBM và ∆CAN có:
BC = CN (do \(\Delta BCN\) đều)
\(\widehat {MBC} = \widehat {CNA} = 30^\circ ,\widehat {MCB} = \widehat {ACN} = 20^\circ \)
Do đó, ∆CBM = ∆CNA (g.c.g)
⇒ CM = CA
⇒ ∆CMA cân tại C
⇒ \(\widehat {MAC} = \widehat {AMC}\)
⇒ \(\widehat {MAC} = \left( {180^\circ - \widehat {MCA}} \right):2 = 80^\circ \)
Ta có: \(\widehat {MBC} + \widehat {ABM} = \widehat {ABC}\).
\( \Rightarrow \widehat {ABM} = 40^\circ - 30^\circ = 10^\circ \)
Ta có: \(\widehat {MAB} + \widehat {MAC} = \widehat {BAC} \Rightarrow \widehat {BAM} = 100^\circ - 80^\circ = 20^\circ \)
Xét ∆AMB có: \(\widehat {AMB} + \widehat {MAB} + \widehat {ABM} = 180^\circ \)
\( \Rightarrow \widehat {AMB} = 180^\circ - 10^\circ - 20^\circ = 150^\circ \)
Vậy \(\widehat {AMB} = 150^\circ \).