Cho a và b là hai số dương khác nhau thỏa mãn a - b = căn bậc hai (1 - b^2
Cho a và b là hai số dương khác nhau thỏa mãn \(a - b = \sqrt {1 - {b^2}} - \sqrt {1 - {a^2}} \).
Chứng minh a2 + b2 = 1.
Ta có
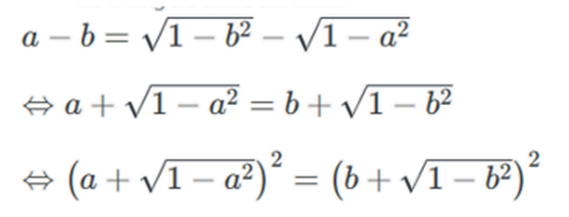
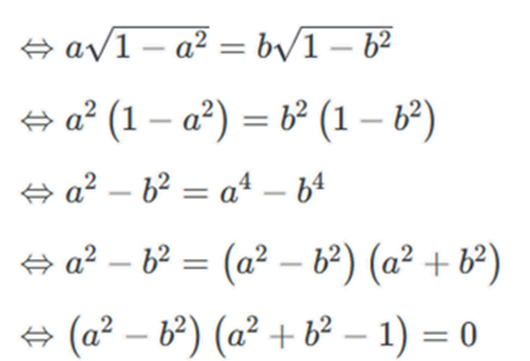
\( \Leftrightarrow \left[ \begin{array}{l}{a^2} - {b^2} = 0\\{a^2} + {b^2} - 1 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}a = b\\{a^2} + {b^2} = 1\end{array} \right.\)
Mà a ≠ b
Suy ra a2 + b2 = 1.