Cho a, b, c đôi một khác nhau thỏa mãn (a + b + c)^2 = a^2 + b^2 + c^2

Đề bài: Cho a, b, c đôi một khác nhau thỏa mãn (a + b + c)² = a² + b² + c².

Tính $P=\frac{a^2}{a^2+2bc}+\frac{b^2}{b^2+2ac}+\frac{c^2}{c^2+2ab}$ .

Trả lời

Hướng dẫn giải:

Ta có (a + b + c)² = a² + b² + c²

⇔ a² + b² + c² + 2ab + 2bc + 2ac = a² + b² + c²

⇔ 2ab + 2bc + 2ac = 0

⇔ ab + bc + ac = 0

⇔ $\left\{\begin{array}{l}\text{ab = - bc - ac}\\ \text{bc = - ab - ac}\\ \text{ac = - ab - bc}\end{array}\right.$

Thay $\left\{\begin{array}{l}\text{ab = - bc - ac}\\ \text{bc = - ab - ac}\\ \text{ac = - ab - bc}\end{array}\right.$  vào biểu thức P ta có

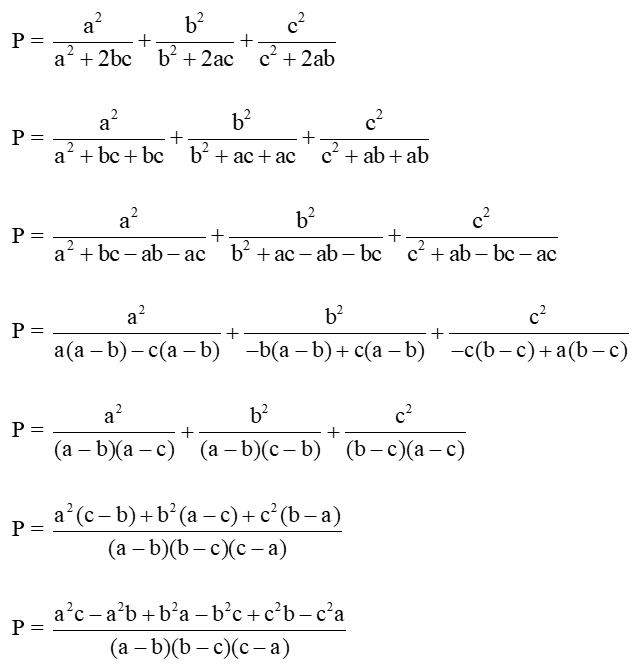
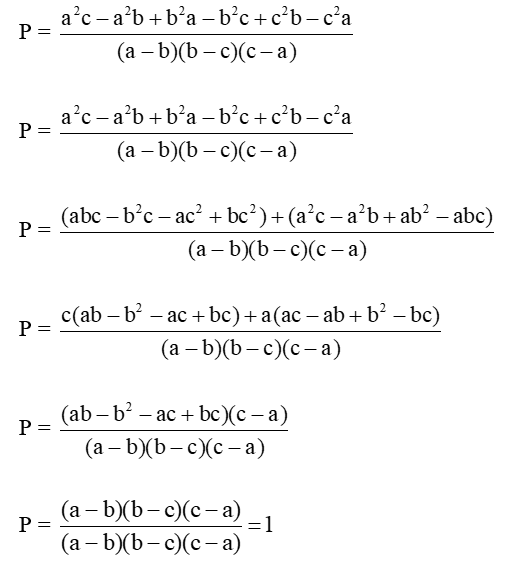
Vậy P = 1.