Cho 3 số thực dương x, y, z thỏa mãn x + y + z + 2 = xyz. Chứng minh rằng x + y + z + 6

Đề bài: Cho 3 số thực dương x, y, z thỏa mãn x + y + z + 2 = xyz. Chứng minh rằng

$x+y+z+6\ge 2\left(\sqrt{yz}+\sqrt{zx}+\sqrt{xy}\right)$

Trả lời

Lời giải:

Theo đề, ta có x + y + z + 2 = xyz

⇔ (xy + yz + zx) + 2(x + y + z) + 3 = xyz + xy + yz + zx + x + y + z + 1

⇔ (x + 1)(y + 1) + (y + 1)(z + 1) + (z + 1)(x + 1) = (xy + x + y + 1)(z + 1)

⇔ (x + 1)(y + 1) + (y + 1)(z + 1) + (z + 1)(x + 1) = (x + 1)(y + 1)(z + 1)

$\iff \frac{1}{z+1}+\frac{1}{x+1}+\frac{1}{y+1}=1$.

Đặt $a=\frac{1}{x+1};b=\frac{1}{y+1};c=\frac{1}{z+1}$

Khi đó ta có a + b + c = 1 và

$x=\frac{1-a}{a}=\frac{b+c}{a};y=\frac{1-b}{b}=\frac{a+c}{b};z=\frac{1-c}{c}=\frac{a+b}{c}$ .

Ta có

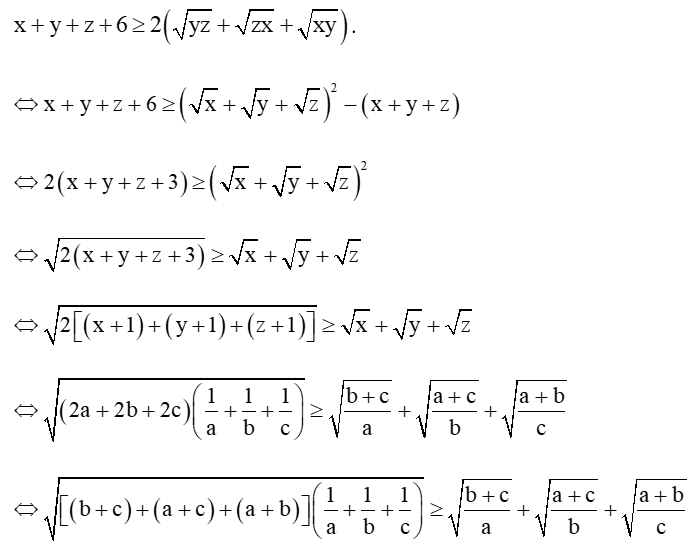
Dấu “=” xảy ra $\iff a=b=c=\frac{1}{3}\iff x=y=z=2$ .

Vậy ta có điều phải chứng minh.