Cho các số a, b, c khác nhau đôi một và thoả mãn a^2 – 2b = b^2 – 2c = c^2 – 2a

Đề bài: Cho các số a, b, c khác nhau đôi một và thoả mãn a² – 2b = b² – 2c = c² – 2a.

Trả lời

Hướng dẫn giải:

Ta có: a² – 2b = c² – 2a

⇔ a² –  c² = 2b – 2a

⇔ (a – c)(a + c) = 2(b – a)

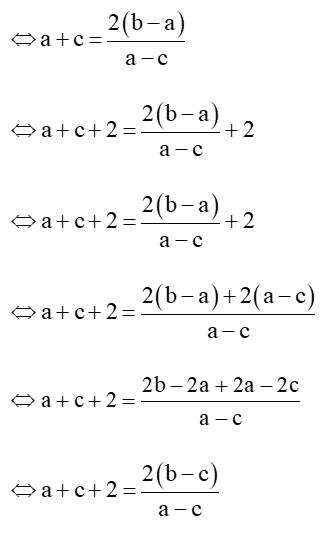
Chứng minh tương tự ta có:

$a+b+2=\frac{2\left(a-c\right)}{a-b}$ và $b+c+2=\frac{2\left(b-a\right)}{b-c}$

Suy ra A = (a + b + 2)(b + c + 2)(c + a + 2)

               $=\frac{2\left(a-c\right)}{a-b}.\frac{2\left(b-a\right)}{b-c}.\frac{2\left(b-c\right)}{a-c}=-8$

Vậy A = – 8.