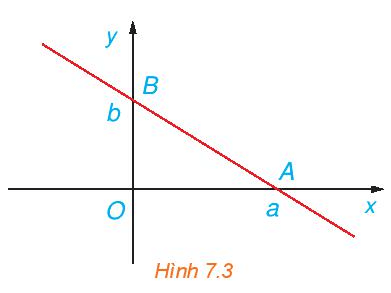
(Phương trình đoạn chắn của đường thẳng). Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H.7.3)
1k
11/04/2023
Bài 7.5 trang 34 Toán 10 Tập 2: (Phương trình đoạn chắn của đường thẳng)
Chứng minh rằng, đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 (H.7.3) có phương trình là xa+yb=1.
Trả lời
Ta có: →AB=(0−a;b−0)=(−a; b).
Suy ra đường thẳng AB có một vectơ chỉ phương là →AB=(−a;b) nên nó có một vectơ pháp tuyến là →n=(b; a).
Do đó phương trình tổng quát của đường thẳng AB đi qua điểm A và nhận →n làm vectơ pháp tuyến là: b(x – a) + a(y – 0) = 0 hay bx + ay – ab = 0 (1).
Do ab ≠ 0 nên ta chia cả hai vế của (1) cho ab, ta được:
bxab+ayab−abab=0ab
⇔xa+yb−1=0
⇔xa+yb=1
Vậy đường thẳng đi qua hai điểm A(a; 0), B(0; b) với ab ≠ 0 có phương trình là xa+yb=1.

