Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha

Đề bài: Bác Năm dự định trồng khoai lang và khoai mì trên mảnh đất có diện tích 8 ha. Nếu trồng 1 ha khoai lang thì cần 10 ngày công và thu được 20 triệu đồng. Nếu trồng 1 ha khoai mì thì cần 15 ngày công và thu được 25 triệu đồng. Bác Năm cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Năm chỉ có thể sử dụng được không quá 90 ngày công cho việc trồng khoai lang và khoai mì.

Trả lời

Hướng dẫn giải:

Gọi x, y (ha) lần lượt là diện tích trồng khoai lang và khoai mì (x, y ≥ 0).

Theo bài ra ta có hệ bất phương trình: $\left\{\begin{array}{l}10x+15y\le 90\\ x+y\le 8\\ x\ge 0\\ y\ge 0\end{array}\right.$ .

Số tiền thu được khi trồng x ha khoai lang và y ha khoai mì là F(x; y) = 20x + 25y (triệu đồng).

Bài toán trở thành: Tìm x, y thỏa mãn hệ bất phương trình $\left\{\begin{array}{l}10x+15y\le 90\\ x+y\le 8\\ x\ge 0\\ y\ge 0\end{array}\right.$  để F(x; y) = 20x + 25y lớn nhất.

Biểu diễn miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}10x+15y\le 90\\ x+y\le 8\\ x\ge 0\\ y\ge 0\end{array}\right.$  lên mặt phẳng tọa độ.

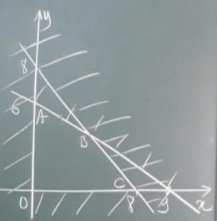
Miền nghiệm của hệ bất phương trình $\left\{\begin{array}{l}10x+15y\le 90\\ x+y\le 8\\ x\ge 0\\ y\ge 0\end{array}\right.$ là miền tứ giác OABC với O là gốc tọa độ, A(0; 6), B(6; 2), C(8; 0).

Ta có: F(0; 0) = 0

F(0; 6) = 20 . 0 + 25 . 6 = 150

F(6; 2) = 20 . 6 + 25 . 2 = 170

F(8; 0) = 20. 8 + 25 . 0 = 160

Do đó, F(x; y) lớn nhất tại (x; y) = (6; 2).

Vậy bác Năm cần trồng 6 ha khoai lang và 2 ha khoai mì để thu được nhiều tiền nhất.