Cách tìm tiệm cận ngang
I. Phương pháp giải
Để tìm tiệm cận ngang của một đồ thị hàm số, ta có các bước sau:
Bước 1: Ta tìm tập xác định của hàm số.
Bước 2: Tính giới hạn của hàm số đó tại vô cực (nếu có). Từ đó ta xác định được đường tiệm cận ngang.

Giải: Tập xác định hàm số là: D = R
Ta có: lim x→-∞ y = 0, lim x→+∞ y = 0
Vậy đồ thị hàm số có đúng một đường tiệm cận ngang là y = 0.
Các công thức tính tiệm cận ngang:
Tiệm cận ngang của đồ thị hàm số ac:

Công thức tính Tiệm cận ngang của hàm phân thức hữu tỉ:

Công thức tính Tiệm cận ngang của hàm phân thức vô tỉ:

Cách tính tiệm cận ngang bằng máy tính casio
Hướng dẫn:
Tìm đường tiệm cận ngang bằng máy tính, ta sẽ tính giá trị gần đúng của lim x→+∞y và lim x→-∞y.
Tính lim x→+∞y: Ta tính giá trị của hàm số tại một giá trị x rất lớn. Ta lấy x = 10^9 . Kết quả là giá trị gần đúng của lim x→+∞y.
Tính lim x→-∞y: Ta tính giá trị của hàm số tại một giá trị x rất nhỏ. Ta lấy x = - 10^9. Kết quả là giá trị gần đúng của lim x→-∞y.
=> Tính giá trị hàm số tại một giá trị x, ta dùng chức năng CALC trên máy tính.
Ví dụ:
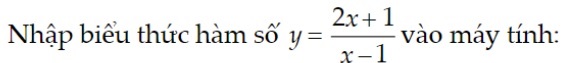

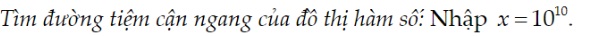

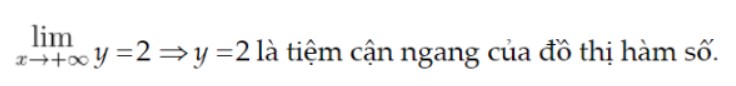
Các bài tập tiệm cận ngang:



II. Bài tập vận dụng
Câu 1: Tìm tiệm cận ngang của đồ thị hàm số:
Hướng dẫn giải
Vậy là tiệm cận ngang của đồ thị hàm số.
Câu 2: Cho hàm số có đồ thị (C). Tìm khẳng định đúng trong các khẳng định sau:
A. (C) có đúng một tiệm cận ngang y = 1
B. (C) có đúng một tiệm cận ngang y = -1
C. (C) không có tiệm cận ngang
D. (C) có hai tiệm cận ngang là y = 1 và y = -1
Hướng dẫn giải
Vậy y =1 và y = -1 là hai tiệm cận ngang của đồ thị hàm số (C)
Đáp án D
Câu 3: Cho đồ thị hàm số . Tìm tất cả giá trị tham số m để đồ thị hàm số có tiệm cận ngang.
| A. |
B. |
| C. |
D. |
Hướng dẫn giải
Ta có:
Đồ thị hàm số có tiệm cận ngang khi và chỉ khi bậc của tử bé hơn bậc của mẫu và tồn tại
Đáp án A
Xem thêm các dạng bài tập hay, có đáp án:
30 Bài tập Tìm tham số m để hàm số có tiệm cận (2024) cực hay, có đáp án
60 Bài tập về Đường tiệm cận (có đáp án năm 2024)
30 Bài tập về tiệm cận của hàm số (2024) cực hay, có đáp án chi tiết
30 Bài tập Tìm điều kiện của tham số m để phương trình lượng giác có nghiệm (2024) có đáp án
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án




