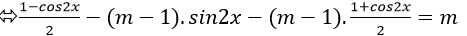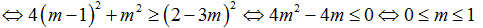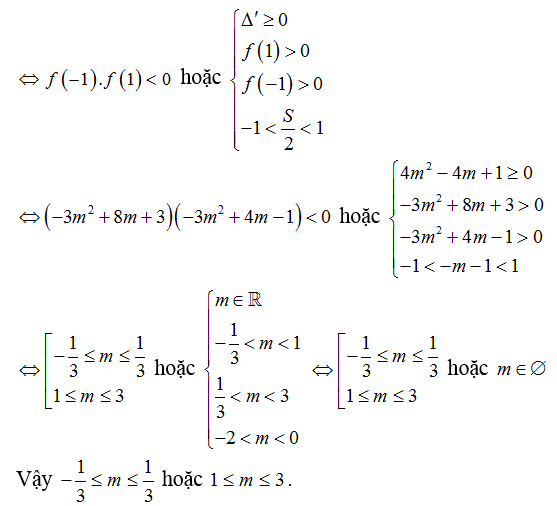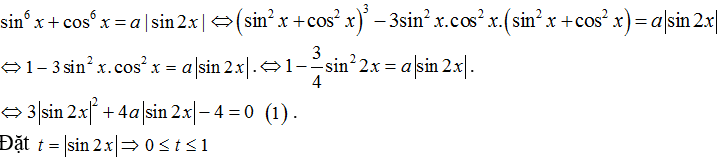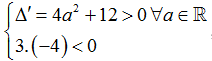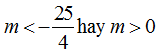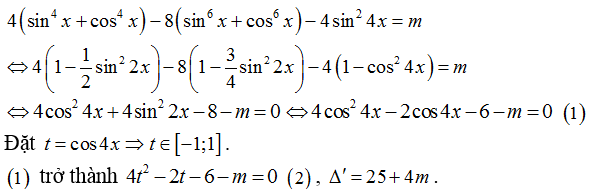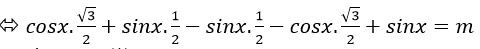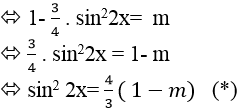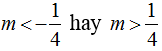30 Bài tập Tìm điều kiện của tham số m để phương trình lượng giác có nghiệm (2024) có đáp án

Tìm điều kiện của tham số m để phương trình lượng giác có nghiệm

1. Phương pháp giải

+ Phương trình a. sinx+ b=0 hoặc a.cosx+ b=0 ( với a ≠ 0) có nghiệm nếu:

- 1 ≤ sinx( hoặc cosx) ≤ 1.

+ Xét phương trình a.sin² x + bsinx+ c= 0 hoặc a.cos² x+ b. cosx+ c= 0 ( với a ≠ 0) :

Đặt sinx= t ( hoặc cosx = t) phương trình đã cho trở thành:

at² + bt + c= 0 (*)

để phương trình đã cho có nghiệm nếu phương trình (*) có nghiệm t₀ và -1 ≤ t₀ ≤ 1

2. Ví dụ minh họa

Ví dụ 1. Tìm tất cả giá trị của m để phương trình sin2x -2(m-1)sinxcosx-(m-1)cos2x=m có nghiệm?

A.0≤m≤1

B.m > 1

C.0 < m < 1

D.m≤0

Lời giải

Ta có: sin2 x- 2(m -1) sinx. cosx – ( m – 1) cos2 x= m

Ta có: 

⇒ 1- cos2x -2 (m- 1) .sin2x- ( m- 1) . ( 1 + cos2x) = 2m

⇒ 1- cos2x -2(m-1)sin2x – m+ 1 – (m-1).cos2x – 2m= 0

⇒ -2(m -1) sin2x – mcos2x= 3m - 2

Phương trình có nghiệm

Ta có: 

Chọn A.

Ví dụ 2. Để phương trình: sin² x+2(m+1).sinx – 3m(m-2)= 0 có nghiệm, các giá trị thích hợp của tham số m là:

A. .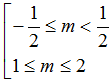

B. .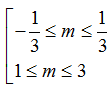

C. .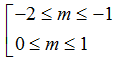

D. .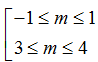

Lời giải

Đặt t = sinx.

Điều kiện .

Phương trình trở thành: t² + 2(m+1).t – 3m(m- 2)= 0 (1).

Đặt f(t) = t² + 2(m+1)t – 3m(m- 2).

Phương trình đã cho có nghiệm thuộc đoạn [-1;1] khi phương trình (1) có một nghiệm thuộc [-1;1] hoặc có hai nghiệm thuộc [-1;1]

Chọn B.

Ví dụ 3: Để phương trình 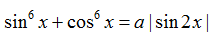 có nghiệm, điều kiện thích hợp cho tham số là:

A. .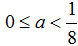

B. .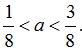

C. .

D. .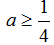

Lời giải

Phương trình (1) trở thành 3t²+ 4at – 4= 0 (2).

Để phương trình (1) có nghiệm thì phương trình (2) phải có nghiệm trong đoạn .

Xét phương trình (2), ta có:

nên (2) luôn có hai nghiệm phân biệt trái dấu.

Chọn D.

Ví dụ 4. Cho phương trình 2sinx+ cos90⁰ = m. Tìm điều kiện của m để phương trình đã cho có nghiệm?

A. - 2 ≤ m ≤ 2

B. - 1 ≤ m ≤ 1

C. - 4 ≤ m ≤ 4

D. Đáp án khác

Lời giải

Ta có: 2sinx+ cos90⁰= m

⇒ 2sinx + 0= m

⇒ sinx= m/2 (*)

Với mọi x ta luôn có: - 1 ≤ sinx ≤ 1

⇒ để phương trình đã cho có nghiệm khi và chỉ khi:

- 1 ≤ m/2 ≤ 1 ⇒ - 2 ≤ m ≤ 2

Chọn A.

Ví dụ 5. Cho phương trình: 4(sin⁴ x + cos⁴ x ) -8(sin⁶ x + cos⁶ x) -4sin² 4x = m trong đó m là tham số. Để phương trình là vô nghiệm, thì các giá trị thích hợp của m là:

A. .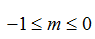

B.

C.

D.

Lời giải

Ta có:

+ Ta tìm điều kiện của m để phương trình có nghiệm. Rồi từ đó suy ra các giá trị của m để phương trình đã cho vô nghiệm.

(1) có nghiệm thì (2) phải có nghiệm thoả t₀ thuộc [-1;1] .

Chọn D.

Ví dụ 6. Cho phương trình cos(x-30⁰) + sin( x+ 60⁰)= m. Tìm điều kiện của m để phương trình đã cho có nghiệm?

A.0 ≤ m ≤ 1

B. -1 ≤ m ≤ 2

C. - 1 ≤ m ≤ 1

D. Đáp án khác

Lời giải

Ta có: cos(x- 30⁰) - sin(x+ 60⁰) + sinx = m

⇒ cosx . cos30⁰+ sinx. sin30⁰ - sinx. cos60⁰ - cosx. sin60⁰ + sinx= m

⇒ sinx= m (*)

Với mọi x ta luôn có: - 1 ≤ sinx ≤ 1 nên để phương trình đã cho có nghiệm khi và chỉ khi phương trình (*) có nghiệm

⇒ - 1 ≤ m ≤ 1

Chọn C.

Ví dụ 7. Có bao nhiêu giá trị nguyên của m để phương trình: 

 có nghiệm

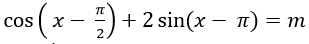
A. 2

B.4

C. 3

D.1

Lơì giải

Ta có: 

⇒ sinx - 2sinx = m

⇒ - sinx = m ⇒ sinx= - m

Với mọi x ta luôn có: - 1 ≤ sinx ≤ 1

⇒ để phương trình đã cho có nghiệm khi và chỉ khi:

- 1 ≤ -m ≤ 1 ⇒ - 1 ≤ m ≤ 1

⇒ m∈{ -1;0;1}

Chọn C.

Ví dụ 8: Cho phương trình cos⁶ x + sin⁶ x= m. Tìm điều kiện của m để phương trình đã cho có nghiệm?

A. 1/4 ≤ m ≤ 1

B. 1/2 ≤ m ≤ 1

C. 1/2 ≤ m ≤ 2

D. Đáp án khác

Lời giải

Ta có: cos⁶ x + sin⁶ x= m

⇒ (cos² x+ sin² x) . (cos⁴ x – cos²x. sin² x+ sin⁴ x) =m

⇒ 1.[ (cos²x+ sin² x)² – 3.cos² x. sin² x= m

Với mõi ta a luôn có: - 1 ≤ sin2x ≤ 1 nên 0 ≤ sin² 2x ≤ 1

Do đó; để phương trình đã cho co nghiệm khi và chỉ khi phương trình (*) có nghiệm

Chọn B.

3. Bài tập vận dụng (có đáp án)

Câu 1:Cho phương trình cos( x+ y) – cos( x-y) = m. Tìm điều kiện của m để phương trình đã cho có nghiệm.

A. -3 ≤ m ≤ 1

B. -2 ≤ m ≤ 2

C. – 3 ≤ m ≤ 1

D. - 4 ≤ m ≤ 2

Câu 2:Cho phương trình sin⁶ x- cos⁶ x + cos2x= m. Biết rằng khi m thuộc đoạn [a; b] phương trình đã cho có nghiệm. Tính a+ b

A. – 2

B. -1

C. 0

D. 1

Câu 3:Để phương trình 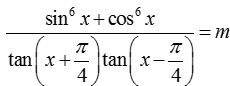 có nghiệm, tham số m phải thỏa mãn điều kiện:

A. -1 ≤ m < -1/4

B. -2 ≤ m ≤ -1

C.0 ≤ m ≤ 2

D.(- 1)/4 ≤ m ≤ 0

Câu 4: Để phương trình: 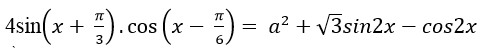 có nghiệm, tham số a phải thỏa điều kiện:

A.- 1 ≤ a ≤ 0 .

B. - 2 ≤ a ≤ 2.

C. - 1/2 ≤ m ≤ 1/4.

D. - 2 ≤ m ≤ 0

Câu 5:Cho phương trình: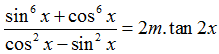 , trong đó m là tham số. Để phương trình có nghiệm, các giá trị thích hợp của m là

A.

B.

C.

D.

Câu 6:Cho phương trình cos( 90⁰- x)+ sin( 180⁰- x) + sinx= 3m. Có bao nhiêu giá trị nguyên của tham số m để phương trình đã cho có nghiệm

A. 3

B. 4

C. 2

D .5

Câu 7:Cho phương trình: sin² x+ (m-1) sinx – m = 0. Tìm điều kiện của tham số m để phương trình trên có nghiệm.

A.m > 2

B. m < 1

C. 1 < m < 10

D.Phương trình luôn có nghiệm với mọi m

Câu 8:Cho phương trình: cosx. sinx – 2m– 2sinx+ m.cosx= 0.Tìm điều kiện của m để phương trình đã cho có nghiệm.

A.0 ≤ m ≤ 1

B. -1 ≤ m ≤ 2

C. - 2 ≤ m ≤ 1

D. -1 ≤ m ≤ 1

Câu 9:Cho phương trình cos2x+ 4cosx+ m= 0. Tìm điều kiện của m để phương trình đã cho có nghiệm?

A. -7 ≤ m ≤ 1

B. -5 ≤ m ≤ 2

C. – 6 ≤ m ≤ 2

D. - 4 ≤ m ≤ 2

Câu 10:Cho phương trình sin2x+ 2sin² x+ 4cos² x=m. Tìm điều kiện của tham số m để phương trình đã cho có nghiệm?

A. -3√2 ≤ m ≤ 3√2

B. 3- √2 ≤ m ≤ √2+3

C. 2- √2 ≤ m ≤ √2+2

D. -2√2 ≤ m ≤ 2√2

Xem thêm các dạng bài tập toán hay khác:

20 Bài tập về cách tìm tập xác định của hàm số lượng giác (2024) có đáp án

150 Bài tập về hàm số lượng giác (có đáp án năm 2024) - Toán 11

100 Bài tập về phương trình lượng giác cơ bản (có đáp án năm 2024)

70 Bài tập về một số phương trình lượng giác thường gặp (có đáp án năm 2024)

500 Bài tập Toán 11 chương 1: Hàm số lượng giác và phương trình lượng giác (có đáp án năm 2024)