60 Bài tập về Phép trừ phân số (có đáp án năm 2024) - Toán lớp 4

Bài tập về Phép trừ phân số

Kiến thức cần nhớ

Lý thuyết: 

Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.

Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi trừ hai phân số đó.

Ví dụ: Tính: $\frac{7}{8}-\frac{3}{8}$

Lời giải:

Ta có: $\frac{7}{8}-\frac{3}{8}= \frac{7-3}{8}=\frac{5}{8}$

Các dạng bài tập toán phép trừ phân số

Dạng 1: Trừ hai phân số có cùng mẫu số

Phương pháp:

Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.

Ví dụ: Phép trừ $\frac{15}{29}-\frac{8}{29}$ có kết quả bằng bao nhiêu?

Lời giải:

Ta có: 

$\frac{15}{29}-\frac{8}{29}= \frac{15-8}{29}=\frac{7}{29}$

Vậy phép trừ $\frac{15}{29}-\frac{8}{29}$ có kết quả bằng $\frac{7}{29}$ .

Dạng 2: Phép trừ hai phân số khác mẫu số

Phương pháp:

Muốn trừ hai phân số khác mẫu số, ta quy đồng mẫu số hai phân số rồi trừ hai phân số đó.

Trường hợp trừ hai phân số khác mẫu số mà mẫu số của phân số thứ nhất chia hết cho mẫu số của phân số thứ hai thì ta quy đồng phân số thứ hai sau đó thực hiện phép trừ hai phân số đó.

Ví dụ 1: Kết quả của phép trừ $\frac{4}{5}-\frac{1}{7}$ bằng bao nhiêu?

Lời giải:

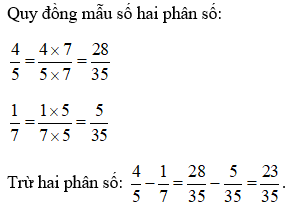
Ví dụ 2: Tính:  $\frac{4}{3}-\frac{2}{6}$.

Lời giải:

Ta có: $\frac{4}{3}-\frac{2}{6}=\frac{4}{3}-\frac{1}{3}=\frac{4-1}{3}=\frac{3}{3}=1$

Ví dụ 3: Kết quả của phép trừ $5-\frac{13}{4}$ là một phân số có tử số lớn hơn mẫu số bao nhiêu đơn vị?

Lời giải:

Ta có: $5-\frac{13}{4}=\frac{20}{4}-\frac{13}{4}=\frac{7}{4}$.

Kết quả của phép trừ  là phân số có tử số bằng 7, mẫu số bằng 4.Tử số lớn hơn mẫu số 7 – 4 = 3 ( đơn vị).

Dạng 3: Toán có lời văn.

Phương pháp:

Bước 1: Đọc và tìm hiểu đề bài.

Bước 2: Tìm cách giải.

Bước 3: Trình bày bài giải và kiểm tra kết quả vừa tìm được.

Ví dụ 1: Một mảnh vườn có $\frac{7}{8}$ diện tích đã trồng hoa và cây xanh, trong đó $\frac{2}{5}$ diện tích của mảnh vườn đã trồng hoa. Hỏi diện tích để trồng cây xanh là bao nhiêu phần diện tích của mảnh vườn?

Lời giải:

Số phần diện tích trồng cây xanh so với mảnh vườn là:

$\frac{7}{8}-\frac{2}{5}= \frac{35}{40}-\frac{16}{40}=\frac{19}{40}$

Đáp số:$\frac{19}{40}$

Ví dụ 2: Trong một ngày, thời gian để học toán và học tiếng anh của Minh là $\frac{5}{2}$  giờ, trong đó thời gian học toán của Minh là $\frac{3}{2}$ giờ. Hỏi thời gian học tiếng anh của Minh là bao nhiêu?

Lời giải:

Thời gian học tiếng anh của Minh là:

$\frac{5}{2}-\frac{3}{2}=\frac{2}{2}=1$ ( giờ)

Đáp số: 1 giờ.

Bài tập vận dụng (có đáp án)

Bài 1 :

Tính:

a) 

b)

c) 

d)

Phương pháp giải:

Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số. Nếu phân số thu được có thể rút gọn được thì ta rút gọn thành phân số tối giản.

a) 

b) 

c) 

d)

Bài 2 :

Rút gọn rồi tính

a) 

b) 

Phương pháp giải:

– Rút gọn các phân số thành phân số tối giản (nếu được), sau đó thực hiện phép trừ hai phân số.

– Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số.

Đáp án

a) 

b) 

Bài 3 :

Tính rồi rút gọn

a)

b) 

c) 

Phương pháp giải:

Muốn trừ hai phân số cùng mẫu số, ta trừ tử số của phân số thứ nhất cho tử số của phân số thứ hai và giữ nguyên mẫu số. Nếu phân số thu được có thể rút gọn được thì ta rút gọn thành phân số tối giản.

Đáp án

a) 

b) 

c) 

Bài 4 :

Hưởng ứng đợt tiêm chủng cho trẻ em, xã Hòa Bình ngày thứ nhất có 8/23 số trẻ em trong xã đã đi tiêm chủng, ngày thứ hai có 11/23 số trẻ em trong xã đi tiêm chủng. Hỏi ngày thứ hai số trẻ em đã đi tiêm chủng nhiều hơn ngày thứ nhất bao nhiêu phần của số trẻ em trong xã.

Phương pháp giải:

Số trẻ em ngày thứ hai đi tiêm chủng nhiều hơn ngày thứ nhất = số trẻ em đi tiêm chủng trong ngày thứ hai – số trẻ em đi tiêm chủng ngày thứ nhất.

Tóm tắt

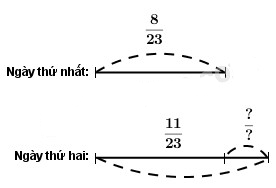
Bài giải

Số trẻ em ngày thứ hai tiêm nhiều hơn ngày thứ nhất là:

(số trẻ em)

Đáp số: số trẻ em.

Bài 5:

a) Muốn trừ hai phân số có cùng mẫu số thì?

b) Trà nói rằng: “Muốn trừ hai phân số khác mẫu số thì ta lấy tử số trừ cho nhau, mẫu số giữ nguyên”. Bạn Trà nói như vậy là đúng hay sai?

Bài giải:

a) Muốn trừ hai phân số có cùng mẫu số thì ta lấy tử số trừ cho nhau, mẫu số giữ nguyên.

b, Bạn Trà nói như vậy là sai. Muốn trừ hai phân số khác mẫu thì ta phải quy đồng mẫu số hai phân số rồi mới trừ hai phân số đó.

Bài 6: Tìm x biết: .

Bài giải:

.

Bài 7: Tính

a) 

b) 

Bài giải:

a) 

b) 

Xem thêm các dạng bài tập liên quan khác:

50 Bài tập về Phân số bằng nhau.Rút gọn phân số (có đá án năm 2023)

50 Bài tập về Phép chia phân số (Có đáp án năm 2023)

60 Bài tập về Phép cộng phân số (có đáp án năm 2023)

60 Bài tập về Phép nhân phân số (có đáp án năm 2023)

60 Bài tập về Phép trừ phân số (có đáp án năm 2023)