50 Bài tập về Phân số bằng nhau.Rút gọn phân số (có đáp án năm 2024) - Toán lớp 4

Bài tập về Phân số bằng nhau. Rút gọn phân số

Kiến thức cần nhớ

Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.

Khi rút gọn phân số có thể làm như sau:

Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Ví dụ: Rút gọn phân số$\frac{6}{9}$.

Ta thấy 6 và 9 đều chia hết cho 3 nên:

$\frac{6}{9}=\frac{6:3}{9:3}= \frac{2}{3}$.

2 và 3 không cùng chia hết cho một số tự nhiên nào lớn hơn 1 nên phân số $\frac{2}{3}$  không thể rút gọn được nữa. Ta nói rằng phân số $\frac{2}{3}$ là phân số tối giản và phân số $\frac{6}{9}$ đã được rút gọn thành phân số tối giản $\frac{2}{3}$ .

Các dạng bài tập về Phân số bằng nhau. Rút gọn phân số

Dạng 1: Tìm phân số bằng nhau

Phương pháp:

Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.

Ví dụ: Phân số nào dưới đây bằng với phân số $\frac{3}{4}$ ?

A.$\frac{9}{12}$

B. $\frac{15}{12}$

C. $\frac{7}{8}$

Lời giải:

Ta có:

$\frac{9}{12}= \frac{9:3}{12:3}=\frac{3}{4}$; $\frac{15}{12}= \frac{15:3}{12:3}= \frac{5}{4}$

Vậy trong các phân số đã cho, phân số bằng phân số $\frac{3}{4}$ là  $\frac{9}{12}$.

Dạng 2: Rút gọn phân số

Phương pháp:

Khi rút gọn phân số có thể làm như sau:

Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Ví dụ: Rút gọn các phân số: $\frac{8}{16};\frac{15}{40};\frac{75}{36}$ .

Lời giải:

Ta thấy cả 8 và 16 đều chia hết cho 8 nên:$\frac{8}{16}=\frac{8:8}{16:8}=\frac{1}{2}$ .

Ta thấy cả 15 và 40 đều chia hết cho 5 nên: $\frac{15}{40}=\frac{15:5}{40:5}=\frac{3}{8}$ .

Ta thấy cả 75 và 36 đều chia hết cho 3 nên:$\frac{75}{36}= \frac{75:3}{36:3}=\frac{25}{12}$ .

Dạng 3: Tìm phân số tối giản

Phương pháp:

Phân số tối giản có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1.

Ví dụ: Trong các phân số sau đây: $\frac{5}{6};\frac{4}{7};\frac{30}{42};\frac{7}{21}$.

Phân số nào là phân số tối giản, phân số nào không là phân số tối giản? Nếu phân số đã cho không là phân số tối giản thì hãy rút gọn phân số đó.

Lời giải:

Phân số $\frac{5}{6}$ : Ta thấy 5 và 6 không cùng chia hết cho một số tự nhiên nào lớn hơn 1 nên phân số $\frac{5}{6}$ là phân số tối giản.

Phân số $\frac{4}{7}$ : Ta thấy 4 và 7 không cùng chia hết cho một số tự nhiên nào lớn hơn 1 nên phân số  là phân số $\frac{4}{7}$ tối giản.

Phân số $\frac{30}{42}$ : Ta thấy 30 và 42 đều chia hết cho 6 nên: $\frac{30}{42}= \frac{30:6}{42:6}= \frac{5}{7}$ .

Phân số $\frac{7}{21}$ : Ta thấy 7 và 21 đều chia hết cho 7 nên: $\frac{7}{21}=\frac{7:7}{21:7}=\frac{1}{3}$.

Bài tập tự luyện (có đáp án)

Bài tập tự luyện số 1

Bài 1: Viết số thích hợp vào chỗ trống:

a,

$$\begin{gathered} \frac{280}{49}=\frac{280:\mathrm{...}}{49:\mathrm{...}}=\frac{\mathrm{...}}{\mathrm{...}}; \\ \frac{144}{240}=\frac{144:\mathrm{...}}{\mathrm{...}:12}=\frac{\mathrm{...}}{20}; \\ \frac{225}{450}=\frac{225:\mathrm{...}}{450:\mathrm{...}}=\frac{\mathrm{...}}{\mathrm{...}} \end{gathered}$$

b,

$$\begin{gathered} \frac{7}{8}=\frac{7\times 6}{8\times 6}=\frac{\mathrm{...}}{\mathrm{...}}; \\ \frac{10}{11}=\frac{10\times \mathrm{...}}{11\times 10}=\frac{\mathrm{...}}{\mathrm{...}}; \\ \frac{25}{37}=\frac{25\times 5}{37\times \mathrm{...}}=\frac{\mathrm{...}}{\mathrm{...}} \end{gathered}$$

Bài 2: Viết số thích hợp vào ô trống:

$$\begin{gathered} \frac{450}{\mathrm{...}}=\frac{50}{10}=\mathrm{...};\frac{6}{7}=\frac{\mathrm{...}}{42}; \\ \frac{120}{\mathrm{...}}=\frac{20}{70}=\frac{\mathrm{...}}{7};\frac{\mathrm{...}}{7}=\frac{12}{28}=\frac{120}{\mathrm{...}} \end{gathered}$$

Bài 3: Tìm các phân số bằng nhau ở từng nhóm sau:

a, $\frac{1}{2};\frac{2}{4};\frac{5}{8};\frac{4}{8};\frac{9}{10};\frac{3}{6}$

b, $\frac{1}{4};\frac{2}{9};\frac{2}{8};\frac{3}{12};\frac{5}{16};\frac{5}{20}$

c, $\frac{2}{5};\frac{14}{15};\frac{8}{20};\frac{8}{25};\frac{10}{25};\frac{12}{20}$

Bài 4: Viết phân số

a) Viết 4 phân số bằng phân số $\frac{3}{4}$.

b) Viết 4 phân số bằng phân số $\frac{7}{9}$.

Bài 5: Trong các nhóm 2 phân số dưới đây, nhóm nào có 2 phân số bằng nhau?

a) $\frac{5}{6}$ và $\frac{15}{24}$

b) $\frac{3}{5}$ và $\frac{21}{35}$

c) $\frac{8}{12}$ và $\frac{2}{3}$

d) $\frac{3}{7}$ và $\frac{15}{28}$

e) $\frac{9}{27}$ và $\frac{1}{3}$

Bài 6: Ban đầu cái bánh được cắt thành 4 phần bằng nhau, Tuấn ăn 1 phần. Hỏi nếu cái bánh được cắt thành 12 phần bằng nhau thì Tuấn đã ăn bao nhiêu phần cái bánh?

Bài 7: Có ba cái bánh như sau:

Một cái bánh được cắt thành 3 phần, em ăn 1 phần.

Một cái bánh được cắt thành 5 phần, em ăn 1 phần.

Một cái bánh được cắt thành 6 phần, em ăn 1 phần.

Hỏi em ăn phần bánh nào được nhiều nhất, phần bánh nào được ít nhất?

Bài 8: Tìm phân số bằng phân số $\frac{1}{2}$ mà tử số bé hơn mẫu số 127 đơn vị.

Bài 9: Có bao nhiêu phân số bằng $\frac{3}{4}$ mà tử số nhỏ hơn 20.

Bài 10: Tìm phân số bằng $\frac{3}{5}$ mà mẫu số của nó là số liền sau số lớn nhất có hai chữ số.

Bài 11: Tìm phân số bằng $\frac{3}{5}$ mà mẫu số lớn hơn tử số 8 đơn vị.

Bài 12: Tìm các phân số bằng nhau trong các phân số dưới đây:

a, 

b, 

c, 

Bài 13:

a, Viết năm phân số bằng phân số 

b, Viết năm phân số bằng phân số 

Bài 14: Điền số thích hợp vào chỗ chấm:

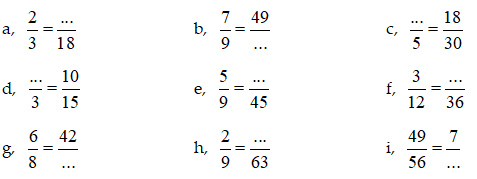
Bài 15: Trong các nhóm hai phân số dưới đây, nhóm nào có hai phân số bằng nhau?

a, b,  c,

d,  e, f,

Bài 16: Trong các hình dưới đây, hai hình nào có các phân số chỉ phần tô đậm là hai phân số bằng nhau ?

A. (1) và (2)

B. (1) và (4)

C. (2) và (3)

D. (3) và (4)

Bài tập tự luyện số 2

Bài 1: Rút gọn các phân số: $\frac{25}{50};\frac{15}{120};\frac{64}{720};\frac{5}{25}$

Bài 2: Viết số thích hợp vào chỗ trống: $\frac{160}{320}=\frac{16}{\mathrm{...}}=\frac{\mathrm{...}}{16}=\frac{4}{\mathrm{...}}=\frac{1}{2}$

Bài 3: Tính nhanh

a, $\frac{5\times 7\times 8\times 9\times 10}{7\times 8\times 9\times 10\times 11}$

b, $\frac{3\times 145+3\times 55}{6\times 215+6\times 85}$

Bài 4: Trong các phân số sau, phân số nào là phân số tối giản. Phân số nào chưa tối giản em hãy rút gọn.

$\frac{9}{10};\frac{15}{18};\frac{21}{15};\frac{5}{4};\frac{16}{4};\frac{256}{112}$

Bài 5: Rút gọn phân số: $\frac{25\times 8+25\times 9+25-25\times 5}{99+98+97+96}$

Bài 6: Rút gọn các phân số dưới đây thành phân số tối giản.

a, $\frac{6}{9};\frac{6}{24};\frac{48}{96};\frac{42}{98}$

b, $\frac{24}{36};\frac{18}{30};\frac{15}{120};\frac{80}{240}$

c, $\frac{5}{25};\frac{75}{100};\frac{64}{720};\frac{16}{1000}$

Bài 7: Tìm phân số tối giản trong các phân số sau:

$\frac{4}{16};\frac{2}{5};\frac{15}{24};\frac{7}{12};\frac{16}{18};\frac{49}{50}$

Bài 8: Hãy tìm 1 số tự nhiên, biết rằng sau khi chia cả tử số và mẫu số của phân số $\frac{47}{56}$ cho số đó ta được phân số $\frac{7}{8}$.

Bài 9: Tính giá trị của biểu thức sau: $A=\frac{3\times 7\times 8}{7\times 8\times 9}$

Bài 10: Tìm x, biết: $\frac{x+1}{3}=\frac{16}{24}$

Bài 11: Rút gọn các phân số sau:

$\frac{3131}{3535};\frac{204204}{217217};\frac{414141}{494949};\frac{171171171}{180180180}$

Bài 12: Rút gọn các phân số sau thành phân số tối giản:

$\frac{18}{45};\frac{35}{84};\frac{72}{120};\frac{36}{108};\frac{75}{145};\frac{100}{175}$

Bài 13: Rút gọn các phân số sau về phân số tối giản:

a) 

b) 

Bài 14: Tìm phân số có tổng tử số và mẫu số bằng 256 và sau khi rút gọn phân số ta được phân số tối giản là 

Bài tập tự luyện số 3

Bài 1: Tìm các phân số tối giản trong các phân số sau:

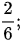
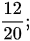
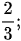
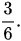
Bài giải:

Phân số tối giản là: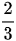 

Bài 2: Rút gọn phân số: 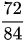 để phân số sau trở thành phân số tối giản:

Bài giải:

Ta thấy phân số 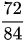 có tử và mẫu đều chia hết cho 4:

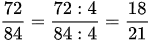
Ta thấy phân số 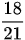 có tử và mẫu đều chia hết cho 3:

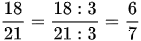
Vậy 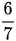 là phân số tối giản của phân số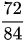 

Bài 3: Điền số thích hợp vào chỗ trống 

Bài giải:

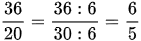
Bài tập tự luyện số 4

Bài 1 : Phân số nào chưa tối giản ?

A. 2/3 

B. 4/5

C. 3/9

D. 2/7

Bài 2 : Rút gọn các phân số:

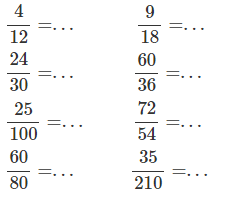
Phương pháp giải:

Cách rút gọn phân số:

– Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn một

– Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).

Đáp án

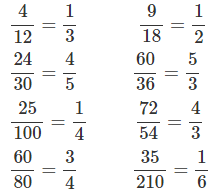
Bài 3 : Khoanh vào những phân số bằng 

Phương pháp giải:

Rút gọn các phân số đã cho, phân số bằng phân số  thì rút gọn được thành phân số tối giản là .

Đáp án

Ta có :

Phân số  có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1 nên là phân số tối giản.

Vậy ta có kết quả như sau:

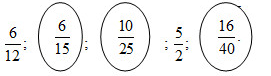
Xem thêm các dạng bài tập liên quan khác:

50 Bài tập về Phân số bằng nhau.Rút gọn phân số (có đá án năm 2023)

50 Bài tập về Phép chia phân số (Có đáp án năm 2023)

60 Bài tập về Phép cộng phân số (có đáp án năm 2023)

60 Bài tập về Phép nhân phân số (có đáp án năm 2023)

60 Bài tập về Phép trừ phân số (có đáp án năm 2023)