Đạo hàm
Kiến thức cần nhớ
I. Đạo hàm tại một điểm
1. Định nghĩa đạo hàm tại một điểm
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 thuộc (a; b). Nếu tồn tại giới hạn (hữu hạn) : thì giới hạn đó được gọi là đạo hàm của hàm số y= f(x) tại điểm x0 và được kí hiệu là f'(x0). Vậy
* Chú ý:
Đại lượng ∆x = x- x0 được gọi là số gia của đối số tại x0.
Đại lượng ∆y= f(x) – f(x0)= f(x0 + ∆x) – f(x0) được gọi là số gia tương ứng của hàm số. Như vậy: .
2. Quy tắc tính đạo hàm bằng định nghĩa:
Để tính đạo hàm của hàm số y = f(x) tại điểm x0 bằng định nghĩa, ta có quy tắc sau đây:
+ Bước 1: Giả sử ∆x là số gia của đối số tại x0 tính:
∆y= f(x0 + ∆x) – f( x0) .
+ Bước 2: Lập tỉ số .
+ Bước 3: Tìm
Ví dụ 1. Cho hàm số , có là số gia của đối số tại x = 2. Khi đó bằng bao nhiêu.
Lời giải
Tập xác định của hàm số đã cho là: .
Giả sử ∆x là số gia của đối số tại x0 = 2. Ta có:
Khi đó:
Vậy f’(2) = 1.
3. Quan hệ giữa sự tồn tại của đạo hàm và tính liên tục của hàm số
Định lý 1. Nếu hàm số y= f( x) có đạo hàm tại x0 thì nó liên tục tại điểm đó.
Chú ý:
+ Nếu hàm số y= f(x) gián đoạn tại x0 thì hàm số không có đạo hàm tại điểm đó.
+ Một hàm số liên tục tại một điểm có thể không có đạo hàm tại điểm đó.
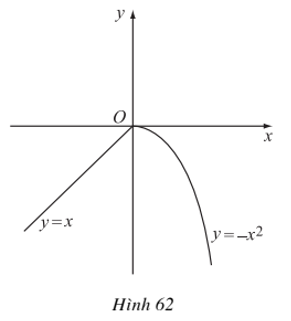
Ví dụ 2. Chẳng hạn hàm số liên tục tại x = 0 nhưng không có đạo hàm tại đó. Ta nhận xét rằng đồ thị của hàm số này là một đường liền, nhưng bị gãy tại điểm O(0;0) như hình vẽ sau:
4. Ý nghĩa của đạo hàm
a) Ý nghĩa hình học của đạo hàm:
+) Định lí: Đạo hàm của hàm số y= f(x) tại điểm x = x0 là hệ số góc của tiếp tuyến M0T của đồ thị hàm số y= f( x) tại điểm M0(x0; f(x0)).
+) Định lí: Phương trình tiếp tuyến của đồ thị hàm số y = f(x) tại điểm M0(x0; f(x0)) là:
y – y0= f’(x0) ( x- x0) trong đó y0= f(x0).
Ví dụ 3. Viết phương trình tiếp tuyến của đường cong y = x3 – 3x2 + 2 tại điểm có hoành độ x = 3.
Lời giải
Bằng định nghĩa ta tính được: y’(3) = 9.
Do đó hệ số góc của tiếp tuyến là 9.
Ta có: y(3) = 2.
Vậy phương trình tiếp tuyến của đường cong tại điểm có hoành độ x = 3 là:
y = 9(x – 3) + 2 = 9x – 27 + 2 = 9x – 25.
b) Ý nghĩa vật lý của đạo hàm:
+) Vận tốc tức thời:
Xét chuyển động thẳng xác định bởi phương trình: s= s(t); với s= s(t) là một hàm số có đạo hàm. Vận tốc tức thời tại thời điểm t0 là đạo hàm của hàm số s= s(t) tại t0: v(t0) = s’(t0).
+) Cường độ tức thời:
Nếu điện lượng Q truyền trong dây dẫn là một hàm số của thời gian: Q= Q(t) ( là hàm số có đạo hàm) thì cường độ tức thời của dòng điện tại thời điểm t0 là đạo hàm của hàm số Q= Q(t) tại t0: I(t0) = Q’(t0) .
Ví dụ 4. Một xe máy chuyển động theo phương trình : s(t)= t2 + 6t+ 10 trong đó t đơn vị là giây; s là quãng đường đi được đơn vị m. Tính vận tốc tức thời của xe tại thời điểm t= 3.
Lời giải
Phương trình vận tốc của xe là v( t)=s' ( t)=2t+6 ( m/s)
⇒ Vận tốc tức thời của xe tại thời điểm t= 3 là:
V(3)= 2.3+ 6 = 12 (m/s)
Chọn A.
II. Đạo hàm trên một khoảng
Hàm số y = f(x) được gọi là có đạo hàm trên khoảng (a; b) nếu nó có đạo hàm tại mọi điểm x trên khoảng đó.
Khi đó ta gọi hàm số f’:
là đạo hàm của hàm số y = f(x) trên khoảng (a;b), kí hiệu là y’ hay f’(x).
Ví dụ 5. Hàm số y = x2 – 2x có đạo hàm y’ = 2x – 2 trên khoảng .
Hàm số có đạo hàm trên các khoảng và .
III. Đạo hàm của một hàm số thường gặp
1. Định lý 1
Hàm số y = xn có đạo hàm tại mọi và (xn)’ = n.xn-1.
2. Định lý 2
Hàm số có đạo hàm tại mọi x dương và .
Ví dụ 1.
a) Tính đạo hàm y = x3;
b) Tính đạo hàm tại x = 5.
Lời giải
a) Ta có: y’ = 3x2;
b) Ta có:
Đạo hàm của hàm số tại x = 5 là:
IV. Đạo hàm của tổng, hiệu, tích, thương
1. Định lí 3
Giả sử u = u(x), v = v(x) là các hàm số có đạo hàm tại điểm x thuộc khoảng xác định, ta có:
(u + v)’ = u’ + v’;
(u – v)’ = u’ – v’;
(uv)’ = u’.v + u.v’;
.
2. Hệ quả
Hệ quả 1. Nếu k là một hằng số thì (ku)’ = k.u’.
Hệ quả 2.
Ví dụ 2. Tính đạo hàm của các hàm số sau:
a) y = x5 – 2x2 + 3x + 6;
b) y = (x2 + 1)(2x – 3);
c) .
Lời giải
a) y = x5 – 2x2 + 3x
y’ = (x5 – 2x2 + 3x)’
= (x5)’ – (2x2)’ + (3x)’
= 5x4 – 4x + 3.
b) y = (x2 + x).2x
y’ = (x2 + x)’.2x + (x2 + 1)(2x)’
= [(x2)’ + x’].2x + (x2 + 1).2
= (2x + 1).2x + 2x2 + 2
= 4x2 + 2x + 2x2 + 2
= 6x2 + 2x + 2.
c)
V. Đạo hàm hàm hợp
Định lý 4. Nếu hàm số u = g(x) có đạo hàm x là và hàm số y = f(u) có đạo hàm tại u là thì hàm hợp y = f(g(x)) có đạo hàm tại x là: .
Ví dụ 3. Tính đạo hàm của hàm số:
Lời giải
Đặt thì
.
VI. Đạo hàm hàm lượng giác
1. Giới hạn
Định lý 1.
Ví dụ 1. Tính
Lời giải
Đặt x – 1 = t.
Khi x tiến đến 1 thì t tiến đến 0.
2. Đạo hàm của hàm số y = sinx
Định lý 2.
Hàm số y = sinx có đạo hàm tại mọi và (sinx)’ = cosx.
Chú ý:
Nếu y = sinu và u = u(x) thì: (sinu)’ = u’.cosu
Ví dụ 2. Tính đạo hàm của hàm số
Lời giải
3. Đạo hàm của hàm số y = cosx
Định lý 3.
Hàm số y = cosx có đạo hàm tại mọi và (cosx)’ = - sinx.
Chú ý:
Nếu y = cosu và u = u(x) thì: (cosu)’ = - u’.sinu
Ví dụ 3. Tính đạo hàm của hàm số tại .
Lời giải
Đặt
Thay vào y’ ta được:
Vậy giá trị của đạo hàm của hàm số tại là
4. Đạo hàm của hàm số y = tanx
Định lý 4.
Hàm số y = tanx có đạo hàm tại mọi và (tanx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (tanu)’ =
Ví dụ 4. Tính đạo hàm
Lời giải
Đặt u = 2 + tanx
5. Đạo hàm của hàm số y = cotx
Định lý 5.
Hàm số y = cotx có đạo hàm tại mọi và (cotx)’ = .
Chú ý:
Nếu y = u và u = u(x) thì: (cotu)’ =
Ví dụ 5. Tính đạo hàm của hàm y = cot x2.
Lời giải
y’ = (cot x2)’ = (x2)’.=.
6. Bảng quy tắc tính đạo hàm tổng hợp:

VII. Đạo hàm cấp hai
1. Định nghĩa
Giả sử hàm số y = f(x) có đạo hàm tại mỗi điểm x ∈ (a;b). Khi đó, hệ thức y’ = f’(x) xác định một hàm số mới trên khoảng (a; b). Nếu hàm số y’ = f’(x) lại có đạo hàm tại x thì ta gọi đạo hàm của y’ là đạo hàm cấp hai của hàm số y = f(x) và kí hiệu là y” hoặc f”(x).
Chú ý:
+ Đạo hàm cấp 3 của hàm số y = f(x) được định nghĩa tương tự và kí hiệu là y”’ hoặc f”’(x) hoặc f(3)(x).
+ Cho hàm số y = f(x) có đạo hàm cấp n – 1 , kí hiệu f(n–1)(x) (n ∈ N, n ≥ 4). Nếu f(n–1)(x) có đạo hàm thì đạo hàm của nó được gọi là đạo hàm cấp n của f(x), kí hiệu y(n) hoặc f(n)(x).
f(n)(x) = (f(n–1)(x))’.
Ví dụ 1. Với y = 7x4 + 8x + 12. Tính y(5)
Lời giải
Ta có: y’ = 28x3 + 8, y” = 84x2, y”’ = 168x, y(4) = 168, y(5) = 0.
Vậy y(5) = 0.
2. Ý nghĩa cơ học của đạo hàm cấp hai
Xét chuyển động xác định bởi phương trình s = f(t), trong đó s = f(t) là một hàm số có đạo hàm đến cấp hai. Vận tốc tức thời tại t của chuyển động là v(t) = f’(t).
Lấy số gia tại t thì v(t) có số gia tương ứng là
Tỉ số được gọi là gia tốc trung bình của chuyển động trong khoảng thời gian . Nếu tồn tại: .
Ta gọi là gia tốc tức thời của chuyển động tại thời điểm t.
Vì v(t) = f’(t) nên: .
Đạo hàm cấp hai f”(t) là gia tốc tức thời của chuyển động s = f(t) tại thời điểm t.
Ví dụ 2. Tính gia tốc tức thời của sự rơi tự do
Lời giải
Ta có:
Gia tốc tức thời của sự tơi tự do là: .
Vậy gia tốc tức thời của sự rơi tự do là:
Bài tập tự luyện
1. Bài tập vận dụng
Bài 1. Cho hàm số: (C)
a) Hãy tính đạo hàm bằng định nghĩa của hàm số đã cho tại x = 1.
b) Viết phương trình tiếp tuyến của hàm số (C) tại điểm A(1;-2).
Lời giải
a) Tập xác định của hàm số đã cho là: .
Giả sử ∆x là số gia của đối số tại x0 = 1. Ta có:
Khi đó:
Vậy f’(1) = - 5.
b) Bằng định nghĩa ta tính được: y’(1) = -5.
Do đó hệ số góc của tiếp tuyến là -5.
Ta có: y(1) = - 2.
Vậy phương trình tiếp tuyến của đường cong tại điểm A(1;-2) là:
y = -5(x – 1) - 2 = -5x + 5 - 2 = -5x + 3.
Bài 2. Chứng minh rằng hàm số không có đạo hàm tại x = 0 nhưng liên tục tại điểm đó.
Lời giải
Ta có f(0) = 1.
Trước hết, ta tính giới hạn bên phải của tỉ số . Ta có:
Giới hạn bên trái của tỉ số , ta có:
Vì giới hạn hai bên khác nhau nên không tồn tại . Điều này chứng tỏ hàm số không có đạo hàm tại điểm x = 0.
Ta có:
Do đó hàm số liên tục tại x = 1.
Vậy hàm số liên tục tại x = 1 nhưng không có đạo hàm tại x = 1.
Bài 3. Cho biết điện lượng truyền trong dây dẫn theo thời gian biểu thị bởi hàm số Q(t) = 2t2 + t, trong đó t được tính bằng giây (s) và Q được tính theo Culong (C). Tính cường độ dòng điện tại thời điểm t = 4s.
Lời giải
Cường độ dòng điện tại t = 4 là: I(4) = Q’(4).
Đạo hàm của hàm Q(t) tại t = 4 bằng 17.
Vậy cường độ dòng điện tại t = 4 là 17 A.
Bài 4. Viết phương trình tiếp tuyến của đồ thị của các hàm số:
a) , biết hệ số góc của tiếp tuyến là ;
b) y = x3 + 2x tại điểm có hoành độ bằng 2.
Lời giải
a)
Vậy phương trình tiếp tuyến của đồ thị của hàm số đã cho là:
b)
Ta có y(2) = 12.
Phương trình tiếp tuyến của đồ thị hàm số đã cho là:
y = 14(x – 2) + 12 = 14x – 28 + 12 = 14x – 16.
Vậy phương trình tiếp tuyến của đồ thị hàm số đã cho là y = 14x – 16.
Bài 5. Tính đạo hàm các hàm số sau:
1.
2.
3.
4.
5.
6.
Lời giải
1. Ta có:
2. Ta có:
3. Ta có:
4. Ta có:
5. Ta có:
6. Ta có:
Bài 6. Tính đạo hàm các hàm số sau:
a)
b)
Lời giải
a) Đặt u = (x7 + x)2
b) Đặt u = 2x2 + 3x + 1
Bài 7. Cho và . Giải bất phương trình f’(x) > g’(x).
Lời giải
Ta có:
Xét bất phương trình: f’(x) > g’(x)
Vậy tập nghiệm của bất phương trình là: .
Bài 8. Cho f(x) = x5 + x3 – 2x – 3. Chứng minh rằng:
f’(1) + f’(-1) = -4f(0).
Lời giải
Ta có: f’(x) = (x5 + x3 – 2x – 3)’ = 5x4 + 3x2 – 2.
Khi đó:
f’(1) = 5.14 + 3.12 – 2 = 5 + 3 – 2 = 6.
f’(-1) = 5.(-1)4 + 3.(-1)2 – 2 = 5 + 3 – 2 = 6.
f(0) = 05 + 03 – 2.0 – 3 = 0 + 0 – 0 – 3 = - 3.
f’(1) + f’(-1) = 6 + 6 = 12 và -4f(0) = -4.(-3) = 12.
Vậy f’(1) + f’(-1) = -4f(0).
Bài 9. Tính các đạo hàm sau:
a)
b)
c)
d)
Lời giải
a)
b)
c)
d)
Bài 10. Chứng minh rằng các hàm số sau đây có đạo hàm không phụ thuộc x.
a)
b)
Lời giải
a)
b)
Bài 11. Tìm f’(2) biết f(x) = x2.sin(x – 2).
Lời giải
Ta có : f’(x) = 2x.sin(x – 2) + x2cos(x – 2)
Khi đó: f’(2) = 2.2.sin(2 – 2) + 22.cos(2 – 2)
= 4.0 + 4.1
= 0 + 4
= 4.
Vậy f’(2) = 4.
Bài 12: Tính đạp hàm cấp hai của các hàm số sau:
a) y = sin5x.cos2x;
b) ;
c) y = (1 – x2)cosx;
d) y = .
Lời giải
a) y’ = (sin5x.cos2x)’ = 5cos5x.cos2x – 2sin5x.sin2x
y” = (5cos5x.cos2x – 2sin5x.sin2x)’
= - 25sin5x.cos2x – 10cos5xsin2x – 10cos5xsin2x – 4sin5x.cos2x.
b)
c) y’ = [(1 – x2)cosx]’ = -2x.cosx – (1- x2).sinx
y” = [-2x.cosx – (1- x2).sinx]’ = -2cosx + 2xsinx + 2xsinx – (1 – x2).cosx.
d)
Bài 13. Cho hàm số y = (3x – 4)6. Tính y”(2) và y(4)(2).
Lời giải
Ta có: y’ = 6(3x – 4)5.3 = 18(3x – 4)5
Khi đó, ta có:
Vậy y”(2) = 4320 và y(4)(2) = 116640.
2. Bài tập tự luyện có hướng dẫn
Xem thêm các dạng bài tập liên quan khác:
70 Bài tập về đạo hàm của hàm số lượng giác (có đáp án năm 2023)
500 Bài tập Toán 11 chương 5: Đạo hàm (có đáp án năm 2023)
70 Bài tập về phép biến hình (có đáp án năm 2023)
70 Bài tập về phép tịnh tiến (có đáp án năm 2023)
70 Bài tập về phép đối xứng trục (có đáp án năm 2023)












