Bài giảng Toán 11 Bài 2: Phép tịnh tiến
Kiến thức cần nhớ
I. Định nghĩa.
- Định nghĩa: Trong mặt phẳng, cho vectơ →v. Phép biến hình biến mỗi điểm M thành điểm M’ sao cho →MM' = →v được gọi là phép tịnh tiến theo vectơ →v.
- Phép tịnh tiến theo vectơ thường được kí hiệu là được gọi là vectơ tịnh tiến.
Vậy: T→v (M)= M' ⇔→MM' = →v.
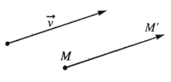
- Phép tịnh tiến theo vectơ – không chính là phép đồng nhất.
- Ví dụ 1. Cho hình vẽ sau:
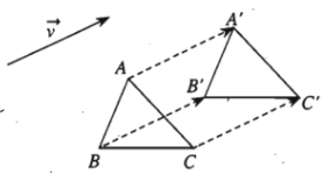
Ta có: T→v (A)= A' ; T→v (B)= B' ; T→v (C)= C' .
II. Tính chất
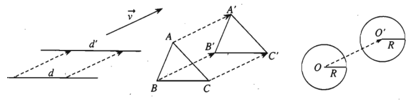
- Tính chất 1. Nếu T→v (M)= M' ; T→v (N)= N' thì →M'N' = →MN và từ đó suy ra M’N’ = MN.
Phép tịnh tiến bảo toàn khoảng cách giữa hai điểm bất kì.
- Tính chất 2. Phép tịnh tiến biến đường thẳng thành đường thẳng song song hoặc trùng với nó, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.
III. Biểu thức tọa độ.
Trong mặt phẳng tọa độ Oxy cho vectơ →v (a ; b). Với mỗi điểm M(x ; y) ta có M’(x’ ; y’) là ảnh của điểm M qua tịnh tiến theo vectơ →v.
Khi đó:
→MM' = →v ⇔{x'−x =ay' − y=b ⇒{x'=x +ay' = y+b
đây chính là biểu thức tọa độ của phép tịnh tiến T→v.
Ví dụ 2. Trong mặt phẳng tọa độ Oxy, cho điểm A(1 ; – 2). Phép tịnh tiến theo vectơ biến A thành điểm A’ có tọa độ là bao nhiêu?
Lời giải:
Gọi tọa độ điểm A’ = (x’; y’).
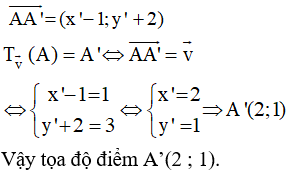
Các dạng toán về phép tịnh tiến
Dạng toán 1. Xác định ảnh của một hình qua phép tịnh tiến
Phương pháp: Sử dụng định nghĩa và các tính chất hoặc biểu thức tọa độ của phép tịnh tiến.
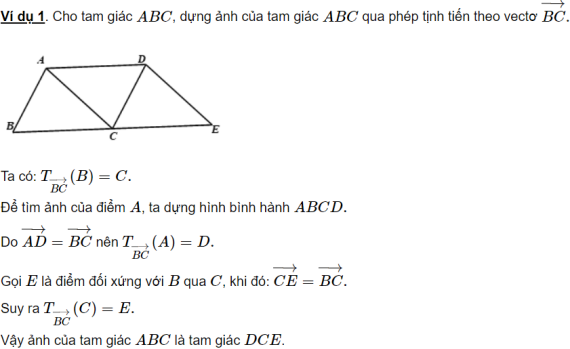
Dạng toán 2. Xác định phép tịnh tiến khi biết ảnh và tạo ảnh
Phương pháp: Xác định phép tịnh tiến tức là tìm tọa độ của →v. Để tìm tọa độ của →v ta có thể giả sử →v=(a;b), sử dụng các dữ kiện trong giả thiết của bài toán để thiết lập hệ phương trình hai ẩn a, b và giải hệ tìm a,b.

Dạng toán 3. Dùng phép tịnh tiến để giải các bài toán dựng hình
Phương pháp:
• Để dựng một điểm M ta tìm cách xem nó là ảnh của một điểm đã biết qua một phép tịnh tiến, hoặc xem M là giao điểm của hai đường trong đó một đường cố định còn một đường là ảnh của một đường đã biết qua phép tịnh tiến.
• Sử dụng kết quả: Nếu T→V(N)=M và N∈(H) thì M∈(H'), trong đó (H')=T→V((H)) và kết hợp với M thuộc hình (K) (theo giả thiết) để suy ra M∈(H')∩(K).

Dạng toán 4. Sử dụng phép tịnh tiến để giải các bài toán tìm tập hợp điểm
Phương pháp: Nếu T→V(M)=M' và đểm M di động trên hình (H) thì điểm M' thuộc hình (H'), trong đó (H') là ảnh của hình (H) qua T→V.

Bài tập tự luyện
1. Bài tập vận dụng
Bài 1. Cho phép tịnh tiến T→u biến điểm M thành M1 và phép tịnh tiến T→v biến M1 thành M2. Hỏi tịnh tiến theo vectơ (→u + →v) biến điểm M thành điểm nào?
Lời giải:
Theo giả thiết ta có:
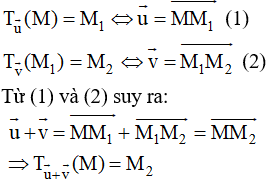
Vậy tịnh tiến theo vectơ(→u + →v) biến điểm M thành điểm M2.
Bài 2. Trong mặt phẳng tọa độ Oxy, cho 2 điểm A(2; 1); B(– 1; – 4). Gọi C và D lần lượt là ảnh của A và B qua phép tịnh tiến theo vectơ →v (1 ; 5). Tính độ dài đoạn thẳng CD?
Lời giải:
Ta có:
AB = √(−1 −2)2 + (−4−1)2 = √34
Vì T→v (A)= C; T→v (B)= D nên theo tính chất của phép tịnh tiến ta có:
CD = AB= √34
Vậy CD = √34.
Bài 3. Trong mặt phẳng tọa độ Oxy, cho →v (1 ; −3) và đường thẳng d có phương trình 2x – 3y + 5 = 0. Viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến T→v.
Lời giải:
Cách 1. Sử dụng biểu thức tọa độ của phép tịnh tiến.
Lấy điểm M(x ; y) tùy ý thuộc d, ta có: 2x – 3y + 5 = 0 (1)
Gọi :
M'(x';y')=T→v(M)⇒{x'=x+1y'=y−3⇔{x=x'−1y=y'+3
Thay vào (1) ta được phương trình:
2(x’ – 1) – 3(y’ + 3) + 5 = 0 hay 2x’ – 3y’ – 6 = 0.
Vậy ảnh của d là đường thẳng d’: 2x – 3y – 6 = 0.
Cách 2. Sử dụng tính chất của phép tịnh tiến
Do T→v (d)= d' nên d’ song song hoặc trùng với d.
Suy ra, phương trình đường thẳng d’ có dạng: 2x – 3y + c = 0 (2).
Lấy điểm M(– 1; 1) thuộc d.
Khi đó T→v (M)= M'(x'; y').
{x'=−1+1 =0y'=1−3 =−2 ⇒M'(0; −2)
Do M’ thuộc d’ nên thay tọa độ M’ vào d’ ta được:
2.0 – 3.(– 2) + c = 0 nên c = – 6.
Vậy ảnh của d là đường thẳng d’: 2x – 3y – 6 = 0.
Bài 4. Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình
x2 + y2 + 2x – 4y – 4 = 0. Tìm ảnh của (C) qua phép tịnh tiến theo vectơ →v(1 ; 1).
Lời giải:
Sử dụng tính chất của phép tịnh tiến:
Đường tròn (C) có tâm I(–1 ; 2) và bán kính R = √(−1)2+ 22−(−4) = 3.
Gọi ảnh của (C) qua phép tịnh tiến theo vectơ là (C’) có tâm I’(x’; y’) và bán kính R’ = R = 3.
Ta tìm tâm I’(x’; y’).
Ta có:
{x' = −1 + 1=0y'= 2 + 1= 3 ⇒ I' (0; 3)
Do đó, phương trình của đường tròn (C’) là x2 + (y – 3)2 = 9.
2. Bài tập tự luyện có hướng dẫn
Xem thêm các dạng bài tập liên quan khác:
70 Bài tập về phép biến hình (có đáp án năm 2023)
70 Bài tập về phép tịnh tiến (có đáp án năm 2023)
70 Bài tập về phép đối xứng trục (có đáp án năm 2023)












