70 Bài tập về phép đối xứng trục (có đáp án năm 2023) - Toán 11

Bài giảng Toán 11 Bài 3: Phép đối xứng trục

Kiến thức cần nhớ

I. Định nghĩa.

- Cho đường thẳng d. Phép biến hình biến mỗi điểm M thuộc d thành chính nó, biến mỗi điểm M không thuộc d thành điểm M’ sao cho d là đường trung trực của đoạn MM’ được gọi là phép đối xứng qua đường thẳng d hay phép đối xứng trục d.

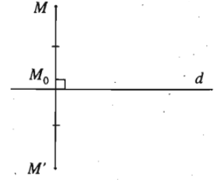
Đường thẳng d được gọi là trục của phép đối xứng hoặc đơn giản là trục đối xứng.

Phép đối xứng trục d thường được kí hiệu là Đ_d.

- Nếu hình ℋ ' là ảnh của hình ℋ  qua phép đối xứng trục d thì ta còn nói ℋ  đối xứng với ℋ ' qua d, hay ℋ  và ℋ ' đối xứng với nhau qua d.

- Nhận xét:

1) Cho đường thẳng d. Với mỗi điểm M, gọi M₀ là hình chiếu vuông góc của M

trên đường thẳng d. Khi đó: M’ = Đ_d(M) $\iff \overrightarrow{M_{0}M\text{'}}=-\overrightarrow{M_{0}M}$

2) M’ = Đ_d(M) $\iff$M = Đ_d(M’).

II. Biểu thức tọa độ.

1) Chọn hệ trục tọa độ Oxy sao cho trục Ox trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’ ; y’) thì $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Ox. 

2) Chọn hệ trục tọa độ Oxy sao cho trục Oy trùng với đường thẳng d. Với mỗi điểm M = (x ; y), gọi M’ = Đ_d(M) = (x’; y’) thì $\left\{\begin{array}{c}x\text{'}=-x\\ y\text{'}=y\end{array}\right.$, đây là biểu thức tọa độ của phép đối xứng qua trục Oy.

Ví dụ 1. Cho điểm M(2 ; 4). Tìm ảnh của điểm M qua phép đối xứng qua trục Ox và trục Oy.

Lời giải:

Gọi Đ_Ox(M) = A(x ; y) và Đ_Oy(M) = B(a; b)

Áp dụng biểu thức tọa độ của phép đối xứng trục Ox ta có:

$$\begin{gathered} \left\{\begin{array}{c}x=2\\ y=-4\end{array}\right. \\ \Rightarrow A(2;-4) \end{gathered}$$

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta có:

$\left\{\begin{array}{c}a=-2\\ b=4\end{array}\Rightarrow B(-2;4)\right.$

III. Tính chất.

- Tính chất 1. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

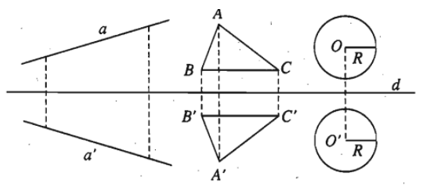
- Tính chất 2. Phép đối xứng trục biến đường thẳng thành đường thẳng, biến đoạn thẳng thành đoạn thẳng bằng nó, biến tam giác thành tam giác bằng nó, biến đường tròn thành đường tròn có cùng bán kính.

Ví dụ 2. Trong mặt phẳng tọa độ Oxy, qua phép đối xứng trục Ox, đường tròn (C)

(x – 2)² + (y – 3)² = 36 biến thành đường tròn (C’). Tìm phương trình đường tròn (C’) ?

Lời giải:

Đường tròn (C) có tâm I(2 ; 3) và bán kính là R = 6.

Qua phép đối xứng trục Ox, biến đường tròn (C) thành đường tròn (C’), biến tâm I thành tâm I’(x’; y’) và bán kính R’ = R = 6.

Áp dụng biểu thức phép đối xứng trục Ox ta được I’(2; – 3)

Do đó, phương trình đường tròn (C’) là:

(x – 2)² + (y + 3)² = 36.

IV. Trục đối xứng của một hình

- Định nghĩa. Đường thẳng d được gọi là trục đối xứng của hình ℋ nếu phép đối xứng qua đường thẳng d biến ℋ thành chính nó.

Khi đó, ta nói ℋ là hình có trục đối xứng.

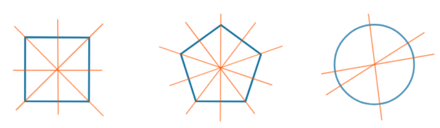
- Ví dụ 3. Các hình sau có trục đối xứng

Các dạng toán về phép đối xứng trục

Dạng 1. Xác định ảnh của một hình qua phép đối xứng trục.

Dạng 2. Tìm trục đối xứng của một hình.

Dạng 3. Tìm tập hợp điểm.

Dạng 4. Dùng phép đối xứng trục để dựng hình.

Bài tập tự luyện

1. Bài tập vận dụng

Bài 1. Mỗi hình sau có bao nhiêu trục đối xứng?

a) Hình gồm hai đường tròn có tâm và bán kính khác nhau.

b) Hình gồm hai đường thẳng d và d’ vuông góc với nhau.

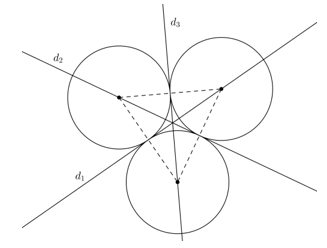
c) Hình gồm 3 đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau.

Lời giải:

Một đường tròn có vô số trục đối xứng đi qua tâm của đường tròn đó.

Do đó, trục đối xứng thỏa yêu cầu của bài toán là đường thẳng nối hai tâm của đường tròn đã cho.

Vậy hình gồm hai đường tròn có tâm và bán kính khác nhau có 1 trục đối xứng.

b) Có bốn trục đối xứng gồm đường thẳng d; d’ và hai đường phân giác của hai góc tạo bởi d, d’.

c) Có 3 trục đối xứng là 3 đường trung trực của các đoạn nối tâm.

Bài 2. Trong mặt phẳng Oxy, cho điểm M(2 ; 3). Tìm ảnh của M qua phép đối xứng qua đường thẳng d: x – y = 0?

Lời giải:

Gọi H là hình chiếu vuông góc của M trên d.

Ta có đường thẳng MH vuông góc với d nên đường thẳng MH có vectơ chỉ phương là:

$$\begin{gathered} \overrightarrow{u_{MH}}=\overrightarrow{n_d}=(1;-1) \\ \Rightarrow \overrightarrow{n_{MH}}=(1;1) \end{gathered}$$

Phương trình đường thẳng MH: 1.(x – 2) + 1.(y – 3) = 0 hay x + y – 5 = 0

Hai đường thẳng MH và d cắt nhau tại H nên tọa độ H là nghiệm hệ:

$\begin{array}{l}\left\{\begin{array}{c}x-y=0\\ x+y-5=0\end{array}\right.\\ \iff x=y=\frac{5}{2}\\ \Rightarrow H\left(\frac{5}{2};\frac{5}{2}\right)\end{array}$

Vì Đ_d(M) = M’ nên H là trung điểm của MM’.

$$\begin{gathered} \Rightarrow \left\{\begin{array}{c}{x}_{M\text{'}}=2x_H-x_M=3\\ y_{M\text{'}}=2y_H-y_M=2\end{array}\right. \\ \Rightarrow M\text{'}\left(3;2\right) \end{gathered}$$

Vậy M’(3; 2).

Bài 3. Trong mặt phẳng với hệ trục tọa độ Oxy, cho phép đối xứng trục Ox biến đường thẳng d: x + y – 2 = 0 thành đường thẳng d’. Viết phương trình d’.

Lời giải:

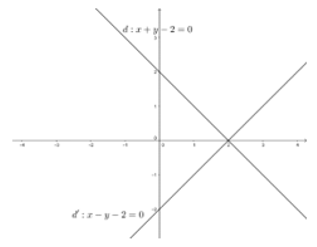
Lấy điểm M(x ; y) thuộc d suy ra:

x + y – 2 = 0  (1)

Gọi M’(x’; y’) là ảnh của M qua phép đối xứng trục Ox.

Khi đó ta có: $\left\{\begin{array}{c}x\text{'}=x\\ y\text{'}=-y\end{array}\right.$$\hspace{0.17em}\Rightarrow \left\{\begin{array}{c}x=x\text{'}\\ y=-y\text{'}\end{array}\right.$.  (2)

Thay (2) vào (1) ta được :

x’ – y’ – 2 = 0

Suy ra, phương trình đường thẳng d’ : x – y – 2 = 0.

Bài 4. Trong mặt phẳng tọa độ Oxy, cho đường thẳng đường tròn (C):

x² + y² – 2x – 4y – 4 =  0. Tìm ảnh của (C) qua phép đối xứng trục Oy.

Lời giải:

Đường tròn (C) có tâm I(1; 2) và bán kính $R=\sqrt{1^2+\text{\hspace{0.17em}\hspace{0.17em}}{2}^2-(-4)}=3$.

Gọi I’ và R’ là tâm và bán kính của (C’) là ảnh của đường tròn (C) qua phép đối xứng trục Oy.

Ta có: R’ = R = 3

Ta tìm tọa độ tâm I’.

Áp dụng biểu thức tọa độ của phép đối xứng trục Oy ta được I’(– 1; 2)

Phương trình đường tròn (C’): (x + 1)² + (y – 2)² = 9.

2. Bài tập tự luyện có đáp án