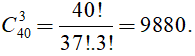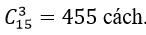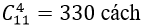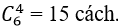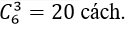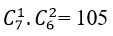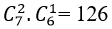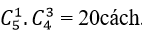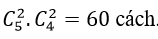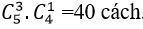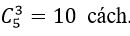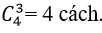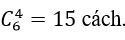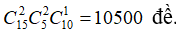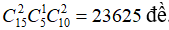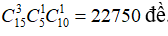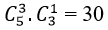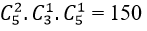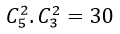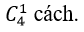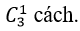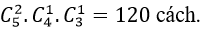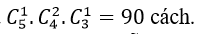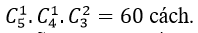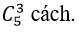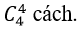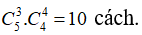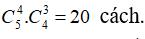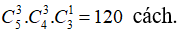250 Bài tập về Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án năm 2024) - Toán 11

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập Hoán vị - Chỉnh hợp - Tổ hợp Toán 11. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 11, giải bài tập Toán 11 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

Bài giảng Toán 11 Bài 2: Hoán vị - Chỉnh hợp - Tổ hợp

I. Kiến thức cần nhớ

Hoán vị

1. Định nghĩa

- Định nghĩa: Cho tập hợp A gồm n phần tử (n ≥ 1). Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp A được gọi là một hoán vị của n phần tử đó.

- Nhận xét: Hai hoán vị của n phần tử khác nhau ở thứ tự sắp xếp.

Chẳng hạn, hai hoán vị abc và cab của ba phần tử a; b; c là khác nhau.

2. Số các hoán vị

Kí hiệu: P_n là số các hoán vị của n phần tử.

- Định lí: P_n = n.(n – 1).(n – 2)….2.1

- Chú ý: Kí hiệu n.(n – 1)…2.1 là n! (đọc là n là giai thừa), ta có: P_n = n!.

- Ví dụ 1. Có bao nhiêu cách xếp 10 học sinh thành một hàng ngang.

Lời giải:

Số cách xếp 10 học sinh thành một hàng ngang là 10! cách.

Chỉnh hợp

1. Định nghĩa.

- Cho tập hợp A gồm n phần tử (n ≥ 1).

Kết quả của việc lấy k phần tử khác nhau từ n phần tử của tập hợp A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho.

- Ví dụ 2. Lớp 11A2 có 40 học sinh. Khi đó; mỗi cách chọn ra 4 bạn làm tổ trưởng tổ 1; tổ 2; tổ 3; tổ 4 chính là số chỉnh hợp chập 4 của 40 học sinh.

2. Số các chỉnh hợp

- Kí hiệu $A_{n}^{k}$ là số các chỉnh hợp chập k của n phần tử (1 ≤ k ≤ n) .

- Định lí:

$A_{n}^{k} = n (n - 1) ... (n - k + 1)$

- Ví dụ 3. Từ năm điểm phần biệt A; B; C; D; E ta lập được bao nhiêu vectơ khác $\vec{0}$ có điểm đầu và điểm cuối là năm điểm đã cho.

Lời giải:

Một vectơ được xác định khi biết điểm đầu và điểm cuối của nó.

Số vecto khác $\vec{0}$ có điểm đầu và điểm cuối là năm điểm đã cho chính là chỉnh hợp chập 2 của 5 phần tử:

Do đó, ta có: $A_{5}^{2} = 5.4.3 = 60$ vectơ thỏa mãn đầu bài.

- Chú ý:

a) Với quy ước 0! = 1 ta có: $A_{n}^{k} = \frac{n!}{(n - k)!}; 1 \leq k \leq n$ .

b) Mỗi hoán vị của n phần tử cũng chính là một chỉnh hợp chập n của n phần tử đó.

Vì vậy: $P_{n} = A_{n}^{n}$ .

Tổ hợp

1. Định nghĩa.

- Giả sử tập A có n phần tử (n ≥ 1). Mỗi tập con gồm k phần tử của A được gọi là một tổ hợp chập k của n phần tử đã cho.

- Chú ý: Số k trong định nghĩa cần thỏa mãn điều kiện 1 ≤ k ≤ n. Tuy vậy, tập hợp không có phần tử nào là tập rỗng nên ta quy ước gọi tổ hợp chập 0 của n phần tử là tập rỗng.

- Ví dụ 4. Cho tập A = {3; 4; 5; 6}.

Ta liệt kê các tổ hợp chập 3 của A là: {3; 4; 5}; {3; 4; 6}; {3; 5; 6}; {4; 5; 6}.

2. Số các tổ hợp.

Kí hiệu $C_{n}^{k}$ là số các tổ hợp chập k của n phần tử ( 0 ≤ k ≤ n).

- Định lí: $C_{n}^{k} = \frac{n!}{k! (n - k)!}$ .

Ví dụ 5. Cho 8 điểm phân biệt A; B; C; D; E; F; G; H, trong đó không có 3 điểm nào thẳng hàng, ta lập được bao nhiêu tam giác có 3 đỉnh là 8 điểm đã cho.

Lời giải:

Mỗi tam giác được lập là 1 tổ hợp chập 3 của 8 (điểm).

Vì vậy số tam giác có 3 đỉnh là 8 điểm đã cho là $C_{8}^{3} =$ 56.

3. Tính chất của các số $C_{n}^{k}$

a) Tính chất 1.

$C_{n}^{k} = C_{n}^{n - k}; 0 \leq k \leq n$

Ví dụ 7. $C_{8}^{4} + C_{8}^{5} = C_{9}^{5} = 126$ .

Các dạng bài toán về Hoán vị - Chỉnh hợp - Tổ hợp

Dạng 1. Bài toán chỉ sử dụng P hoặc C hoặc A.

Dạng 1.1 Chỉ sử dụng P.

Dạng 1.1.1 Bài toán đếm số.

Dạng 1.1.2 Bài toán chọn người (vật).

Dạng 1.2 Chỉ sử dụng C.

Dạng 1.2.1 Bài toán đếm số (tập số, tập hợp).

Dạng 1.2.2 Bài toán chọn người (vật).

Dạng 1.2.3 Bài toán liên quan đến hình học.

Dạng 1.3 Chỉ sử dụng A.

Dạng 1.3.1 Bài toán đếm số (tập số, tập hợp).

Dạng 1.3.2 Bài toán chọn người (vật).

Dạng 1.3.3 Bài toán liên quan đến hình học.

Dạng 2. Bài toán kết hợp hoán vị, tổ hợp, chỉnh hợp.

Dạng 2.1 Bài toán đếm số (tập số).

Dạng 2.2 Bài toán chọn người (vật).

Dạng 2.3 Bài toán liên quan đến hình học.

Dạng 3. Giải phương trình, bất phương trình, hệ liên quan đến hoán vị, chỉnh hợp, tổ hợp.

II. Bài tập tự luyện

Bài 1. Có 5 bạn nam và 5 bạn nữ. Hỏi có bao nhiêu cách xếp sao cho hai bạn cùng giới không đứng cạnh nhau.

Lời giải:

Đánh số 10 vị trí xếp từ 1 đến 10.

+ Trường hợp 1. Các bạn nam xếp ở vị trí lẻ, các bạn nữ xếp ở vị trí chẵn.

Xếp 5 bạn nam vào 5 vị trí lẻ có 5! = 120 cách

Xếp 5 bạn nữ vào 5 vị trí chẵn có 5! = 120 cách

Theo quy tắc nhân có: 120.120 = 14400 cách.

+ Trường hợp 2. Các bạn nam xếp ở vị trí chẵn, các bạn nữ xếp ở vị trí lẻ.

Tương tự trường hợp 1; có 14400 cách.

Vậy có tất cả: 14 400 + 14 400 = 28 800 cách.

Bài 2. Có 6 học sinh lớp 11 và 3 học sinh lớp 12 sẽ ngồi trên một hàng ngang có 9 ghế. Hỏi có bao nhiêu cách xếp chỗ ngồi cho 9 học sinh đó sao cho mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11?

Lời giải :

Do mỗi học sinh lớp 12 ngồi giữa hai học sinh khối 11 nên ở vị trí đầu tiên và cuối cùng của dãy ghế sẽ là học sinh khối 11.

Bước 1: Xếp 6 học sinh lớp 11 thành một hàng ngang, có 6! cách.

Bước 2: giữa 6 bạn học sinh lớp 11 có 5 khoảng trống, chọn 3 khoảng trống trong 5 khoảng trống để xếp các bạn lớp 12, có $A_{5}^{2}$ cách (có liên quan đến thứ tự).

Theo quy tắc nhân có $6! . A_{5}^{2} = 14400$ cách xếp thỏa yêu cầu.

Bài 3. Cho tập hợp A = {0; 1; 2; 3; 4; 5}. Có thể lập bao nhiêu số tự nhiên có 5 chữ số khác nhau?

Lời giải:

Xếp 5 phần tử của A vào 5 ô trống liền nhau, mỗi ô trống chỉ chứa 1 phần tử, không ô trống nào chứa cùng phần tử, số cách xếp ban đầu này là $A_{6}^{5} = 720$

Tương tự như vậy, nhưng mặc định ô trống đầu tiên là chứa phần tử 0, số cách xếp vào 4 ô trống còn lại tương ứng là $A_{5}^{4} = 120$ .

Số các số tự nhiên có 5 chữ số khác nhau được lập từ tập A là 720 – 120 = 600.

Bài 4. Cho hai đường thẳng song song a và b. Trên đường thẳng a có 7 điểm phân biệt, trên đường thẳng b có 6 điểm phân biệt. Hỏi có bao nhiêu tam giác có đỉnh là các điểm đã cho.

Lời giải:

+ Trường hợp 1: Tam giác được tạo thành có 2 đỉnh thuộc đường thẳng a và 1 đỉnh thuộc đường thẳng b.

Chọn 2 đỉnh thuộc a có $C_{7}^{2} = 21$ cách

Chọn 1 đỉnh thuộc b có 6 cách

Có 21.6 = 126 tam giác.

+ Trường hợp 2: Tam giác được tạo thành có 2 đỉnh thuộc đường thẳng b và 1 điểm thuộc đường thẳng a.

Chọn 2 đỉnh thuộc b có $C_{6}^{2} = 15$ cách

Chọn 1 đỉnh thuộc a có 7 cách

Có 15.7 = 105 tam giác.

Số các tam giác thỏa mãn đầu bài là: 126 + 105 = 231.

Bài 5: Một lớp học có 40 học sinh gồm 25 nam và 15 nữ. Chọn 3 học sinh để tham gia vệ sinh công cộng toàn trường, hỏi có bao nhiêu cách chọn như trên?

Lời giải:

Nhóm học sinh 3 người được chọn (không phân biệt nam, nữ - công việc) là một tổ hợp chập 3 của 40 (học sinh).

Vì vậy, số cách chọn nhóm học sinh là Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11

Bài 6: Trong mặt phẳng, cho 6 điểm phân biệt sao cho không có ba điểm nào thẳng hàng. Hỏi có thể lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập điểm đã cho?

Lời giải:

Cứ 3 điểm phân biệt không thẳng hàng tạo thành một tam giác.

Lấy 3 điểm bất kỳ trong 6 điểm phân biệt thì số tam giác cần tìm chính là một tổ hợp chập 3 của 6 phần tử (điểm).

Như vậy, ta có 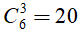Bài tập trắc nghiệm Đại số và Giải tích 11 | Bài tập và Câu hỏi trắc nghiệm Đại số và Giải tích 11 tam giác.

Bài 6: Có 15 tay đua xe đạp cùng xuất phát trong một cuộc đua để chọn ra 3 người về đích đầu tiên. Số kết quả có thể xảy ra là:

A.455 B.910 C.2730 D.2400

Lời giải:

Đáp án : A

Cần chọn ra 3 người về đích đầu tiên, nên giữa 3 người này không cần phải phân định thứ tự nhất nhì ba.

Số kết quả xảy ra là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Bài 7: Từ một nhóm gồm 6 nam và 5 nữ cần chọn ra 4 người trong đó có ít nhất một nữ. Hỏi có bao nhiêu cách chọn như vậy ?

A.75 B.330 C.315 D.325

Lời giải:

Đáp án : C

+ Số cách chọn ra 4 người bất kì từ 11 người là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

+ Số cách chọn ra 4 nam trong 6 nam là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

⇒ số cách chọn ra 4 người trong đó có ít nhất 1 nữ là: 330- 15= 315 cách

Bài 8: Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:

A.60 B.180 C.300 D.90

Lời giải:

Đáp án : A

Chọn 3 học sinh lớp 12 có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Chọn 1 học sinh lớp 11 có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Chọn 1 học sinh lớp 10 có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Do đó có; 4.3.5= 60 cách chọn

Bài 9: Hai đơn vị thi đấu cờ tướng A và B lần lượt có 5 người và 6 người. Cần chọn ra mỗi đơn vị 3 người để ghép cặp thi đấu với nhau. Hỏi có bao nhiêu cách thực hiện như thế?

A.1500 B.1600 C.1200 D.1540

Lời giải:

Đáp án : C

+ Số cách chọn 3 người từ đơn vị A là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

+ Số cách chọn 3 người từ đơn vị B là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

+ Sau khi chọn 3 người từ mỗi đơn vị; ta đi ghép các cặp đấu.

Đánh số thứ tự của 3 người từ đơn vị A lần lượt là 1; 2; 3.

Người thứ 1 của đơn vị B có 3 cách chọn; người thứ 2 của đơn vị B có 2 cách chọn và người thứ 3 của đơn vị B có 1 cách chọn.

⇒ Có 3.2.1= 6 cách ghép các cặp đấu.

Vậy có: 10 .20. 6= 1200 cách thực hiện việc ghép cặp thi đấu.

Bài 10: Cho 2 đường thẳng a và b song song với nhau.Trên đường thẳng a lấy 7 điểm phân biệt, trên đường thẳng b lấy 6 điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ 13 điểm đã cho?

A.240 B.231 C.210 D.180

Lời giải:

Đáp án : B

Số tam giác có 1 đỉnh nằm trên a và 2 đỉnh nằm trên b là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Số tam giác có 2 đỉnh nằm trên a và 1 đỉnh nằm trên b là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Do đó số tam giác có thể dựng được là : 105+ 126 = 231 tam giác

Bài 11: Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?

A.240 B.180 C.126 D.120

Lời giải:

Đáp án : D

Số cách chọn ban quản trị gồm 1 nam và 3 nữ là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Số cách chọn ban quản trị gồm 2 nam và 2 nữ là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Số cách chọn ban quản trị gồm 3 nam và 1 nữ là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Vậy tổng số cách chọn cần tìm là: 20+ 60+ 40= 120 cách.

Bài 12: Bạn Hồng có 15 bông hoa. Trong đó; có 5 bông hoa hồng; 4 bông hoa ly và 6 bông hoa lan. Hỏi bạn Hồng có bao nhiêu cách chọn ra 3 bông hoa hồng; 3 bông hoa ly và 4 bông hoa lan?

A.240 B.300 C.540 D.600

Lời giải:

Đáp án : D

+ Số cách chọn ra 3 bông hoa hồng từ 5 bông hoa hồng là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

+ Số cách chọn ra 3 bông hoa ly từ 4 bông hoa ly là : Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

+ Số cách chọn ra 4 bông hoa lan từ 6 bông hoa lan là: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

⇒ Số cách chọn thỏa mãn đầu bài là: 10 .4. 15= 600 cách.

Bài 13: Có 30 câu hỏi khác nhau gồm 5 câu khó, 10 câu trung bình, 15 câu dễ. Từ 30 câu đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu khác nhau, sao cho mỗi đề phải có 3loại câu hỏi (khó, trung bình, dễ) và số câu dễ không ít hơn 2?

A.56875 B.58765 C.87625 D.22575

Lời giải:

Đáp án : A

Trường hợp 1: Đề gồm 2 câu dễ, 2 câu khó, 1 câu trung bình thì có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 2: Đề gồm 2 câu dễ, 1 câu khó và 2 câu trung bình thì có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 3: Đề gồm 3 câu dễ, 1 câu khó và 1 câu trung bình thì có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Theo quy tắc cộng thì có 10500 + 23625 + 22750 = 56875 đề.

Bài 14: Một hộp bi có 5 viên bi đỏ, 5 viên bi vàng và 3viên bi xanh. Có bao nhiêu cách để lấy 4 viên bi từ hộp sao cho trong 4 viên bi lấy được số bi đỏ lớn hơn số bi vàng; biết rằng trong 4 viên bi lấy ra có bi màu xanh

A.180 B.150 C.210 D.270

Lời giải:

Đáp án : C

Trường hợp 1 : 4 bi lấy ra có: 3 đỏ; 1 xanh và 0 vàng: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 2 : 4 bi lấy ra có 2 đỏ; 1 xanh và 1 vàng: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 3 : 4 bi lấy ra có: 2 đỏ, 2 xanh và 0 vàng: Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

⇒ Số cách lấy thỏa mãn là: 30+ 150+ 30= 210 cách.

Bài 15: Đội thanh niên xung kích của một trường phổ thông có 12 học sinh, gồm 5 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp C. Cần chọn 4 học sinh đi làm nhiệm vụ sao cho 4 học sinh này thuộc không quá 2 trong 3 lớp trên. Hỏi có bao nhiêu cách chọn như vậy?

A.120 B.150 C.240 D.255

Lời giải:

Đáp án : D

Số cách chọn 4 học sinh bất kì từ 12 học sinh là 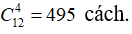Phương pháp giải bài tập Tổ hợp (cực hay có lời giải) cách.

Số cách chọn 4 học sinh mà mỗi lớp có ít nhất một em được tính như sau:

Trường hợp 1 : Lớp A có hai học sinh, các lớp B; C mỗi lớp có 1 học sinh:

Chọn 2 học sinh trong 5 học sinh lớp A có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Chọn 1 học sinh trong 4 học sinh lớp B có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Chọn 1 học sinh trong 3 học sinh lớp C có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Suy ra số cách chọn là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 2 : Lớp B có 2 học sinh, các lớp A, C mỗi lớp có 1 học sinh:

Tương tự ta có số cách chọn là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 3 : Lớp C có 2 học sinh, các lớp A, B mỗi lớp có 1 học sinh:

Tương tự ta có số cách chọn là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Vậy số cách chọn 4 học sinh mà mỗi lớp có ít nhất một học sinh là: 120 + 90 + 60 = 270 cách.

Số cách chọn ra 4 học sinh thuộc không quá 2 trong 3 lớp trên là: 495 – 270= 225 cách.

Bài 16: Từ 5 bông hồng vàng, 3 bông hồng trắng và 4 bông hồng đỏ (các bông hoa xem như đôi một khác nhau), người ta muốn chọn một bó hồng gồm 7 bông, hỏi có bao nhiêu cách chọn bó hoa trong đó có ít nhất 3 bông hồng vàng và 3 bông hồng đỏ?

A.200 cách B.210 cách C. 120 cách D. 150cách

Lời giải:

Đáp án : D

Ta thấy do chỉ chọn 7 bông hồng mà có ít nhất 3 bông hồng vàng và ít nhất 3 bông hồng đỏ nên chỉ có 3 trường hợp sau:

Trường hợp 1 : Chọn được 3 bông hồng vàng và 4 bông hồng đỏ.

Số cách chọn 3 bông hồng vàng là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Số cách chọn 4 bông hồng đỏ là Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Theo quy tắc nhân thì có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 2 : Chọn được 4 bông hồng vàng và 3 bông hồng đỏ.

Tương tự TH1 thì ta có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Trường hợp 3 : Chọn được 3 bông hồng vàng, 3 bông hồng đỏ và 1 bông hồng trắng.

Tương tự thì có Phương pháp giải bài tập Tổ hợp (cực hay có lời giải)

Vậy theo quy tắc cộng thì có: 10+ 20+ 120 = 150 cách.

Xem thêm các dạng bài tập liên quan khác:

250 Bài tập về Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án năm 2024)

100 Bài tập về Hoán vị – chỉnh hợp – tổ hợp (có đáp án năm 2024)

30 bài tập về Lý thuyết Số nguyên tố. Hợp số. Bảng số nguyên tố hay, chi tiết

Cách phân biệt hoán vị, chỉnh hợp, tổ hợp và bài tập (có đáp án) mới nhất 2024

Cách bấm chỉnh hợp, tổ hợp, xác suất trên máy tính cầm tay và bài tập vận dụng (2024) mới nhất

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Để xem toàn bộ tài liệu, vui lòng tải xuống

Được cập nhật 24/01/2024 1.6k lượt xem

Bởi Quynh Anh

Bình luận (0)

Đăng nhập để có thể bình luận

Chưa có bình luận nào. Bạn hãy là người đầu tiên cho tôi biết ý kiến!

Bài viết cùng chủ đề

Toán 11

120 Bài tập về cấp số nhân (có đáp án năm 2024) - Toán 11

1900.edu.vn xin giới thiệu Tổng hợp các dạng bài tập cấp số nhân Toán 11. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 11, giải bài tập Toán 11 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

388 7 tháng trước

Toán 11

70 Bài tập về một số phương trình lượng giác thường gặp (có đáp án năm 2024) - Toán 11

1900.edu.vn xin giới thiệu: Tổng hợp các dạng bài tập một số phương trình lượng giác thường gặp Toán 11. Đây sẽ là tài liệu tham khảo hữu ích, giúp các bạn học sinh ôn tập và củng cố kiến thức đã học, tự luyện tập nhằm học tốt môn Toán 11, giải bài tập Toán 11 tốt hơn. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây.

341 7 tháng trước

Toán 11

20 Bài tập về cách tìm tập xác định của hàm số lượng giác (2024) có đáp án

Bài viết 20 Bài tập về cách tìm tập xác định của hàm số lượng giác với phương pháp giải chi tiết giúp học sinh ôn tập, biết cách làm bài tập Cách tìm tập xác định của hàm số lượng giác.

828 8 tháng trước

250 Bài tập về Hoán vị - Chỉnh hợp - Tổ hợp (có đáp án năm 2024) - Toán 11

I. Kiến thức cần nhớ

II. Bài tập tự luyện

Để xem toàn bộ tài liệu, vui lòng tải xuống

Bình luận (0)

Bài viết cùng chủ đề

120 Bài tập về cấp số nhân (có đáp án năm 2024) - Toán 11

70 Bài tập về một số phương trình lượng giác thường gặp (có đáp án năm 2024) - Toán 11

20 Bài tập về cách tìm tập xác định của hàm số lượng giác (2024) có đáp án

Nội dung bài viết