50 Bài tập Rút gọn phân số (có đáp án năm 2024) - Toán lớp 5

Bài tập Rút gọn phân số

Kiến thức cần nhớ 

- Rút gọn phân số là cách làm đưa phân số đã cho thành phân số tối giản. Phân số mới vẫn bằng phân số đã cho.

- Phân số tối giản là phân số có tử số và mẫu số không chia hết cho số tự nhiên nào khác 1.

- Cách rút gọn phân số:

+ Xét xem cả tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

+ Chia cả tử số và mẫu số cho số đó.

+ Cứ làm như thế cho đến khi nhận được phân số tối giản.

Các dạng toán về rút gọn phân số

Dạng 1: Rút gọn rồi tìm các phân số bằng nhau

1. Phương pháp giải

- Đối với dạng toán này, chúng ta cần rút gọn phân số đã cho theo các bước trên rồi tiến hành so sánh các phân số tối giản. Nếu các phân số tối giản bằng nhau thì các phân số đã cho bằng nhau.

2. Ví dụ minh họa

Bài 1:

Trong các phân số dưới đây, phân số nào bằng $\frac{2}{3}$

Bài 2: Tìm các phân số bằng nhau trong các phân số sau

$\frac{5}{15}; \frac{1}{3}; \frac{12}{15}$

Rút gọn phân số: $\frac{5}{15}=\frac{5:5}{15:5}=\frac{1}{3}$

$\frac{12}{15}=\frac{12:3}{15:3}=\frac{4}{5}$          

Vậy các phân số bằng nhau là:$\frac{5}{15}=\frac{1}{3}$  

Dạng 2: Điền số thích hợp vào chỗ trống

1. Lý thuyết

- Dạng toán này người ta cho một phân số và yêu cầu chúng ta tìm tử số hoặc mẫu số của phân mới khi đã cho biết một mẫu số hoặc tử số.

2. Ví dụ minh họa

Bài 1: Điền số thích hợp vào chỗ trống: $\frac{1}{2}=\frac{\mathrm{...}}{18}$  

Hướng dẫn: Ta nhận thấy mẫu số của phân số mới là 18 lớn hơn mẫu số của phân số đã cho là 2. Vậy phân số cần tìm lớn hơn phân số đã cho. Nên ta lấy: 18 : 2 = 9. Sau đó ta lấy 9 nhân với tử số của mẫu số đã cho ta được số cần tìm: 9 x 1 = 9. Vậy số cần điền là: 9

Ta có thể trình bày như sau: $\frac{1}{2}=\frac{9}{18}$  

Bài 2: Điền số thích hợp vào chỗ trống: $\frac{9}{36}=\frac{3}{\mathrm{...}}$  

Hướng dẫn: Ta thấy tử số của phân số mới là 3 bé hơn tử số của phân số đã cho là 9. Vậy phân số cần tìm bé hơn phân số đã cho. Nên ta lấy 9 : 3 = 3. Sau đó ta lấy mẫu số của phân số đã cho chia cho 3, ta được số cần tìm là: 36 : 3 = 12.

Ta có thể trình bày như sau: $\frac{9}{36}=\frac{3}{12}$ 

Dạng 3: Rút gọn các thừa số giống nhau để tính nhanh

1. Lý thuyết

- Nếu tử số và mẫu số của phân số đều ở dưới dạng tích của nhiều thừa số, ta có thể rút gọn bằng cách gạch bỏ các thừa số giống nhau ở cả trên tử số và mẫu số. Sau khi gạch bỏ ta tính tích các thừa số còn lại.

- Nếu cả tử số và mẫu số của phân số đều ở dạng tích của nhiều thừa số, nhưng không có thừa số chung, ta có thể biến đổi các thừa số đó thành tích của các thừa số nhỏ hơn để rút gọn.

2. Ví dụ minh họa

Bài 1: Rút gọn phân số sau: $\frac{8x7x5}{11x8x7}$ 

Hướng dẫn: Ta nhận thấy cả tử số và mẫu số đều ở dưới dạng tích của nhiều thừa số. Tử số và mẫu số đều có chung thừa số là 7 và 8. Nên ta có thể gạch bỏ các thừa số chung này ở tử số và mẫu số.

Ta có thể trình bày như sau:

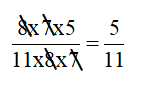
*Lưu ý: Dấu gạch chéo thể hiện là chúng ta đã rút gọn. Để  bài làm sạch sẽ, hs nên sử dụng bút chì để gạch.

Bài 2: Rút gọn phân số sau: $\frac{12x15x16}{4x8x24}$ 

Hướng dẫn: Chúng ta nhận thấy cả tử số và mẫu số đều ở dưới dạng tích của nhiều thừa số. Tuy nhiên lại không có thừa số chung. Ta có thể tách các thừa số thành tích của các số bé hơn. Sau đó rút gọn.

Ta có thể trình bày như sau:

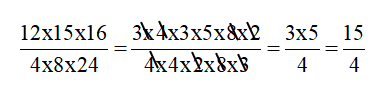
Bài tập tự luyện

1. Bài tập trắc nghiệm

Câu 1: Trong các phân số dưới đây, phân số nào là phân số tối giản

A.                 B.                      C.                       D.

Câu 2: Phân số tối giản là phân số:

A. Có tử số và mẫu số cùng chia hết cho số tự nhiên lớn hơn 1

B. Có tử số bằng 1 và mẫu số tùy ý

C. Có tử số và mẫu số không cùng chia hết cho số tự nhiên nào lớn hơn 1

D. Có tử số tùy ý và mẫu số bằng 1

Câu 3: Trong các phân số dưới đây, phân số nào là phân số tối giản

A.                    B.                        C.                              D.

Câu 4: Phân số sau khi rút gọn thành phân số tối giản là:

A.                     B.                          C.                             D.

Câu 5: Phân số sau khi rút gọn thành phân số tối giản là:

A.                      B.                         C.                            D.

2. Bài tập tự luận

Bài 1: Rút gọn các phân số dưới đây thành phân số tối giản

a, 

b, 

c, 

Bài 2: Tìm phân số tối giản trong các phân số sau: 

Bài 3: Tính theo mẫu: (cùng chia nhẩm tích ở trên và tích ở dưới gạch ngang lần lượt cho 2 rồi cho 5)

b, 

c, 

3. Hướng dẫn giải bài tập về rút gọn phân số

I. Bài tập trắc nghiệm

II. Bài tập tự luận

Bài 1: Các phân số tối giản cần tìm là: 

Bài 2:

a,

b,

c,

Bài 3:

b, 

c, 

Xem thêm các dạng bài tập liên quan khác:

50 Bài tập về Phân số bằng nhau.Rút gọn phân số (có đá án năm 2023)

50 Bài tập về Phép chia phân số (Có đáp án năm 2023)

60 Bài tập về Phép cộng phân số (có đáp án năm 2023)

60 Bài tập về Phép nhân phân số (có đáp án năm 2023)

60 Bài tập về Phép trừ phân số (có đáp án năm 2023)