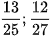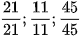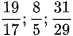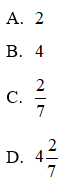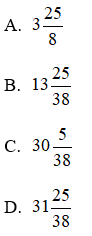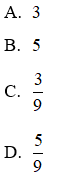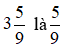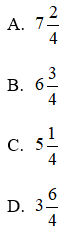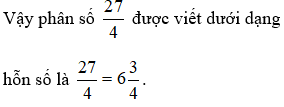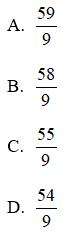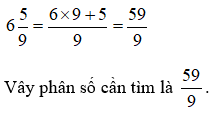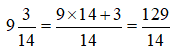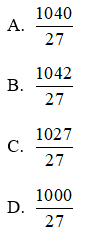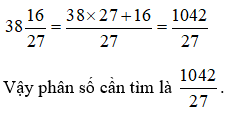Kiến thức cần nhớ
1. Khái niệm hỗn số
+ Khái niệm: Hỗn số gồm hai thành phần là phần nguyên và phần phân số.
Ví dụ: Cho hỗn số 3712
Phần nguyên của hỗn số là 3 và phần phân số là 712.
Nhận xét: Phần phân số của hỗn số bao giờ cũng bé hơn đơn vị.
+ Cách đọc hỗn số:
- Bước 1: đọc phần nguyên
- Bước 2: đọc “và”
- Bước 3: đọc phần phân số
Ví dụ: Hỗn số 3712 được đọc là “hai và một phần tư”.
2. Cách chuyển hỗn số thành phân số
+ Để chuyển một hỗn số thành phân số, ta thực hiện các bước sau:
- Bước 1: Lấy phần nguyên nhân với mẫu số, kết quả nhận được đem cộng với tử số
- Bước 2: Thay kết quả ở bước 1 thành tử số mới, giữ nguyên mẫu số. Ta được một phân số mới được chuyển từ hỗn số đã cho
Ví dụ: Chuyển các hỗn số thành phân số: 216;534;229
Lời giải:
216=2×6+16=136534=5×4+34=234229=2×9+29=209
3. Cách chuyển phân số thành hỗn số
+ Để chuyển một phân số sang hỗn số, ta thực hiện theo các bước sau:
- Bước 1: Lấy tử số chia cho mẫu số
- Bước 2: Phần nguyên là số nguyên trong hỗn số
- Bước 3: Phần dư là tử số mới trong hỗn số
- Bước 4: Phần mẫu số giữ nguyên giá trị
Ví dụ: Chuyển các phân số thành hỗn số: 92; 163; 275
Lời giải:
Ta có:
9 : 2 = 4 (dư 1); 16 : 3 = 5 (dư 1) và 27 : 5 = 5 (dư 2)
Vậy các phân số đã cho được viết dưới dạng hỗn số là:
92=412163=513275=525
* Chú ý: Bất kỳ phân số nào có tử số lớn hơn mẫu số đều có thể đổi thành hỗn số và ngược lại. Tuy nhiên nếu tử số bằng hoặc nhỏ hơn mẫu số thì không thể thực hiện được việc chuyển phân số thành hỗn số.
4. Phép tính hỗn số
+ Tương tự như với phân số, hỗn số có thể thực hiện các phép toán cộng, trừ, nhân, chia với nhau.
+ Để cộng hay trừ hỗn số, ta có hai cách làm sau:
- Cách 1: Chuyển hỗn số về dạng phân số rồi thực hiện các phép toán trên phân số
- Cách 2: Ta tách phần nguyên để thực hiện phép tính cộng trừ, tách phần phân số rồi thực hiện phép tính cộng trừ.
Ví dụ: Thực hiện phép tính sau bằng hai cách:
a) 156+213
b) 614−1112
Lời giải:
Cách 1:
a) 156+213=116+73
=116+146=256=416
b) 614−1112=254−1312
=7512−1312=6212=316=516
Cách 2:
a) 156+213
=(1+2)+(56+13)=3+(56+26)=3+76=3+116=416
b) 614−1112
=(6−1)+(14−112)=5+16=516
+ Để nhân hoặc chia hỗn số, ta chuyển hỗn số về dạng phân số rồi thực hiện các phép tính nhân chia trên phân số.
5. Phép cộng và phép trừ hỗn số
* Để thực hiện phép cộng và phép trừ hỗn số, ta có hai cách làm sau:
Cách 1: Chuyển hỗn số về phân số
+ Muốn cộng (hoặc trừ) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi cộng (hoặc) trừ hai phân số vừa chuyển đổi.
Ví dụ: Thực hiện phép tính:
a) 415+1615
b) 512−314
Lời giải:
a) 415+1615
=215+2115=6315+2115=8415
b) 512−314
=112−134=224−134=94
Cách 2: Tách hỗn số thành phần nguyên và phần phân số, sau đó thực hiện phép cộng (trừ) phần nguyên và phép cộng (trừ) phần phân số.
Ví dụ: Thực hiện phép tính:
a) 116+2712
b) 534−218
Lời giải:
a) 116+2712
=(1+2)+(16+712)=3+912=3+34=334
b) 534−218
=(5−2)+(34−18)=3+58=358
6. Phép nhân và phép chia hỗn số
+ Để thực hiện nhân (hoặc chia) hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi nhân (hoặc chia) hai phân số vừa chuyển đổi.
Ví dụ: Thực hiện phép tính:
a) 478×1313
b) 425:1715
Lời giải:
a) 478×1313
=398×1613=39×168×13=3×21×1=6
b) 425:1715
=225:2215=225×1522=3
7. So sánh hỗn số
* Để thực hiện so sánh hỗn số, ta có hai cách dưới đây:
Cách 1: Chuyển hỗn số về phân số: để so sánh hai hỗn số, ta chuyển hai hỗn số về dạng phân số rồi so sánh hai phân số vừa chuyển đổi.
Ví dụ: So sánh hai hỗn số: 514 và 223
Lời giải:
Ta có: 514=214 và 223=83
Quy đồng mẫu số hai phân số, ta có:
214=21×34×3=6312 83=8×43×4=3212
Vì 6312>3212 nên 514>223
Cách 2: So sánh phần nguyên và phần phân số. Khi so sánh hai hỗn số:
- Hỗn số nào có phần nguyên lớn hơn thì hỗn số đó lớn hơn và ngược lại hỗn số nào có phần nguyên nhỏ hơn thì hỗn số đó nhỏ hơn
- Nếu hai phần nguyên bằng nhau thì ta so sánh phần phân số, hỗn số nào có phần phân số lớn hơn thì hỗn số đó lớn hơn.
Ví dụ: So sánh các hỗn số sau:
a) 214 và 356
b) 4512 và 458
Lời giải:
a) 214 và 356
Hỗn số 214 có phần nguyên bằng 2 và hỗn số 356 có phần nguyên bằng 3
Vì 2 < 3 nên 214<356.
b) 4512 và 458
Hai hỗn số có cùng phần nguyên nên ta so sánh phần phân số của hai hỗn số
Vì 512<58 nên 4512<458
Bài tập tự luyện
Bài tập tự luyện số 1
Bài 1: Chuyển các phân số sau thành hỗn số rồi thực hiện phép tính:
a, d,
b, e,
c, f,
Bài 2: Tìm X, biết:
a,
b,
c,
Bài 3: Chuyển các phân số sau thành hỗn số (theo mẫu)
Mẫu: Có
= 2 (dư 3). Vậy
a, d,
b, e,
c,
Hướng dẫn giải
Bài 1:
Bài 2:
a, b,
c,
Bài 3:
Có = 2 (dư 1). Vậy
Có = 1 (dư 1). Vậy
Có = 5 (dư 2). Vậy
Có = 5 (dư 11). Vậy
Có = 15 (dư 2). Vậy
Bài 4:
a) Đọc các phân số sau:
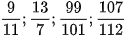
b) Viết các phân số sau:
– Năm phần mười ba
– Hai mươi bảy phần bốn mươi mốt
– Một trăm linh sáu phần một trăm bảy mươi chín.
Bài 5:
a) Viết thương các phép chia sau dưới dạng phân số
| 8 : 9 | 2 : 5 | 0 : 7 |
| 13 : 5 | 1 : 7 | 9 : 9 |
| 24 : 6 | 32 : 16 | 6 : 48 |
b) Cho các phân số sau:
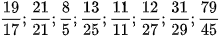
Hãy viết các phân số nhỏ hơn 1 bên trái, các phân số bằng 1 ở giữa và các phân số lớn hơn 1 bên tay phải. Giữa mỗi phần để một khoảng cách rộng hơn khoảng cách hai phân số thường để dễ phân biệt.
Bài 6:
a) Hãy so sánh mỗi cặp phân số sau bằng 2 cách:
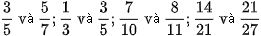
b) Hãy so sánh mỗi cặp phân số sau bằng 3 cách:

Bài 7:
Mẫu số của phân số có thể bằng 0 được không? Tại sao?
Bài 8:
a) Cho phân số 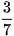 . Hãy tìm phân số bằng phân số đã cho nhưng có tử số là: 9 và 12.
. Hãy tìm phân số bằng phân số đã cho nhưng có tử số là: 9 và 12.
b) Cho phân số 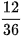 . Hãy tìm phân số bằng phân số đã cho nhưng có mẫu số bằng: 18; 9; 3.
. Hãy tìm phân số bằng phân số đã cho nhưng có mẫu số bằng: 18; 9; 3.
Hướng dẫn giải
Bài 4:
Phân số 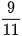 đọc là chín phần mười một.
đọc là chín phần mười một.
Còn lại, bạn đọc tự làm.
Phân số 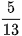 đọc là năm phần mười ba.
đọc là năm phần mười ba.
Còn lại, bạn đọc tự làm.
Bài 5:
a) 8 : 9 viết là 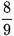 ; 24 : 6 viết là
; 24 : 6 viết là 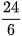
Còn lại, bạn đọc tự làm.
b)
|
Phân số nhỏ hơn 1 |
Phân số bằng hơn 1 |
Phân số lớn hơn 1 |
|
|
|
|
Bài 6:
a)
Cách 1: 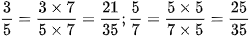
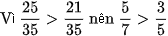
Cách 2: 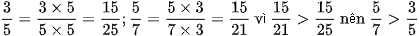
Còn lại, bạn đọc tự làm.
b)
Cách 1: 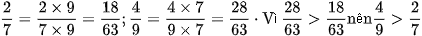
Cách 2: 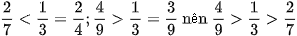
Còn lại, bạn đọc tự làm.
Bài 7:
Mẫu số của phân số là số chia trong phép chia. Số chia không thể bằng 0 nên mẫu số của phân số cũng không thể bằng 0.
Bài 8:
a) 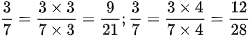
Vậy hai phân số phải tìm là: 
b) 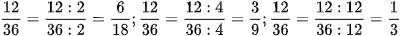
Vậy các phân số phải tìm là: 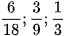
Bài tập tự luyện số 2
Bài 1:
Dựa vào hình vẽ để viết rồi đọc hỗn số thích hợp:
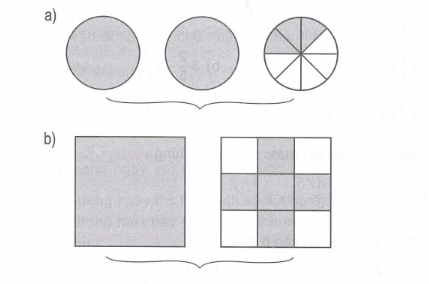
Bài 2:
Khoanh vào chữ đặt trước câu trả lời đúng:
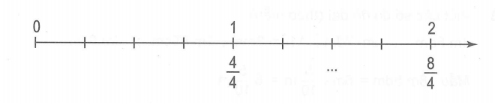
Hỗn số thích hợp để viết vào chỗ chấm dưới vạch của tia số trên là:
A.
B.
C.
D.
Bài 3:
Chuyển các hỗn số sau thành phân số:
Bài 4:
Đúng ghi Đ, sai ghi S:

Bài 5:
Tính:
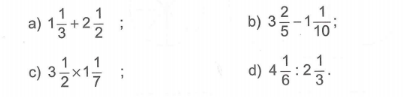
Bài 6:
Tìm X, biết:
a)
b)
c)
Bài 7:
Một bánh xe trung bình một giây quay được vòng. Hỏi trong
giây, bánh xe ấy quay được bao nhiêu vòng?
Bài 8: Một người đi xe đạp đi được km trong giờ đầu tiên. Giờ thứ hai người đó đi được
km. Vậy người đó phải đi quãng đường dài bao nhiêu ki-lô-mét nữa để đi hết đoạn đường, biết đoạn đường dài 16km.
Hướng dẫn giải
Bài 1:
a) Viết:
Đọc: hai và ba phần tám.
b) Viết:
Đọc: một và năm phần chín.
Bài 2:
Khoanh vào C.
Bài 3:
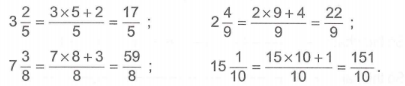
Bài 4:
a) S
b) Đ
c) Đ
d) S.
Bài 5:
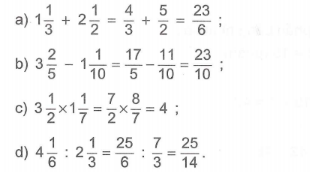
Bài 6:
a)
b)
c)
Bài 7:
Trong giây, bánh xe ấy quay được số vòng là:
(vòng)
Bài tập tự luyện số 3
Bài 1: Hỗn số gồm bao nhiêu thành phần?
A. Một thành phần, đó là phần nguyên
B. Một thành phần, đó là phần phân số
C. Hai thành phần, đó là phần nguyên và phần phân số.
Hướng dẫn giải
Hỗn số có hai thành phần là phần nguyên và phần phân số.
Bài 2: Chọn hỗn số trong các đáp án sau:
Hướng dẫn giải
Hỗn số có hai thành phần là phần nguyên và phần phân số. Vậy hỗn số là 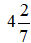
Bài 3: Chọn số thích hợp điền vào chỗ chấm:
Phần nguyên của hỗn số 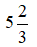
A. 5
B. 3
C. 4
D. 2
E. 1
Hướng dẫn giải
Phần nguyên của hỗn số 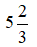
Vậy số thích hợp đặt vào ô trống là 5.
Bài 4: Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là:
Hướng dẫn giải
Hỗn số “mười ba và hai mươi lăm phần ba mươi tám” được viết là 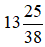
Bài 5: Phần phân số của hỗn số 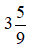
Hướng dẫn giải
Phần phân số của hỗn số
Bài 6: Phân số 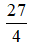
Hướng dẫn giải
Ta có: 27 : 4 = 6 dư 3.
Bài 7: Chuyển hỗn số 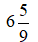
Hướng dẫn giải
Bài 8: Chuyển hỗn số 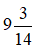
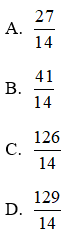
Hướng dẫn giải
Bài 9: Chuyển hỗn số 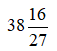
Hướng dẫn giải
Bài 10: Chọn số thích hợp đặt vào ô trống:
Khi chuyển phân số 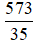
A. 17
B. 18
C. 16
D. 15
E. 14
Hướng dẫn giải
Bài tập tự luyện số 4
Bài 1: Chuyển các hỗn số thành phân số: 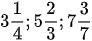 .
.
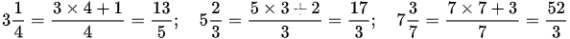
Bài 2: Chuyển các phân số thành hỗn số:  .
.
 dư 1;
dư 1;  dư 2
dư 2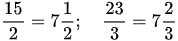
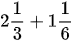
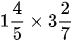

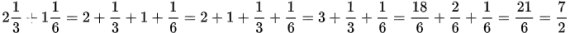
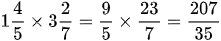
 và
và  .
. có phần nguyên là 3; hỗn số
có phần nguyên là 3; hỗn số  có phần nguyên là 1.
có phần nguyên là 1.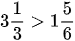 .
.Bài tập tự luyện số 5
Bài 1: Phần nguyên của hỗn số là:
A. 4
B. 2
C. 7
D. 9
Bài 2: Phần phân số của hỗn số là:
Bài 3: Phân số được chuyển thành hỗn số:
A.
B.
C.
D.
Bài 4: Kết quả của phép tính
A.
B.
C.
D.
Bài 5: Giá trị của thỏa mãn
là:
A. = 46
B. = 40
C. = 23
D. = 18
Bài 6: Tính rồi so sánh hai số A và B biết rằng:
và
A. A > B
B. A < B
C. A = B
Bài 7: Điền số thích hợp vào ô trống:
Một cửa hàng có kg gạo. Buổi sáng cửa hàng bán được
kg gạo. Buổi chiều cửa hàng bán được số gạo gấp 2 lần buổi sáng. Vậy sau cả hai buổi, cửa hàng còn lại ☐ ki-lô-gam gạo.
A. kg gạo
B. 38 kg gạo
C. kg gạo
D. kg gạo
Bài 8: Một hình chữ nhật có chiều dài m, chiều rộng kém chiều dài
m. Diện tích của hình chữ nhật đó là:
A. m2
B. m2
C. m2
D. m2
Bài 9: Một người đi xe đạp đi được km trong giờ đầu tiên. Giờ thứ hai người đó đi được
km. Vậy người đó phải đi quãng đường dài bao nhiêu ki-lô-mét nữa để đi hết đoạn đường, biết đoạn đường dài 16km.
A. km
B. km
C. km
D. km
Bài 10: Giá trị của biểu thức
A. 1
B. 2
C. 3
D. 4
Bài tập tự luyện số 6
I. TRẮC NGHIỆM
Khoanh tròn vào chữ cái trước câu trả lời đúng:
Câu 1: Phân số thích hợp chỉ phần tô đậm của hình sau là:
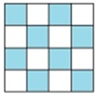
A. 32
B. 616
C. 12
D. 916
Câu 2: Viết thương 47:28 dưới dạng phân số ta được:
A. và
B.
C.
D.
Câu 3: Rút gọn phân số sau:
A.
B.
C. Không rút gọn được
D.
Câu 4: Trong các phân số sau, phân số nào là phân số thập phân:
A.
B.
C.
D.
Câu 5: Chuyển phân số sau thành phân số thập phân:
A.
B.
C.
D.
Câu 6: Hỗn số thích hợp biểu diễn số phần hình tròn được tô màu điền vào chỗ chấm là :
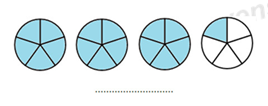
A.
B.
C.
D.
Câu 7: Tính:
A.
B.
C.
D.
Câu 8: Mẹ làm 20 chiếc bánh rán rất ngon, trong đó có số bánh rán là bánh ngọt, số bánh rán là bánh mặn, số bánh rán còn lại là bánh vừng. Hỏi mẹ đã làm bao nhiêu chiếc bánh vừng?
A. 7
B. 8
C. 6
D. 10
II. TỰ LUẬN
Câu 1. Tính:
Câu 2. Tính:
Câu 3: Phương, Hòa, Dương cùng hái dâu tây. Phương hái được 1 hộp và hộp, Hòa hái được 1 hộp và hộp, Dương hái được 1 hộp và hộp.
a) Viết hỗn số biểu diễn số hộp dâu tây mà mỗi bạn hái được:
b) Tính số hộp dâu tây cả ba bạn hái được:
c) Nếu đem tất cả số dâu tây hái được chia đều cho 3 bạn thì mỗi bạn được mấy phần hộp dâu tây?
Câu 4. Chuyển hỗn số thành phân số rồi thực hiện phép tính:
a)
b)
c)
d)
Câu 5. So sánh các hỗn số:
a)
b)
c)
d)
Xem thêm các dạng bài tập lớp 5 khác:
50 Bài tập Quy đồng mẫu số các phân số (có đáp án năm 2024)
50 Bài tập Giải toán về tỉ số phần trăm (có đáp án năm 2024)
50 Bài tập Tỉ số phần trăm (có đáp án năm 2024)
50 Bài tập Ôn tập: So sánh hai phân số (có đáp án năm 2024)
50 Bài tập Số thập phân, cách chuyển đổi và so sánh số thập phân (có đáp án năm 2024)