50 Bài tập Ôn tập: So sánh hai phân số (có đáp án năm 2024) - Toán lớp 5

Bài tập Ôn tập: So sánh hai phân số

Kiến thức cần nhớ 

1. So sánh hai phân số cùng mẫu số

Quy tắc: Trong hai phân số có cùng mẫu số:

+) Phân số nào có tử số bé hơn thì phân số đó bé hơn.

+) Phân số nào có tử số lớn hơn thì phân số đó lớn hơn.

+) Nếu tử số bằng nhau thì hai phân số đó bằng nhau.

Ví dụ:

$\frac{2}{5}<\frac{3}{5}, \frac{3}{5}>\frac{2}{5}, \frac{2}{5}=\frac{2}{5}$

2. So sánh hai phân số cùng tử số

Quy tắc: Trong hai phân số có cùng tử số:

+) Phân số nào có mẫu số bé hơn thì phân số đó lớn hơn.

+) Phân số nào có mẫu số lớn hơn thì phân số đó bé hơn.

+) Nếu mẫu số bằng nhau thì hai phân số đó bằng nhau.

Ví dụ:  

$\frac{1}{2}>\frac{1}{4}; \frac{2}{5}<\frac{2}{3}; \frac{5}{6}=\frac{5}{6}$

Chú ý: Phần so sánh các phân số cùng tử số, học sinh rất hay bị nhầm, các bạn học sinh nên chú ý nhớ và hiểu đúng quy tắc.

3. So sánh các phân số khác mẫu

a) Quy đồng mẫu số

Quy tắc: Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của hai phân số mới.

Phương pháp giải:

Bước 1: Quy đồng mẫu số hai phân số.

Bước 2: So sánh hai phân số có cùng mẫu số đó.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số $\frac{2}{3}$ và $\frac{3}{4}$.

Cách giải:

$\begin{array}{l}\frac{2}{3}=\frac{2\times 4}{3\times 4}=\frac{8}{12}\\ \frac{3}{4}=\frac{3\times 3}{4\times 3}=\frac{9}{12}\end{array}$

Ta có: $\frac{8}{12}<\frac{9}{12}$ (vì 8<9)

Vậy $\frac{2}{3}<\frac{3}{4}$.

b) Quy đồng tử số

Điều kiện áp dụng: Khi hai phân số có mẫu số khác nhau nhưng mẫu số rất lớn và tử số nhỏ thì ta nên áp dụng cách quy đồng tử số để việc tính toán trở nên dễ dàng hơn.

Quy tắc: Muốn so sánh hai phân số khác tử số, ta có thể quy đồng tử số hai phân số đó rồi so sánh các mẫu số của hai phân số mới.

Phương pháp giải:

Bước 1: Quy đồng tử số hai phân số.

Bước 2: So sánh hai phân số có cùng tử số đó.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số: $\frac{2}{125}$ và $\frac{3}{187}$

Cách giải:

Ta có: $\frac{2}{125}=\frac{2\times 3}{125\times 3}=\frac{6}{375}$

$\frac{3}{187}=\frac{3\times 2}{187\times 2}=\frac{6}{374}$

Vì 374<375 nên $\frac{6}{374}>\frac{6}{375}$.

Các dạng toán về ôn tập: so sánh hai phân số

Dạng 1: So sánh với 1

Điều kiện áp dụng:  Phương pháp này áp dụng cho dạng bài so sánh hai phân số, trong đó một phân số bé hơn 1 và một phân số lớn hơn 1.

Ví dụ: So sánh hai phân số $\frac{8}{9}$ và $\frac{7}{5}$.

Cách giải:

Vì $\frac{8}{9}<1$ và $1<\frac{7}{5}$ nên $\frac{8}{9}<\frac{7}{5}$

Dạng 2: So sánh với phân số trung gian

Điều kiện áp dụng: Phương pháp này áp dụng khi tử số của phân số thứ nhất bé hơn tử số của phân số thứ hai và mẫu số của phân số thứ nhất lại lớn hơn mẫu số của phân số thứ hai hoặc ngược lại. Khi đó ta so sánh với phân số trung gian là phân số có tử số bằng tử số của phân số thứ nhất, có mẫu số bằng mẫu số của phân số thứ hai hoặc ngược lại.

Phương pháp giải:

Bước 1: Chọn phân số trung gian.

Bước 2: So sánh hai phân số ban đầu với phân số trung gian.

Bước 3: Rút ra kết luận.

Lưu ý: So sánh hai phân số $\frac{a}{b}$ và $\frac{c}{d}$ (a, b, c, d  khác 0).

Nếu a > c và b < d (hoặc a < c và b>d  thì ta có thể chọn phân số trung gian là $\frac{a}{d}$ hoặc $\frac{c}{b}$

Ví dụ: So sánh hai phân số $\frac{27}{35}$ và $\frac{28}{33}$

Cách giải:

Chọn phân số trung gian là $\frac{27}{33}$

Ta thấy $\frac{27}{35}<\frac{27}{33} và \frac{27}{33}<\frac{28}{33} nên \frac{27}{35}<\frac{28}{33}$

Dạng 3: So sánh bằng phần bù 

Điều kiện áp dụng: Nhận thấy mẫu số lớn hơn tử số (phân số bé hơn 1) và hiệu của mẫu số với tử số của tất cả các phân số đều bằng nhau hoặc nhỏ thì ta tìm phần bù với 1.

Chú ý: Phần bù với 1 của phân số là hiệu giữa 1 và phân số đó.

Quy tắc: Trong hai phân số, phân số nào có phần bù lớn hơn thì phân số đó nhỏ hơn và ngược lại phân số nào có phần bù nhỏ hơn thì phân số đó lớn hơn.

Phương pháp giải:

Bước 1: Tìm phần bù của hai phân số.

Bước 2: So sánh hai phần bù với nhau.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số $\frac{997}{998}$ và $\frac{998}{999}$

Cách giải:

$\begin{array}{l}\frac{997}{998}=1-\frac{1}{998}\\ \frac{998}{999}=1-\frac{1}{999}\end{array}$

Vì 998<999 nên $\frac{1}{998}>\frac{1}{999}$. Do đó, $1-\frac{1}{998}<1-\frac{1}{999}$

Do đó, $\frac{997}{998}<\frac{998}{999}$.

Dạng 4: So sánh bằng phần hơn

Điều kiện áp dụng: Nhận thấy tử số lớn hơn mẫu số ( phân số lớn hơn 1) và hiệu của tử số với mẫu số của tất cả các phân số đều bằng nhau hoặc nhỏ thì ta tìm phần hơn với 1.

Chú ý: Phần hơn với 1 của phân số là hiệu giữa phân số đó và 1.

Quy tắc: Trong hai phân số, phân số nào có phần hơn lớn hơn thì phân số đó lớn hơn và ngược lại phân số nào có phần hơn nhỏ hơn thì phân số đó nhỏ hơn.

Phương pháp giải:

Bước 1: Tìm phần hơn của hai phân số.

Bước 2: So sánh hai phần hơn với nhau.

Bước 3: Rút ra kết luận.

Ví dụ: So sánh hai phân số $\frac{335}{333}$ và $\frac{279}{277}$

Giải

$\begin{array}{l}\frac{335}{333}=1+\frac{2}{333}\\ \frac{279}{277}=1+\frac{2}{277}\end{array}$

Vì 333>277 nên $\frac{2}{333}<\frac{2}{277}$. Do đó, $1+\frac{2}{333}<1+\frac{2}{277}$

Vậy $\frac{335}{333}<\frac{279}{277}$.

Bài tập tự luyện 

Bài tập tự luyện số 1

I. Bài tập trắc nghiệm

Câu 1: Trong các phân số dưới đây, phân số lớn hơn phân số  là:

A. $\frac{3}{5}$

B.

C.

D.

Câu 2: Trong các phân số dưới đây, phân số nhỏ hơn phân số là:

A.

B.

C.

D.

Câu 3: Dấu <, >, = thích hợp để điền vào chỗ chấm  là:

A. >

B. < 

C. = 

D. Không có dấu thích hợp

Câu 4: Phân số nào dưới đây bằng với số 1?

A.

B.

C.

D.

Câu 5: Phân số nào dưới đây bằng với phân số 

A.

B.

C.

D.

II. Bài tập tự luận

Bài 1: Điền dấu <, >, = thích hợp vào chỗ chấm:

$\frac{3}{4}...\frac{5}{6}$                              $\frac{1}{4}...\frac{5}{4}$

$\frac{6}{5}...\frac{6}{7}$                             $\frac{4}{15}...\frac{8}{30}$

Bài 2: Viết các phân số sau theo thứ tự từ bé đến lớn: 

Bài 3: Viết các phân số sau theo thứ tự từ lớn đến bé: 

Bài 4: So sánh các phân số sau với 1: 

Bài 5: Lan có một số quyển vở. Lan cho Hà số quyển vở và cho Hoa số quyển vở. Hỏi Lan cho bạn nào nhiều quyển vở hơn?

Hướng dẫn giải

I. Bài tập trắc nghiệm

Câu 1	Câu 2	Câu 3	Câu 4	Câu 5
D	A	B	C	D

II. Bài tập tự luận

Bài 1:

                                                                              

Bài 2: Vì  nên khi sắp xếp các phân số theo thứ tự từ bé đến hơn ta được 

Bài 3: Vì  nên khi sắp xếp các phân số theo thứ tự từ lớn đến bé ta được 

Bài 4: 

Bài 5:

Vì  nên . Vậy Lan cho Hoa nhiều quyển vở hơn

Bài tập tự luyện số 2

Câu 1: Dấu thích hợp để điền vào chỗ chấm  là:

Hướng dẫn giải

Câu 2: Dấu thích hợp để điền vào chỗ chấm  là:

Hướng dẫn giải

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của chúng.

Có 5 x 7 = 35 nên chọn 35 là mẫu số chung. Quy đồng mẫu số hai phân số, ta được:

Vì 28 > 15 nên  hay 

Câu 3:

Hướng dẫn giải

Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó rồi so sánh các tử số của chúng.

Vì 60 : 3 = 20; 60 : 15 = 4; 60 : 6 = 10; 60 : 12 = 5 nên chọn 60 là mẫu số chung. Quy đồng mẫu số các phân số, ta có:

Câu 4: Trong các phân số  có bao nhiêu phân số bé hơn phân số ?

Hướng dẫn giải

Câu 5: Phân số thích hợp để điền vào chỗ chấm  là:

Hướng dẫn giải

Bài tập tự luyện số 3

Bài 1: So sánh các cặp phân số sau:

a) $\frac{1}{3}$ và $\frac{-2}{3}$;

b) $\frac{5}{-4}$ và $\frac{7}{-4}$;

c) $\frac{-12}{13}$ và $\frac{10}{-13}$;

d) $\frac{5}{6}$ và $\frac{-7}{-6}$.

Bài 2: So sánh các cặp phân số sau:

a) $\frac{11}{12}$ và $\frac{13}{14}$;

b) $\frac{-7}{15}$ và $\frac{5}{-24}$;

c) $\frac{-4}{-25}$ và $\frac{1}{35}$.

Bài 3: So sánh các cặp phân số sau:

a) $\frac{20}{2000}$ và $\frac{30}{3000}$;

b) $\frac{-45}{75}$ và $\frac{27}{-90}$.

Bài 4: Sắp xếp các phân số sau theo thứ tự tăng dần: $\frac{-7}{4}$; $\frac{3}{4}$; $\frac{-1}{-4}$; $\frac{9}{-4}$.

Bài 5: Sắp xếp các phân số sau theo thứ tự giảm dần: $\frac{4}{9}$; $\frac{5}{-18}$; $-2$; $\frac{-7}{2}$; $\frac{-5}{-3}$.

Bài 6: Tìm số nguyên $x$ thỏa mãn:

a) $\frac{-4}{9}$ < $\frac{x}{9}$ < $\frac{2}{9}$;

b) $\frac{5}{-7}$ < $\frac{x}{-7}$ < $\frac{2}{-7}$.

Bài 7: Tìm số nguyên $x$ thỏa mãn:

a) $-1$ < $\frac{x}{12}$ < $\frac{-5}{6}$;

b) $\frac{7}{-3}$ > $\frac{2x}{3}$ > $-3$.

Bài 8: Tìm các số nguyên $x,y$ thỏa mãn:

$\frac{-1}{2}$ < $\frac{x}{-12}$ < $\frac{y}{3}$ < $\frac{1}{-4}$.

Bài 9: Tìm số nguyên $x$ thỏa mãn:

$\frac{-1}{4}$ > $\frac{x}{3}$ > $\frac{-1}{2}$.

Hướng dẫn giải

Bài 1:

a) $\frac{1}{3}$ và $\frac{-2}{3}$

Vì $1>-2$ nên $\frac{1}{3}$ > $\frac{-2}{3}$.

b) $\frac{5}{-4}$ và $\frac{7}{-4}$

+) Đưa về cùng mẫu dương:

$$\frac{5}{-4}=\frac{-5}{4};\frac{7}{-4}=\frac{-7}{4}$$

+) So sánh:

Vì $-5>-7$ nên $\frac{-5}{4}$ > $\frac{-7}{4}$.

Do đó:

$$\frac{5}{-4}>\frac{7}{-4}$$

c) $\frac{-12}{13}$ và $\frac{10}{-13}$

+) Đưa về cùng mẫu dương:

$$\frac{10}{-13}=\frac{-10}{13}$$

+) So sánh:

Vì $-12<-10$ nên $\frac{-12}{13}$ > $\frac{-10}{13}$.

Do đó:

$$\frac{-12}{13}<\frac{10}{-13}$$

d) $\frac{5}{6}$ và $\frac{-7}{-6}$

+) Đưa về cùng mẫu dương:

$$\frac{-7}{-6}=\frac{7}{6}$$

+) So sánh:

Vì 5 < 7 nên $\frac{5}{6}$ < $\frac{7}{6}$.

Do đó:

$$\frac{5}{6}<\frac{-7}{-6}$$

Bài 2:

a) $\frac{11}{12}$ và $\frac{13}{14}$

+) Quy đồng về cùng mẫu dương:

Mẫu chung là: BCNN(12, 14) = 84.

$$\frac{11}{12}=\frac{11\cdot 7}{12\cdot 7}=\frac{77}{84}$$

$$\frac{13}{14}=\frac{13\cdot 6}{14\cdot 6}=\frac{78}{84}$$

+) So sánh:

Ta có:

$$\frac{77}{84}<\frac{78}{84}$$

Do đó:

$$\frac{11}{12}<\frac{13}{14}$$

b) $\frac{-7}{15}$ và $\frac{5}{-24}$

+) Quy đồng về cùng mẫu dương:

Mẫu chung: BCNN(15, 24) = 120.

$$\frac{-7}{15}=\frac{(-7)\cdot 8}{15\cdot 8}=\frac{-56}{120}$$

$$\frac{5}{-24}=\frac{5\cdot (-5)}{(-24)\cdot (-5)}=\frac{-25}{120}$$

+) So sánh:

Ta có:

$$\frac{-56}{120}<\frac{-25}{120}$$

Do đó:

$$\frac{-7}{15}<\frac{5}{-24}$$

c) $\frac{-4}{-25}$ và $\frac{1}{35}$

+) Quy đồng về cùng mẫu dương:

Mẫu chung là: BCNN(25, 35) = 175.

$$\frac{-4}{-25}=\frac{(-4)\cdot (-7)}{(-25)\cdot (-7)}=\frac{28}{175}$$

$$\frac{1}{35}=\frac{1\cdot 5}{35\cdot 5}=\frac{5}{175}$$

+) So sánh:

Ta có:

$$\frac{28}{175}>\frac{5}{175}$$

Do đó:

$$\frac{-4}{-25}>\frac{1}{35}$$

Bài 3:

a) $\frac{20}{2000}$ và $\frac{30}{3000}$

Ta có:

$$\frac{20}{2000}=\frac{1}{100};\frac{30}{3000}=\frac{1}{100}$$

Vậy:

$$\frac{20}{2000}=\frac{30}{3000}$$

(vì cả hai phân số đều bằng $\frac{1}{100}$)

b) $\frac{-45}{75}$ và $\frac{27}{-90}$

+) Rút gọn:

$$\frac{-45}{75}=\frac{(-45):15}{75:15}=\frac{-3}{5}$$

$$\frac{27}{-90}=\frac{27:(-9)}{(-90):(-9)}=\frac{-3}{10}$$

+) Quy đồng về cùng mẫu dương:

Mẫu chung là: BCNN(5, 10) = 10.

$$\frac{-3}{5}=\frac{(-3)\cdot 2}{5\cdot 2}=\frac{-6}{10}$$

+) So sánh:

Ta có:

$$\frac{-6}{10}<\frac{-3}{10}$$

Do đó:

$$\frac{-3}{5}<\frac{-3}{10}$$

Suy ra:

$$\frac{-45}{75}<\frac{27}{-90}$$

Bài 4:

$\frac{9}{-4}$ < $\frac{-7}{4}$ < $\frac{-1}{-4}$ < $\frac{3}{4}$.

Bài 5:

Ta có:

$$\frac{4}{9}=\frac{8}{18}$$

$$\frac{5}{-18}=\frac{-5}{18}$$

$$-2=\frac{-36}{18}$$

$$\frac{-7}{2}=\frac{-63}{18}$$

$$\frac{-5}{-3}=\frac{30}{18}$$

Mà:

$\frac{30}{18}$ > $\frac{8}{18}$ > $\frac{-5}{18}$ > $\frac{-36}{18}$ > $\frac{-63}{18}$.

Do đó:

$\frac{-5}{-3}$ > $\frac{4}{9}$ > $\frac{5}{-18}$ > $-2$ > $\frac{-7}{2}$.

Bài 6:

a) $x$ là một trong các số -3; -2; -1; 0; 1.

b) Yêu cầu đề bài đồng nghĩa với: $\frac{-5}{7}$ < $\frac{-x}{7}$ < $\frac{-2}{7}$.

Suy ra: $-x=-4$ hoặc $-x=-3$.

Do đó: $x=4$ hoặc $x=3$.

Bài 7:

a) $-1$ < $\frac{x}{12}$ < $\frac{-5}{6}$

Yêu cầu trong đề bài tương đương với:

$\frac{-12}{12}$ < $\frac{x}{12}$ < $\frac{-10}{12}$.

Suy ra: $x=-11$.

b) $\frac{7}{-3}$ > $\frac{2x}{3}$ > $-3$

Yêu cầu trong đề bài tương đương với:

$\frac{-7}{3}$ > $\frac{2x}{3}$ > $\frac{-9}{3}$

Suy ra: $2x=-8$.

Do đó: $x=(-8):2=-4$.

Bài 8: Yêu cầu trong đề bài tương đương với:

$\frac{-6}{12}$ < $\frac{-x}{12}$ < $\frac{4y}{12}$ < $\frac{-3}{12}$.

Suy ra: $-x=-5$ và $4y=-4$.

Do đó: $x=5$ và $y=-1$.

Bài 9: Yêu cầu trong đề bài tương đương với:

$\frac{-3}{12}$ > $\frac{4x}{12}$ > $\frac{-6}{12}$.

Suy ra: $4x=-4$ hoặc $4x=-5$.

Tuy nhiên, $4x$ chia hết cho 2 nhưng -5 lại không chia hết cho 2, nên $4x=-5$ không thể xảy ra. Vậy ta chỉ có $4x=-4$. Do đó, $x=-4:4=-1$.

Bài tập tự luyện số 4

Bài 1: Điền số thích hợp vào chỗ chấm:

$\begin{array}{l}a.\frac{-11}{13}<\frac{...}{13}<\frac{...}{13}<\frac{...}{13}<\frac{-7}{13}\\ b.\frac{-1}{3}<\frac{...}{36}<\frac{...}{18}<\frac{-1}{4}\end{array}$

Hướng dẫn giải

a) Vì -11 < -10 < -9 < -8 < -7 nên $\frac{-11}{13}<\frac{-10}{13}<\frac{-9}{13}<\frac{-8}{13}<\frac{-7}{13}$

b) Quy đồng mẫu các phân số ta có:

$\frac{-12}{36}<\frac{-11}{36}<\frac{-10}{36}<\frac{-9}{36}$

Vì -12 < -11 < -10 < -9 nên ta có:

hay $\frac{-1}{3}<\frac{-11}{36}<\frac{-5}{18}<\frac{-1}{4}$

 Bài 2:

a) Thời gian nào dài hơn: $\frac{2}{3}$ h hay $\frac{3}{4}$ h?

b) Đoạn thẳng nào ngắn hơn: $\frac{7}{10}$m hay  $\frac{3}{4}$m ?

c) Khối lượng nào lớn hơn: $\frac{7}{8}$ kg hay $\frac{9}{10}$ ?

d) Vận tốc nào nhỏ hơn : $\frac{5}{6}$ km/h hay $\frac{7}{9}$ km/h ?

Hướng dẫn giải

Quy đồng mẫu.

a) Ta có: $\frac{2}{3}$.h = $\frac{8}{12}$.h và $\frac{3}{4}$.h = $\frac{9}{12}$.h, mà $\frac{9}{12}$ > $\frac{8}{12}$ nên $\frac{3}{4}$.h > $\frac{2}{3}$.h

b) Ta có: $\frac{7}{10}$.m=$\frac{14}{20}$.m và $\frac{3}{4}$.m = $\frac{15}{20}$.m, mà $\frac{14}{20}$ < $\frac{15}{20}$ nên $\frac{7}{10}$.m < $\frac{3}{4}$.m

c) Ta có: $\frac{7}{8}$.kg=$\frac{35}{40}$.kg và $\frac{9}{10}$.kg = $\frac{36}{40}$.kg, mà $\frac{35}{40}$ < $\frac{36}{40}$ nên $\frac{7}{8}$.kg < $\frac{9}{10}$.kg

d) Ta có: $\frac{5}{6}$.km/h = $\frac{15}{18}$.km/h và $\frac{7}{9}$.km/h = $\frac{14}{18}$.km/h, mà $\frac{15}{18}$ > $\frac{14}{18}$ nên $\frac{5}{6}$.km/h  > $\frac{15}{18}$

Đáp số:

a) $\frac{2}{3}$ h < $\frac{3}{4}$ hh ;

b) $\frac{7}{10}$m < $\frac{3}{4}$m

c) $\frac{7}{8}$ kg < $\frac{9}{10}$ kg

d) $\frac{5}{6}$ km/h > $\frac{7}{9}$ km/h 

Bài 3: Lớp 6B có  $\frac{4}{5}$ số học sinh thích bóng bàn, $\frac{7}{10}$ số học sinh thích bóng chuyền, $\frac{23}{25}$số học sinh thích bóng đá. Môn bóng nào được nhiều bạn học sinh lớp 6B yêu thích nhất ?

Hướng dẫn giải

Quy đồng mẫu các phân số đã cho.

Ta có  $\frac{4}{5}$ = $\frac{40}{50}$ , $\frac{7}{10}$ = $\frac{35}{50}$ , $\frac{23}{25}$ =$\frac{46}{50}$

Mà $\frac{35}{50}$ < $\frac{40}{50}$ < $\frac{46}{50}$

⇔  $\frac{7}{10}$<$\frac{4}{5}$<$\frac{23}{25}$ hay $\frac{23}{25}$ lớn nhất.

⇒ Môn bóng đá được yêu thích nhất 

Bài 4: Lưới nào sẫm nhất?

a) Đối với mỗi lưới ô vuông hình 7, hãy lập một phân số có tử số là ô đen, mẫu số là tổng số ô đen và ô trắng.

 

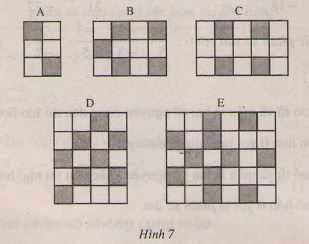
b) Sắp xếp các phân số này theo thứ tự tăng dần và cho biết lưới nào sẫm nhất (có tỉ số ô đen so với tổng số ô là lớn nhất.

Hướng dẫn giải

Lập các phân số rồi quy đồng mẫu các phân số vừa tìm được. Cũng có thể so sánh một số phân số đơn giản hơn với nhau rồi chọn phân số lớn nhất trong chúng để so sánh với những phân số còn lại.

a) Đối với mỗi lưới ô vuông ở hình vẽ, hãy lập một phân số có tử số là số ô xanh, mẫu là tổng số ô xanh và trắng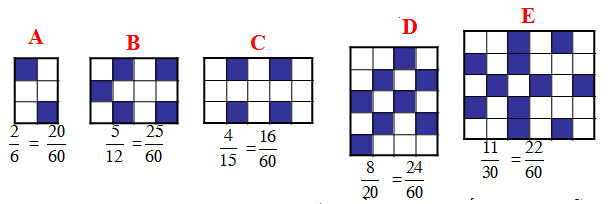

b) Sắp xếp các phân số theo thứ tự tăng dần và cho biết lưới nào sẫm nhất ?

$\frac{16}{60}<\frac{20}{60}<\frac{22}{60}<\frac{24}{60}<\frac{25}{60}=>\frac{4}{15}<\frac{2}{6}<\frac{11}{30}<\frac{8}{20}<\frac{5}{12}$

Vậy: Lưới sẫm nhất là lưới B

Bài 5: Đối với phân số ta có tính chất : Nếu $\frac{\mathrm{a}}{\mathrm{b}}$ > $\frac{\mathrm{c}}{\mathrm{d}}$và $\frac{\mathrm{c}}{\mathrm{d}}$ > $\frac{\mathrm{p}}{\mathrm{q}}$  thì  $\frac{\mathrm{a}}{\mathrm{b}}$ > $\frac{\mathrm{p}}{\mathrm{q}}$.

Dựa vào tính chất này, hãy so sánh:

a) $\frac{6}{7}$ và $\frac{11}{10}$

b) -$\frac{5}{17}$ và $\frac{2}{7}$

c) $\frac{419}{-723}$ và $\frac{-697}{-313}$

Hướng dẫn giải

$\begin{array}{l}a.\frac{6}{7}<1<\frac{11}{10}=>\frac{6}{7}<\frac{11}{10}\\ b.\frac{-5}{17}<0<\frac{2}{7}=>\frac{-5}{17}<\frac{2}{7}\\ c.\frac{419}{-723}=\frac{-419}{723}<0<\frac{-697}{-313}=\frac{697}{313}=>\frac{419}{-723}<\frac{-697}{-313}\end{array}$

Bài 6:

Thời gian nào dài hơn: $\frac{1}{2}$ giờ hay $\frac{4}{5}$?

Đoạn thẳng nào ngắn hơn: $\frac{2}{3}$ mét hay $\frac{3}{5}$ mét?

Khối lượng nào lớn hơn: $\frac{6}{7}$ kilogam hay $\frac{7}{8}$ kilogam?

Hướng dẫn giải

a. Ta có: $\frac{1}{2}$ giờ = $\frac{5}{10}$ giờ; $\frac{4}{5}$ giờ = $\frac{8}{10}$ giờ

Vì $\frac{5}{8}$ <$\frac{8}{10}$ nên $\frac{1}{2}$ giờ < $\frac{4}{5}$ giờ

Vậy thời gian $\frac{4}{5}$ giờ dài hơn

b. Ta có: $\frac{2}{3}$ mét = $\frac{10}{15}$ mét ; $\frac{3}{5}$ mét = $\frac{9}{15}$ mét

Vì $\frac{10}{15}$ > $\frac{9}{15}$ nên $\frac{2}{3}$ mét > $\frac{3}{5}$ mét

Vậy đoạn thẳng $\frac{3}{5}$ mét ngắn hơn

c. Ta có: $\frac{6}{7}$ kilogam = $\frac{48}{56}$ kilogam; $\frac{7}{8}$ kilogam = $\frac{49}{56}$ kilogam

Vì $\frac{48}{56}$ < $\frac{49}{56}$ nên $\frac{6}{7}$ kg < $\frac{7}{8}$ kg

Vậy khối lượng $\frac{7}{8}$ kilogam lớn hơn

Bài 7: Điền số thích hợp vào chỗ trống:

$\begin{array}{rl}& a.\frac{-12}{17}<\frac{...}{17}<\frac{...}{17}<\frac{...}{17}<\frac{-8}{17}\\ & b.\frac{-1}{2}<\frac{...}{24}<\frac{...}{12}<\frac{...}{8}<\frac{-1}{3}\end{array}$

Hướng dẫn giải

Dựa vào quy tắc so sánh hai phân số cùng mẫu ta có:

$\frac{-12}{17}<\frac{-11}{17}<\frac{-10}{17}<\frac{-9}{17}<\frac{-8}{17}$

Dựa vào quy tắc so sánh hai phân số không cùng mẫu ta có:

$\frac{-1}{2}<\frac{...}{24}<\frac{.2}{12.2}<\frac{.3}{8.3}<\frac{-1.8}{3.8}$

=>$\frac{-12}{24}<\frac{-11}{24}<\frac{-10}{12.2}<\frac{-9}{8.3}<\frac{-8}{3.8}$

Vậy $\frac{-1}{2}<\frac{-11}{24}<\frac{-5}{12}<\frac{-3}{8}<\frac{-1}{3}$

Bài 8: So sánh các phân số

$\begin{array}{rl}& a.\frac{5}{24};\frac{5+10}{24};\frac{5}{8}\\ & b.\frac{4}{9};\frac{6+9}{6.9};\frac{2}{3}\end{array}$

Hướng dẫn giải

a. Ta có: $\frac{5+10}{24}=\frac{15}{24}=\frac{5}{8}$

Vậy $\frac{5}{24}>\frac{5+10}{24}=\frac{5}{8}$

b. Ta có: $\frac{6+9}{6.9}=\frac{15}{54}=\frac{5}{18}$

Mà $\frac{4}{9}=\frac{8}{18};\frac{5}{18}=\frac{5}{18};\frac{2}{3}=\frac{12}{18}$

Vì $\frac{5}{18}<\frac{8}{18}<\frac{12}{18}$ nên $\frac{6+9}{6.9}<\frac{4}{9}<\frac{2}{3}$

Bài tập tự luyện số 5

I. TRẮC NGHIỆM

Câu 1: Đáp án đúng trong các đáp án sau là:

A. $\frac{5}{13}>\frac{4}{13}$

B. $\frac{1}{2}<\frac{2}{4}$

C. $\frac{8}{9}>\frac{9}{8}$

D. $\frac{2}{3}>1$

Câu 2: Chọn đáp án sai trong các đáp án sau:

A. $\frac{1}{5}<\frac{1}{2}$

B. $\frac{7}{4}<\frac{16}{13}$

C. $\frac{8}{5}>\frac{3}{4}$

D. $\frac{5}{6}<\frac{7}{8}$

Câu 3: Các phân số $\frac{3}{10},\frac{4}{15},\frac{1}{3}$ được sắp xếp theo thứ tự từ bé đến lớn là:

A. $\frac{3}{10},\frac{4}{15},\frac{1}{3}$

B. $\frac{1}{3},\frac{3}{10},\frac{4}{15}$

C. $\frac{4}{15},\frac{1}{3},\frac{3}{10}$

D. $\frac{4}{15},\frac{3}{10},\frac{1}{3}$

Câu 4: Các dấu $>,<,=$được điền vào trong các chỗ chấm sau theo thứ tự đúng là:

$\frac{5}{9}\mathrm{....1};\frac{4}{3}\mathrm{.....1};\mathrm{1....}\frac{9}{8};\frac{7}{7}\mathrm{....1}$

A. $<;<;>;=$

B. $>;<;<;=$

C. $<;>;<;=$

D. $>;<;=;=$

Câu 5: So sánh hai phân số $\frac{5}{6}$và $\frac{3}{8}$ta được:

A. $\frac{5}{6}<\frac{3}{8}$

B. $\frac{5}{6}>\frac{3}{8}$

C. $\frac{5}{6}=\frac{3}{8}$

D. Không so sánh được.

Câu 6: Phân số lớn nhất trong các phân số $\frac{14}{15};\frac{15}{16};\frac{16}{17};\frac{17}{18}$là:

A. $\frac{14}{15}$

B. $\frac{15}{16}$

C. $\frac{16}{17}$

D. $\frac{17}{18}$

Câu 7: Phân số bé nhất trong các phân số $\frac{3}{4};\frac{2}{7};\frac{5}{6};\frac{19}{17}$ là:

A. $\frac{3}{4}$

B. $\frac{2}{7}$

C. $\frac{5}{6}$

D. $\frac{19}{17}$

Câu 8: Sắp xếp dãy các phân số  theo thứ tự giảm dần ta được:

A. $\frac{4}{5};\frac{3}{7};\frac{5}{8}$

B. $\frac{3}{7};\frac{5}{8};\frac{4}{5}$

C. $\frac{4}{5};\frac{3}{7};\frac{5}{8}$

D. $\frac{4}{5};\frac{5}{8};\frac{3}{7}$

II. TỰ LUẬN:

Câu 1: Điền dấu $>,<,=$ vào ô trống

$$\begin{gathered} \frac{3}{7} \square \frac{5}{7} \\ \frac{2}{4} \square \frac{6}{12} \\ \frac{8}{4} \square \frac{4}{7} \\ \frac{14}{25} \square \frac{14}{17} \\ \frac{2}{3} \square \frac{4}{5} \\ \frac{7}{8} \square \frac{9}{11} \end{gathered}$$

Câu 2: Điền dấu $>,<,=$ vào ô trống

$$\begin{gathered} \frac{3}{4}+\frac{25}{100} \square \frac{75}{100}+\frac{1}{4} \\ 3+\frac{15}{19} \square 2+\frac{15}{19} \\ 3+\frac{14}{19} \square 3+\frac{19}{14} \\ 3+\frac{15}{19} \square 4-\frac{4}{19} \end{gathered}$$

Câu 3: Không quy đồng mẫu số, hãy so sánh các phân số sau:

$$\begin{gathered} \frac{1995}{1996} \square \frac{1996}{1997} \\ \frac{2121}{3737} \square \frac{212121}{373737} \\ \frac{18}{17} \square \frac{13}{27} \\ \frac{16}{27} \square \frac{15}{29} \\ \frac{2010}{2011} \square \frac{17}{16} \\ \frac{327}{326} \square \frac{326}{325} \end{gathered}$$

Câu 4: Viết các phân số : $\frac{12}{17};\frac{19}{15};\frac{19}{13};\frac{15}{17};\frac{12}{12}$ theo thứ tự giảm dần.

Bài tập tự luyện số 6

Bài 1: Các học sinh của lớp 6B yêu thích nhiều môn thể thao. Trong đó, $\frac{1}{2}$ số học sinh của lớp thích môn bóng đá; $\frac{2}{5}$ số học sinh thích môn bóng chuyền; $\frac{11}{20}$ số học sinh thích môn bóng rổ; và $\frac{3}{10}$ số học sinh thích môn cầu lông. Em hãy cho biết môn thể thao nào được các học sinh lớp 6B yêu thích nhất?

Bài 2: Bạn Việt là một người rất thích đi xe đạp vào cuối tuần. Ngày thứ Bảy, bạn đi được 31 km trong 2 giờ. Ngày chủ nhật, bạn đi được 46 km trong 3 giờ. Hỏi ngày nào bạn Việt đạp xe nhanh hơn?

Bài 3: Một cửa hàng có bán ba loại mì gói với khối lượng và giá tiền mỗi gói như sau:

Tên mì	HẢO HẢO	CUNG ĐÌNH	OMACHI
Khối lượng (g)	$67$	$80$	$68$
Giá tiền (đ)	$8600$	$7000$	$10500$

Em hãy cho biết loại mì nào rẻ nhất, loại mì nào đắt (mắc) nhất?

Bài 4: Tại một cửa hàng kia, sản phẩm nước ngọt có giá 13 nghìn đồng mỗi chai. Vào tuần lễ cuối tháng, sản phẩm này được khuyến mãi dưới hai hình thức:

• Hình thức 1: Giảm giá 2 nghìn đồng mỗi chai;
• Hình thức 2: Mua 2 tặng 1.

Theo em, mua hàng theo hình thức nào thì có lợi hơn về giá.

Xem thêm các dạng bài tập liên quan khác:

50 Bài tập về Phân số bằng nhau.Rút gọn phân số (có đá án năm 2023)

50 Bài tập về Phép chia phân số (Có đáp án năm 2023)

60 Bài tập về Phép cộng phân số (có đáp án năm 2023)

60 Bài tập về Phép nhân phân số (có đáp án năm 2023)

60 Bài tập về Phép trừ phân số (có đáp án năm 2023)