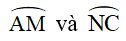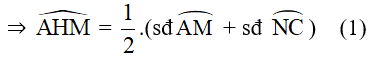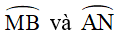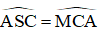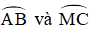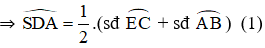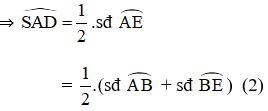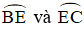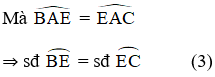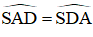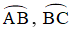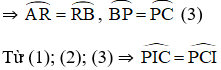50 Bài tập Góc có đỉnh ở bên trong đường tròn. Góc có đỉnh ở bên ngoài đường tròn (có đáp án năm 2024) - Toán 9

Góc có đỉnh ở bên trong đường tròn

Góc có đỉnh ở bên ngoài đường tròn

Kiến thức cần nhớ 

1. Góc có đỉnh ở bên trong đường tròn

- Góc có đỉnh nằm bên trong đường tròn được gọi là góc có đỉnh ở bên trong đường tròn.

- Định lí: Số đo của góc có đỉnh ở bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.

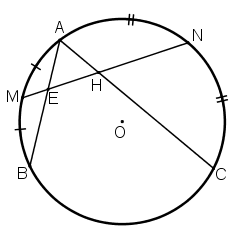
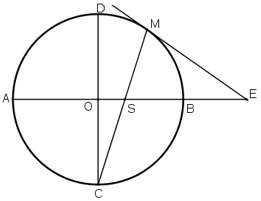
Ví dụ 1. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên trong đường tròn) như hình vẽ.

Trong hình vẽ trên, $\widehat{BEC}$ là góc có đỉnh nằm ở bên trong đường tròn chắn hai cung là .

Do đó,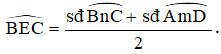 

2. Góc có đỉnh nằm bên ngoài đường tròn

- Góc có đỉnh ở bên ngoài đường tròn là góc có đỉnh nằm ngoài đường tròn và các cạnh đều có điểm chung với đường tròn.

- Định lí: Số đo của góc có đỉnh ở bên ngoài đường tròn bằng nửa hiệu số đo hai cung bị chắn.

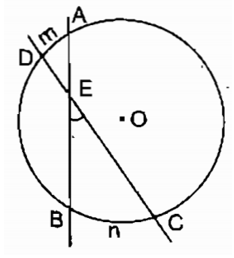
Ví dụ 2. Cho đường tròn (O) có hai dây AB và CD cắt nhau tại E (điểm E nằm bên ngoài đường tròn) như hình vẽ.

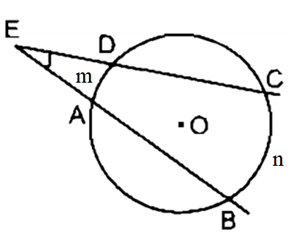
Trong hình vẽ trên, $\widehat{BEC}$ là góc có đỉnh nằm ở bên ngoài đường tròn chắn hai cung là $\stackrel{⏜}{BnC},\stackrel{⏜}{AmD}$.

Do đó,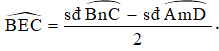 

Bài tập tự luyện (có hướng dẫn)

Bài 1: Cho đường tròn (O) và hai dây AB, AC. Gọi M, N lần lượt là điểm chính giữa của cung AB và cung AC. Đường thẳng MN cắt dây AB tại E và cắt dây AC tại H. Chứng minh tam giác AEH là tam giác cân.

Lời giải

+ Do góc 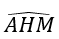 là góc có đỉnh bên trong đường tròn chắn hai cung 

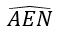
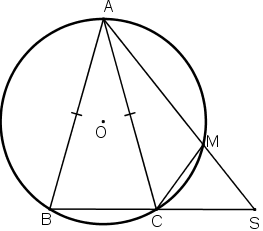
+ Do góc  là góc có đỉnh bên trong đường tròn chắn hai cung 

Bài 2: Cho đường tròn (O) và hai dây AB, AC bằng nhau. Trên cung nhỏ AC lấy một điểm M. Gọi S là giao điểm của AM và BC.

Lời giải

+ Đường tròn (O) có dây AB = AC

+  là góc có đỉnh ngoài đường tròn chắn hai cung 

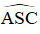
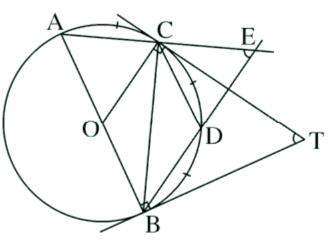
Bài 3: Trên một đường tròn, lấy liên tiếp ba cung AC,CD, DB sao cho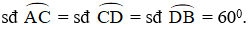 Hai đường thẳng AC và DB cắt nhau tại E. Hai tiếp tuyến của đường tròn tại B và C cắt nhau tại T. Chứng minh rằng:

Lời giải

a)

Ta có: AB là đường kính của (O)

$\Rightarrow$ sđ $\stackrel{⏜}{AB}={180}^o$

$\Rightarrow$ sđ $\stackrel{⏜}{BAC}=$sđ $\stackrel{⏜}{AB}$ + sđ $\stackrel{⏜}{AC}={180}^o+{60}^o={240}^o$

Mặt khác ta có: sđ $\stackrel{⏜}{BDC}$ = sđ $\stackrel{⏜}{CD}$ + sđ $\stackrel{⏜}{DB}$$={60}^o+{60}^o={120}^o$ 

Góc BTC là góc có đỉnh nằm bên ngoài đường tròn (O) nên ta có:

$\widehat{BTC}=\frac{1}{2}$(sđ $\stackrel{⏜}{BAC}$ - sđ $\stackrel{⏜}{BDC}$) $=\frac{1}{2}\left({240}^o-{120}^o\right)={60}^o$ (1)

Góc AEB là góc có đỉnh nằm bên ngoài đường tròn (O) nên ta có:

$\widehat{AEB}=\frac{1}{2}$(sđ $\stackrel{⏜}{AB}$ - sđ $\stackrel{⏜}{CD}$) $=\frac{1}{2}\left({180}^o-{60}^o\right)={60}^o$ (2)

Từ (1) và (2) ta suy ra: $\widehat{BTC}=\widehat{AEB}$ (đcpcm)

b)

Góc DCT là góc tạo bởi tiếp tuyến CT và dây cung CD của (O) $\Rightarrow \widehat{DCT}=\frac{1}{2}$sđ $\stackrel{⏜}{CD}$. Lại có: Góc BCD là góc nội tiếp chắn cung BD của (O) $\Rightarrow \widehat{BCD}=\frac{1}{2}$ sđ $\stackrel{⏜}{BD}$

Mà sđ $\stackrel{⏜}{CD}$ = sđ $\stackrel{⏜}{BD}$ (gt)

$\Rightarrow \widehat{DCT}=\widehat{BCD}$

Mà tia CD nằm giữa hai tia CB và CT.

Do đó, CD là tia phân giác của góc BCT .

Bài 4: Cho AB và CD là hai đường kính vuông góc của đường tròn (O). Trên cung nhỏ BD lây một điểm M . Tiếp tuyến tại M cắt tia AB ở E, đoạn thẳng CM cắt AB ở S.Chứng minh ES = EM.

Lời giải

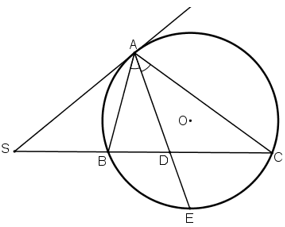
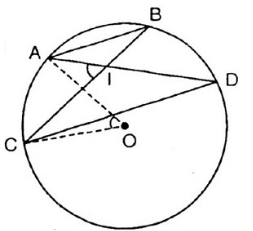
Bài 5: Qua điểm S nằm bên ngoài đường tròn (O), vẽ tiếp tuyến SA và cát tuyến SBC của đường tròn. Tia phân giác của góc BAC cắt dây BC tại D. Chứng minh SA = SD.

Lời giải

Tia phân giác AD cắt (O) tại E.

+  là góc có đỉnh nằm bên trong đường tròn

+  là góc tạo bởi tiếp tuyến AS và dây AE

+  lần lượt là các góc nội tiếp chắn các cung 

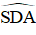
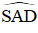
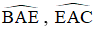
Từ (1); (2) và (3) suy ra 

⇒ ΔSAD cân tại S

⇒ SA = SD.

Bài 6: Qua điểm A nằm bên ngoài đường tròn (O) vẽ hai cát tuyến ABC và AMN sao cho hai đường thẳng BN và CM cắt nhau tại một điểm S nằm bên trong đường tròn.

Chứng minh $\widehat{A}+\widehat{BSM}=2\widehat{CMN}$

Lời giải

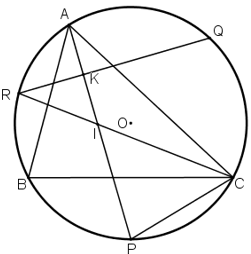
Bài 7: Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.

a) Chứng minh AP ⊥ QR.

b) AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.

Lời giải

a) Gọi K là giao điểm của QR và AP.

 là góc có đỉnh K nằm bên trong đường tròn

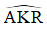
⇒ AP ⊥ QR.

+ R, P lần lượt là điểm chính giữa các cung 

⇒ ΔPCI cân tại P.

Bài 8: Cho đường tròn (O) và hai dây cung song song AB, CD (A và C nằm trong cùng một nửa mặt phẳng bờ BD); AD cắt BC tại I. Chứng minh:

Lời giải