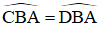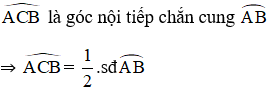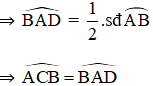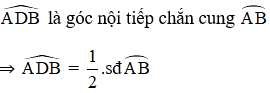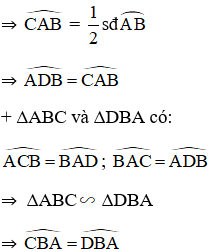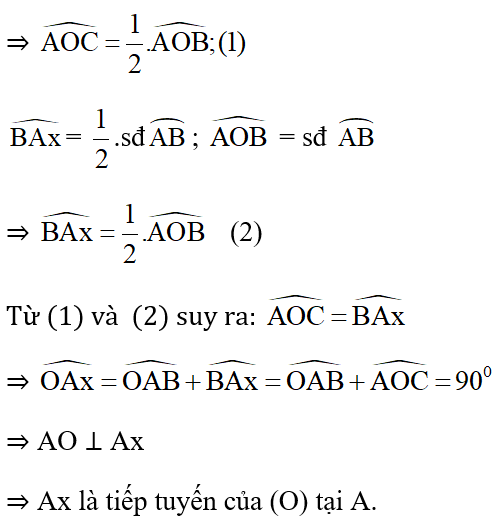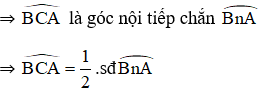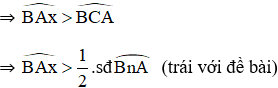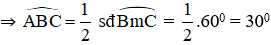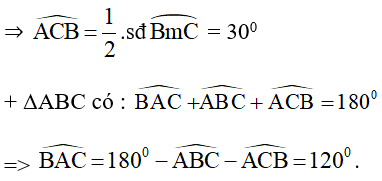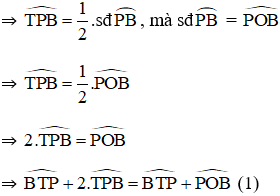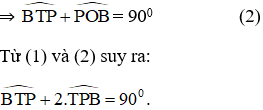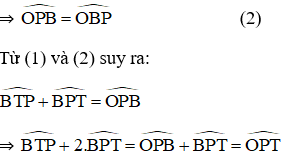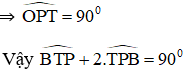50 Bài tập Góc tạo bởi tia tiếp tuyến và dây cung (có đáp án năm 2024) - Toán 9

Góc tạo bởi tia tiếp tuyến và dây cung

Kiến thức cần nhớ 

1. Định nghĩa

-  Góc tạo bởi tia tiếp tuyến và dây cung là góc có đỉnh nằm trên đường tròn, một cạnh là một tia tiếp tuyến còn cạnh kia chứa dây cung của đường tròn.

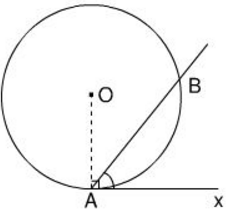
Ví dụ 1. Cho đường tròn (O) có xy là tiếp tuyến của đường tròn (O) tại A và dây cung AB như hình vẽ.

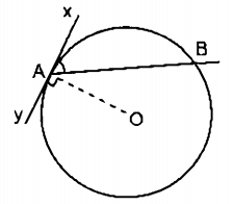
Ta thấy $\widehat{BAx}$ có đỉnh A nằm trên đường tròn (O) có Ax là tiếp tuyến và AB là dây cung của đường tròn.

Do đó $\widehat{BAx}$ là góc tạo bởi tiếp tuyến và dây cung.

Khi đó, $\widehat{BAx}$ chắn cung nhỏ AB;

$\widehat{BAy}$ chắn cung lớn AB.

2. Định lí

Số đo của góc tạo bởi tiếp tuyến và dây cung bằng nửa số đo của cung bị chắn.

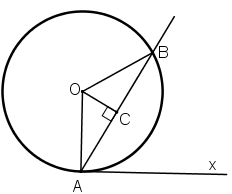
Ví dụ 2. Cho đường tròn (O) có xy là tiếp tuyến của đường tròn (O) tại A và dây cung AB như hình vẽ.

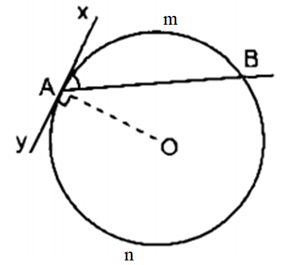
Khi đó, $\widehat{BAx}$ và $\widehat{BAy}$ là góc tạo bởi tiếp tiếp và dây cung lần lượt chắn $\widehat{AmB}$ và $\widehat{AnB}$. Do đó,

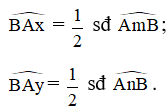
3. Hệ quả

Trong một đường tròn, góc tạo bởi tia tiếp tuyến và dây cung và góc nội tiếp cùng chắn một cung thì bằng nhau.

Ví dụ 2. Cho đường tròn (O) như hình vẽ.

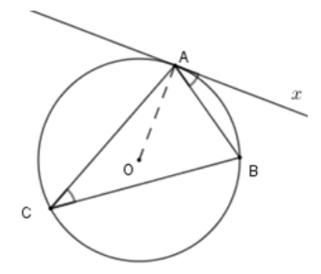
Trong hình vẽ trên, $\widehat{ACB}$ là góc nội tiếp chắn $\stackrel{⏜}{AB}$ nên

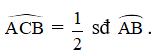
$\widehat{BAx}$ là góc tạo bởi dây cung và tiếp tuyến chắn $\stackrel{⏜}{AB}$ nên  

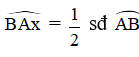
Bài tập tự luyện (có đáp án)

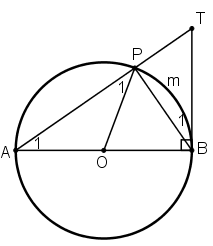
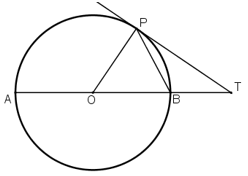
Bài 1: Cho đường tròn tâm O, đường kính AB. Lấy điểm P khác A và B trên đường tròn. Gọi T là giao điểm của AP với tiếp tuyến tại B của đường tròn. Chứng minh

Lời giải

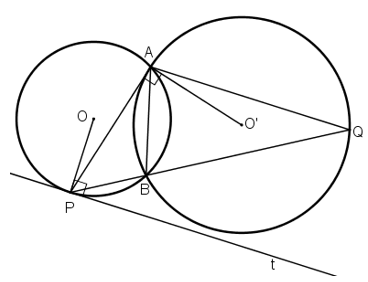
Bài 2: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến tại A của đường tròn (O') cắt đường tròn (O) tại điểm thứ hai P. Tia PB cắt đường tròn (O') tại Q. Chứng minh đường thẳng AQ song song với tiếp tuyến tại P của đường tròn (O).

Lời giải

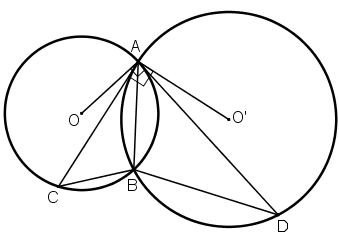
Bài 3: Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A đối với đường tròn (O') cắt (O) tại C và đối với đường tròn (O) cắt (O') tại D. Chứng minh 

Lời giải

+ Trên đường tròn tâm O:

 là góc tạo bởi tiếp tuyến AD và dây AB

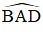
+ Trên đường tròn tâm O’:

 là góc tạo bởi tiếp tuyến AC và dây AB

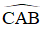
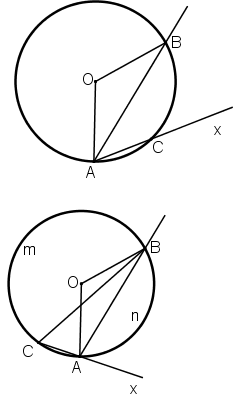
Bài 4: Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).

Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.

Hình 29

Lời giải

Cách 1: (Chứng minh trực tiếp)

Gọi C là chân đường cao hạ từ O xuống AB.

ΔOAB có OA = OB = R nên tam giác này cân tại O

⇒ đường cao OC đồng thời là phân giác

Cách 2: (Chứng minh phản chứng)

Giả sử Ax không phải tiếp tuyến của (O)

⇒ Ax là cắt (O) tại C khác A.

+ C nằm trên cung nhỏ AB

+ C nằm trên cung lớn AB

Mà 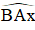 là góc ngoài của tam giác BAC

Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.

Bài 5: Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau ở A. Tính: 

Lời giải

+ ΔOBC có OB = OC = BC (= R)

⇒ ΔOBC là tam giác đều

+  là góc tạo bởi tiếp tuyến BA và dây BC

+  là góc tạo bởi tiếp tuyến AC và dây CB

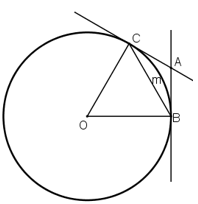
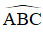
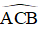
Bài 6: Cho đường tròn tâm O đường kính AB. Một tiếp tuyến của đường tròn tại P cắt đường thẳng AB tại T (điểm B nằm giữa O và T). Chứng minh:

Lời giải

Cách 1:

+  là góc tạo bởi tiếp tuyến PT và dây PB

+ PT là tiếp tuyến của đường tròn (O)

⇒ PT ⊥ OP

⇒ ΔOPT vuông tại P

Cách 2:

ΔPBT có: 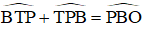 (định lý góc ngoài tam giác) (1)

ΔOPB có OP = OB (= R)

⇒ ΔOPB cân tại O

PT là tiếp tuyến của đường tròn (O)

⇒ PT ⊥ OP

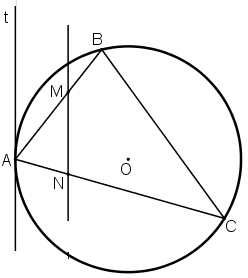
Bài 7: Cho A, B, C là ba điểm trên một đường tròn, At là tiếp tuyến của đường tròn tại A. Đường thẳng song song với At cắt AB tại M và cắt AC tại N. Chứng minh AB.AM = AC.AN.

Lời giải

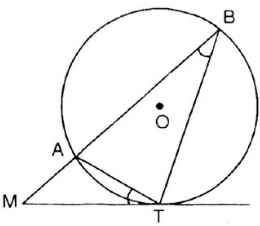
Bài 8: Cho đường tròn (O) và điểm M nằm bên ngoài đường tròn đó. Qua điểm M kẻ tiếp tuyến MT và cát tuyến MAB.

Chứng minh MT² = MA.MB.

Lời giải

( góc tạo bởi tia tiếp tuyến và dây cung, góc nội tiếp cùng chắn cung AT)

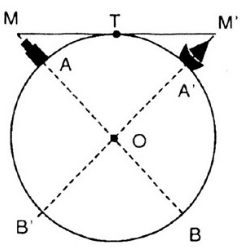
Bài 9: Trên bờ biển có một ngọn hải đăng cao 40m. Với khoảng cách bao nhiêu kilomet thì người quan sát trên tàu bắt đầu trông thấy ngọn đèn này, biết rằng mắt người quan sát ở độ cao 10m so với mực nước biển và bán kính Trái Đất gần bằng 6400km (h.30)?

Hướng dẫn: Áp dụng kết quả của bài tập 34.

Lời giải

Áp dụng kết quả bài 34 ta có:

+ MT² = MA.MB

MA = 40m = 0,04km ;

MB = MA + AB = MA + 2R = 12800,04 km.

⇒ MT ≈ 22,63 km

+ M’T² = M’A’.M’B’

M’A’ = 10m = 0,01km ;

M’B’ = M’A’ + A’B’ = M’A’ + 2R = 12800,01 km

⇒ M’T ≈ 11,31 km

⇒ MM’ = MT + M’T = 33,94 ≈ 34 km .

Vậy khi cách ngọn hải đăng khoảng 34km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.

Xem thêm các dạng bài tập toán hay khác:

150 Bài tập phương trình đường thẳng (2024) có đáp án

2000 Bài tập Toán 10 phương pháp tọa độ trong mặt phẳng (có đáp án năm 2023)

250 Bài tập đường tròn trong mặt phẳng tọa độ (có đáp án năm 2023)

90 Bài tập về Vị trí tương đối giữa hai đường thẳng, góc và khoảng cách (2024) có đáp án

100 Bài tập về Phương trình quy về phương trình bậc hai (có đáp án năm 2023)