50 Bài tập Một số hệ thức về cạnh và đường cao trong tam giác vuông
I. Kiến thức cần nhớ
1. Hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền
Định lí 1. Trong một tam giác vuông, bình phương mỗi cạnh góc vuông bằng tích của cạnh huyền và hình chiếu của cạnh góc vuông đó trên cạnh huyền.
Ví dụ 1. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
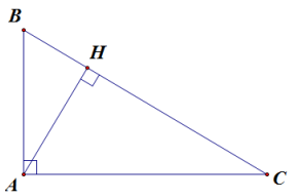
Ta có: AB2 = BC . BH; AC2 = BC . HC.
2. Một số hệ thức liên quan tới đường cao
Định lí 2. Trong một tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên cạnh huyền.
Ví dụ 2. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
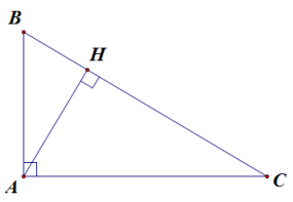
Ta có: AH2 = BH . HC.
Định lí 3. Trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
Ví dụ 3. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
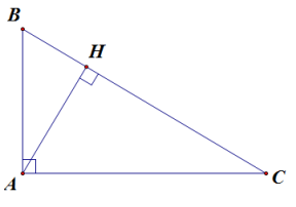
Ta có: AB . AC = BC . AH.
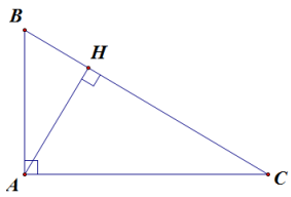
Định lí 4. Trong một tam giác vuông, nghịch đảo của bình phương đường cao ứng với cạnh huyền bằng tổng các nghịch đảo của bình phương hai cạnh góc vuông.
Ví dụ 4. Tam giác ABC vuông tại A, đường cao AH.
Khi đó, BH và CH lần lượt là hình chiếu của AB và AC trên BC.
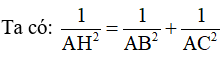
II. Bài tập tự luyện
Bài 1: Xét hình 1. Chứng minh . Từ đó suy ra hệ thức (2)
Hướng dẫn giải
Ta có:
Mà
Xét tam giác AHB và tam giác CHA có:
Vậy trong tam giác vuông, bình phương đường cao ứng với cạnh huyền bằng tích hai hình chiếu của hai cạnh góc vuông trên hai cạnh huyền.
Bài 2:
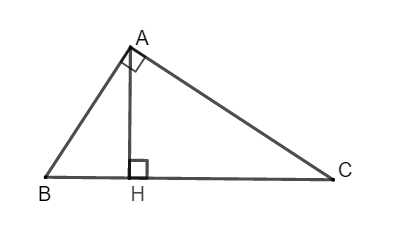
Xét hình 1. Hãy chứng minh hệ thức (3) bằng tam giác đồng dạng.
Hướng dẫn giải
Xét tam giác ABD và tam giác CAB có:
chung
Vậy ta có trong một tam giác vuông, tích hai cạnh góc vuông bằng tích của cạnh huyền và đường cao tương ứng.
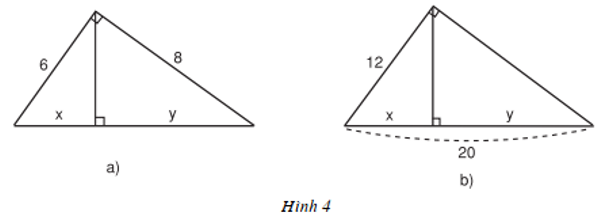
Bài 3: Hãy tính x và y trong mỗi hình sau (h.4a, b):
Hướng dẫn giải
a)
Áp dụng định lí Py-ta-go ta có:
(x + y)2 = 62 + 82
⇔ (x + y)2 = 100
⇒ x + y = 10
Áp dụng định lí (1) ta có:
62 = x.10 ⇔ x = 6210 = 3,6
82 = y.10 ⇔ y = 8210 = 6,4.
b)
Áp dụng định lí (1) có:
122 = x.20 ⇔ x = 12220 = 7,2
=> y = 20 - x = 20 -7,2 = 12,8.
Bài 4: Hãy tính x và y trong hình dưới đây:
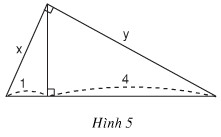
Hướng dẫn giải
Từ đề bài ta có cạnh huyền của tam giác có độ lớn là: 1 + 4 = 5
Áp dụng hệ thức lượng trong tam giác vuông đó là bình phương cạnh góc vuông bằng cạnh huyền nhân hình chiếu của cạnh ấy trên cạnh huyền, ta được:
Bài 5: Hãy tính x và y trong hình sau:
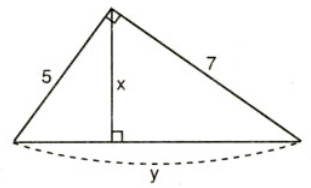
Hướng dẫn giải
Xét vuông tại A. Theo định lí Pytago, ta có:
Áp dụng hệ thức liên quan đến đường cao trong tam giác vuông, ta có:
Vậy
Bài 6:
Hãy tính x và y trong hình sau:
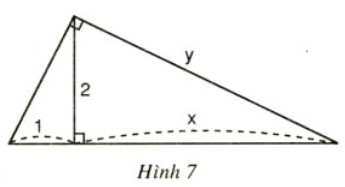
Hướng dẫn giải
Áp dụng định lí (2) ta có:
22 = 1 . x ⇒ x = 22 = 4.
Áp dụng định lí (1) ta có:
y2 = x. (x + 1)
=> y2 = 4.(4 + 1) = 20
=> y = √20 = 2√5.
Xem thêm các dạng bài tập hay, có đáp án:
Cách chứng minh tam giác vuông cân (2024) chi tiết nhất
Tính chất trọng tâm tứ diện (2024) chi tiết, có bài tập và đáp án
30 bài tập về tính chất tứ diện đều (2024) đầy đủ, có đáp án
50 Bài tập Hình tam giác - Diện tích hình tam giác (có đáp án năm 2024) - Toán lớp 5
60 Bài tập về Tính chất đường phân giác của tam giác (có đáp án năm 2023) - Toán 8