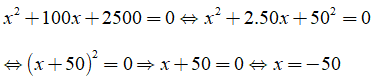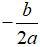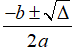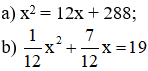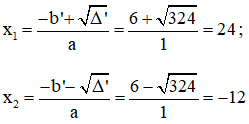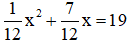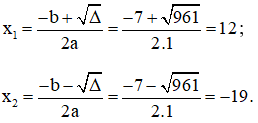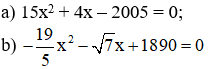50 Bài tập Công thức nghiệm thu gọn (có đáp án năm 2024) - Toán 9

Kiến thức cần nhớ 

Công thức nghiệm thu gọn

a) Biệt thức $∆\text{'}$

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và b = 2b’ ta có biệt thức  như sau:

$∆\text{'}$= $\mathrm{b}{\text{'}}^2-\mathrm{ac}$

Ta sửa dụng biết thức $∆\text{'}$để giải phương trình bậc hai.

b) Công thức nghiệm thu gọn của phương trình bậc hai

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) có b = 2b’ và biệt thức $∆\text{'}$= b’² - ac

+ Nếu  > 0 thì phương trình có hai nghiệm phân biệt là

${\mathrm{x}}_1=\frac{-\mathrm{b}+\sqrt{∆\text{'}}}{\mathrm{a}}; {\mathrm{x}}_2=\frac{-\mathrm{b}+\sqrt{∆\text{'}}}{\mathrm{a}}$

+ Nếu  = 0 thì phương trình có nghiệm kép là

${\mathrm{x}}_1={\mathrm{x}}_2=\frac{-\mathrm{b}}{\mathrm{a}}$

+ Nếu  < 0 thì phương trình vô nghiệm.

Ví dụ minh họa

Câu 1: Nghiệm của phương trình x² + 100x + 2500 = 0 là?

A. 50

B. -50

C. ± 50

D. ± 100

Lời giải:

Ta có:

Chọn đáp án B.

Câu 2: Cho phương trình ax² + bx + c = 0 (a ≠ 0) có biệt thức Δ = b² - 4ac. Phương trình đã cho vô nghiệm khi:

A. Δ < 0

B. Δ = 0

C. Δ ≥ 0

D. Δ ≤ 0

Lời giải:

Xét phương trình bậc hai một ẩn ax² + bx + c = 0 (a ≠ 0) và biệt thức Δ = b² - 4ac

• TH1: Nếu thì phương trình vô nghiệm

• TH2: Nếu thì phương trình có nghiệm kép x₁ = x₂ = 

• TH3: Nếu thì phương trình có hai nghiệm phân biệt x_1,2 = 

Chọn đáp án A.

Bài tập tự luyện 

Bài 1: Xác định a, b', c rồi dùng công thức nghiệm thu gọn giải các phương trình:

a) 4x² + 4x + 1 = 0 ;

b) 13852x² – 14x + 1 = 0;

c) 5x² – 6x + 1 = 0;

d) $-3x^2+4\sqrt{6}x+4=0$

Lời giải

a) $4x^2+4x+1=0$

Có a = 4; b’ = 2; c = 1;

Δ’ = (b’)² – ac = 2² – 4.1 = 0

Phương trình có nghiệm kép là:

$x_1=x_2=\frac{-b\text{'}}{a}=\frac{-2}{4}=\frac{-1}{2}$

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{-1}{2}\right\}$

b) $13852x^2-14x+1=0$

Có a = 13852; b’ = -7; c = 1; 

Δ’ = (b’)² – ac = (-7)² – 13852.1 =49 – 13852 = -13803 < 0

Vậy phương trình vô nghiệm.

c) $5x^2-6x+1=0$

Có: a = 5; b’ = -3; c = 1; 

Δ’ = (b’)² – ac = (-3)² – 5.1 = 9 – 5 = 4 > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{3+\sqrt{4}}{5}=\frac{3+2}{5}=1$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{3-\sqrt{4}}{5}=\frac{3-2}{5}=\frac{1}{5}$

Vậy phương trình đã cho có nghiệm $S=\left\{\frac{1}{5};1\right\}$

d) $-3x^2+4\sqrt{6}x+4=0$

a = -3; b’ = $2\sqrt{6}$; c = 4

$\Delta \text{'}={\left(b\text{'}\right)}^2-ac={\left(2\sqrt{6}\right)}^2-\left(-3\right).4=36$ > 0 

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{-2\sqrt{6}+\sqrt{36}}{-3}=\frac{-2\sqrt{6}+6}{-3}=\frac{-6+2\sqrt{6}}{3}$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{-2\sqrt{6}-\sqrt{36}}{-3}=\frac{-2\sqrt{6}-6}{-3}=\frac{6+2\sqrt{6}}{3}$

Vậy phương trình đã cho có nghiệm $S=\left\{\frac{-6+2\sqrt{6}}{3};\frac{6+2\sqrt{6}}{3}\right\}$

Bài 2: Đưa các phương trình sau về dạng ax² + 2b'x + c = 0 và giải chúng. Sau đó, dùng bảng số hoặc máy tính để viết gần đúng nghiệm tìm được (làm tròn kết quả đến chữ số thập phân thứ hai):

a) 3x² – 2x = x² + 3;

b) (2x - √2)² – 1 = (x + 1)(x – 1);

c) 3x² + 3 = 2(x + 1);

d) 0,5x(x + 1) = (x – 1)².

Lời giải

a) 3x² – 2x = x² + 3

⇔ 3x² – 2x – x² – 3 = 0

⇔ 2x² – 2x – 3 = 0 (*)

Có a = 2; b’ = -1; c = -3; Δ’ = b’² – ac = (-1)² – 2.(-3) = 7 > 0

Phương trình (*) có hai nghiệm phân biệt:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{1+\sqrt{7}}{2}\approx 1,82$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{1-\sqrt{7}}{2}\approx -0,82$

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{1-\sqrt{7}}{2};\frac{1+\sqrt{7}}{2}\right\}$

b)${\left(2x-\sqrt{2}\right)}^2$ – 1 = (x + 1)(x – 1);

⇔ 4x² – 2.2x.$\sqrt{2}$ + 2 – 1 = x² – 1

⇔ 4x² – 2.2$\sqrt{2}$.x + 2 – 1 – x² + 1 = 0

⇔ 3x² – 2.2$\sqrt{2}$.x + 2 = 0

Có: a = 3; b’ = -2$\sqrt{2}$; c = 2; Δ’ = b’² – ac =${\left(-2\sqrt{2}\right)}^2$ – 3.2 = 8 – 6 = 2 > 0

Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{2\sqrt{2}+\sqrt{2}}{3}=\frac{3\sqrt{2}}{3}=\sqrt{2}\approx 1,41$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{2\sqrt{2}-\sqrt{2}}{3}=\frac{\sqrt{2}}{3}\approx 0,47$

Vậy phương trình đã cho có tập nghiệm $S=\left\{\sqrt{2};\frac{\sqrt{2}}{3}\right\}$

c) 3x² + 3 = 2(x + 1)

⇔ 3x² + 3 = 2x + 2

⇔ 3x² + 3 – 2x – 2 = 0

⇔ 3x² – 2x + 1 = 0

Phương trình có a = 3; b’ = -1; c = 1; Δ’ = b’² – ac = (-1)² – 3.1 = -2 < 0

Vậy phương trình đã cho vô nghiệm.

d) 0,5x(x + 1) = (x – 1)²

⇔ 0,5x² + 0,5x = x² – 2x + 1

⇔ x² – 2x + 1 – 0,5x² – 0,5x = 0

⇔ 0,5x² – 2,5x + 1 = 0

⇔ x² – 5x + 2 = 0

Có a = 1; b’ = $\frac{-5}{2}$; c = 2;$\Delta \text{'}=b{\text{'}}^2-ac={\left(\frac{-5}{2}\right)}^2-1.2=\frac{25}{4}-2=\frac{17}{4}$ > 0

Vì Δ’ > 0 nên phương trình có hai nghiệm phân biệt là:

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{\frac{5}{2}+\sqrt{\frac{17}{4}}}{1}=\frac{5+\sqrt{17}}{2}\approx 4,56$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{\frac{5}{2}-\sqrt{\frac{17}{4}}}{1}=\frac{5-\sqrt{17}}{2}\approx 0,44$

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{5+\sqrt{17}}{2};\frac{5-\sqrt{17}}{2}\right\}$

Bài 3: Đố: Đố em biết vì sao khi a > 0 và phương trình ax² + bx + c = 0 vô nghiệm thì ax² + bx + c > 0 với mọi giá trị của x?

Lời giải

Ta có: $a{x}^2+bx+c=a\left(x^2+\frac{b}{a}x\right)+c$

= $a\left[x^2+2.x.\frac{b}{2a}+{\left(\frac{b}{2a}\right)}^2-{\left(\frac{b}{2a}\right)}^2\right]+c$

= $a\left[{\left(x+\frac{b}{2a}\right)}^2-\frac{b^2}{4a^2}\right]+c$

= $a{\left(x+\frac{b}{2a}\right)}^2-\frac{b^2}{4a}+c$

$=a{\left(x+\frac{b}{2a}\right)}^2-\frac{b^2-4ac}{4a}$

Ta có: a > 0 (giả thuyết) và ${\left(x+\frac{b}{2a}\right)}^2\ge 0$ với mọi x, a, b

$\Rightarrow a{\left(x+\frac{b}{2a}\right)}^2\ge 0$ với mọi a > 0; x, b tùy ý.   (1)

Phương trình ax² + bx + c = 0 vô nghiệm nên:

$\Delta =b^2-4ac<0$

Do a > 0 nên $\frac{b^2-4ac}{4a}<0$

$\Rightarrow -\frac{b^2-4ac}{4a}>0$ (2)

Từ (1) và (2) ta có:

$a{x}^2+bx+c=a{\left(x+\frac{b}{2a}\right)}^2-\frac{b^2-4ac}{4a}>0$ với mọi x.

Bài 4: Giải các phương trình:

a) 25x² – 16 = 0;

b) 2x² + 3 = 0;

c) 4,2x² + 5,46x = 0;

d) 4x² - 2√3.x = 1 - √3.

Lời giải

Cách 1: 

a) 25x² – 16 = 0

$\iff {\left(5x\right)}^2-4^2=0$

$\iff \left(5x-4\right)\left(5x+4\right)=0$

$\iff \left[\begin{array}{l}5x-4=0\\ 5x+4=0\end{array}\right.$

$\iff \left[\begin{array}{l}5x=4\\ 5x=-4\end{array}\right.$

$\iff \left[\begin{array}{l}x=\frac{4}{5}\\ x=\frac{-4}{5}\end{array}\right.$

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{4}{5};\frac{-4}{5}\right\}$.

b) 2x² + 3 = 0

Ta có: a = 2; b = 0; c = 3

$\Delta =b^2-4.a.c=0^2-\mathrm{4.2.3}=-24<0$

Vậy phương trình đã cho vô nghiệm.

c) 4,2x² + 5,46x = 0

Ta có: a = 4,2; b = 5,46; c = 0

$\Delta =b^2-ac=5,{46}^2-\mathrm{4.4.2.0}=5,{46}^2$ > 0

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-5,46+\sqrt{5,{46}^2}}{2.4,2}=0$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-5,46-\sqrt{5,{46}^2}}{2.4,2}=\frac{-13}{10}$

Vậy phương trình đã cho có nghiệm $S=\left\{0;\frac{-13}{10}\right\}$.

d) 4x² - 2$\sqrt{3}$.x = 1 - $\sqrt{3}$

$\iff 4x^2-2\sqrt{3}x-1+\sqrt{3}=0$

Ta có: a = 4; b’ = $-\sqrt{3}$; c = -1 + $\sqrt{3}$

$\Delta \text{'}=b{\text{'}}^2-ac={\left(-\sqrt{3}\right)}^2-4.\left(-1+\sqrt{3}\right)$

$\iff$ $\Delta \text{'}=7-4\sqrt{3}=2^2-\mathrm{2.2.}\sqrt{3}+{\left(\sqrt{3}\right)}^2$

$\iff \Delta \text{'}={\left(2-\sqrt{3}\right)}^2$ > 0 $\Rightarrow \sqrt{\Delta \text{'}}=\sqrt{{\left(2-\sqrt{3}\right)}^2}=2-\sqrt{3}$

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b\text{'}+\sqrt{\Delta \text{'}}}{a}=\frac{\sqrt{3}+2-\sqrt{3}}{4}=\frac{2}{4}=\frac{1}{2}$

$x_2=\frac{-b\text{'}-\sqrt{\Delta \text{'}}}{a}=\frac{\sqrt{3}-2+\sqrt{3}}{4}=\frac{2\sqrt{3}-2}{4}=\frac{\sqrt{3}-1}{2}$

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{\sqrt{3}-1}{2};\frac{1}{2}\right\}$

Bài 5: Giải vài phương trình của An Khô-va-ri-zmi (xem Toán 7, Tập 2, tr.26):

Lời giải

a) x² = 12x + 288

⇔ x² – 12x – 288 = 0

Có a = 1; b’ = -6; c = -288; Δ’ = b’² – ac = (-6)² – 1.(-288) = 324 > 0

Phương trình có hai nghiệm:

Vậy phương trình có hai nghiệm x₁ = 24 và x₂ = -12.

b) 

⇔ x² + 7x = 228

⇔ x² + 7x – 228 = 0

Có a = 1; b = 7; c = -228; Δ = b² – 4ac = 7² – 4.1.(-228) = 961 > 0

Phương trình có hai nghiệm:

Vậy phương trình có hai nghiệm x₁ = 12 và x₂ = -19.

Bài 6: Không giải phương trình, hãy cho biết mỗi phương trình sau có bao nhiêu nghiệm?

Lời giải

a) Phương trình 15x² + 4x – 2005 = 0 có a = 15; c = -2005 trái dấu

⇒ Phương trình có hai nghiệm phân biệt.

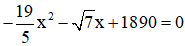
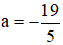
b) Phương trình  có  ; c = 1890 trái dấu

⇒ Phương trình có hai nghiệm phân biệt.

Bài 7: Rada của một máy bay trực thăng theo dõi chuyển động của ôtô trong 10 phút, phát hiện rằng vận tốc v của ôtô thay đổi phụ thuộc vào thời gian bởi công thức:

v = 3t² -30t + 135

(t tính bằng phút, v tính bằng km/h)

a) Tính vận tốc của ôtô khi t = 5 phút.

b) Tính giá trị của t khi vận tốc ôtô bằng 120km/h (làm tròn kết quả đến chữ số thập phân thứ hai).

Lời giải

a) Tại t = 5, ta có: v = 3.5² – 30.5 + 135 = 60 (km/h)

b) Khi v = 120 km/h

⇔ 3t² – 30t + 135 = 120

⇔ 3t² – 30t + 15 = 0

Có a = 3; b’ = -15; c = 15; Δ’ = b’² – ac = (-15)² – 3.15 = 180

Phương trình có hai nghiệm phân biệt

Vì rada quan sát chuyển động của ô tô trong 10 phút nên t₁ và t₂ đều thỏa mãn.

Vậy tại t = 9,47 phút hoặc t = 0,53 phút thì vận tốc ô tô bằng 120km/h.

Bài 8: Cho phương trình (ẩn x) x² – 2(m – 1)x + m² = 0.

a) Tính Δ'.

b) Với giá trị nào của m thì phương trình có hai nghiệm phân biệt? Có nghiệm kép? Vô nghiệm.

Lời giải

a) Phương trình x² – 2(m – 1)x + m² = 0 (1)

Có a = 1; b’ = -(m – 1); c = m²

⇒ Δ’ = b'² – ac = (1 – m)² – 1.m² = 1 – 2m + m² – m² = 1 – 2m.

b) Phương trình (1):

+ Vô nghiệm ⇔ Δ’ < 0 ⇔ 1 – 2m < 0 ⇔ 2m > 1 ⇔ m > 

+ Có nghiệm kép ⇔ Δ’ = 0 ⇔ 1 – 2m = 0 ⇔ m = 

+ Có hai nghiệm phân biệt ⇔ Δ’ > 0 ⇔ 1 – 2m > 0 ⇔ 2m < 1 ⇔ m < 

Vậy: Phương trình (1) có hai nghiệm phân biệt khi m < 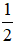; có nghiệm kép khi m =  và vô nghiệm khi m > 

Xem thêm các dạng bài tập khác:

50 Bài tập Công thức nghiệm của phương trình bậc hai (có đáp án năm 2024)

30 Bài tập về Công thức nghiệm của phương trình bậc hai (2024)

Công thức nghiệm (2024)

40 Bài tập Phương trình quy về phương trình bậc nhất, bậc hai (2024)

50 Bài tập Phương trình quy về phương trình bậc hai (có đáp án năm 2024)