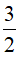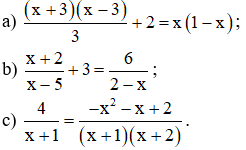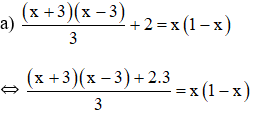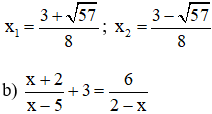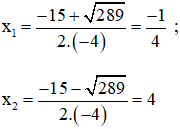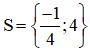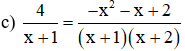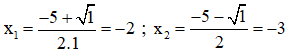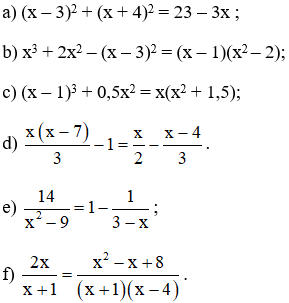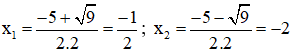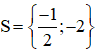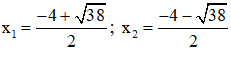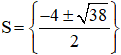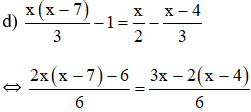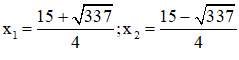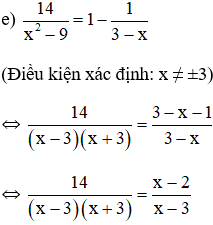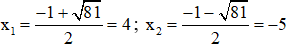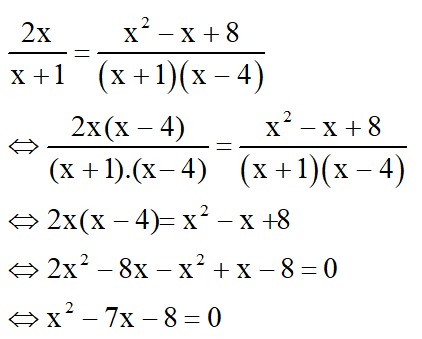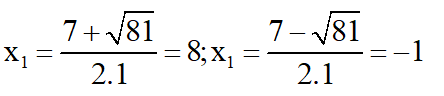40 Bài tập Phương trình quy về phương trình bậc nhất, bậc hai (2024) cực hay, có đáp án

Các dạng phương trình quy về phương trình bậc hai

ÔN TẬP VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI

1. Phương trình bậc nhất

Cách giải và biện luận phương trình dạng ax + b = 0 được tóm tắt trong bảng sau

Khi a ≠ 0 phương trình ax + b = 0 được gọi là phương trình bậc nhất một ẩn.

2. Phương trình bậc hai

Cách giải và công thức nghiệm của phương trình bậc hai được tóm tắt trong bảng sau

3. Định lí Vi–ét

Nếu phương trình bậc hai ax² + bx + c = 0 (a ≠ 0) có hai nghiệm x₁, x₂ thì

x₁ + x₂ = - , x₁x₂ = .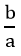

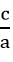
Ngược lại, nếu hai số u và v có tổng u + v = S và tích uv = P thì u và v là các nghiệm của phương trình

x² – Sx + P = 0.

PHƯƠNG TRÌNH QUY VỀ PHƯƠNG TRÌNH BẬC NHẤT, BẬC HAI

Có nhiều phương trình khi giải có thể biến đổi về phương trình bậc nhất hoặc bậc hai.

Sau đây ta xét hai trong các dạng phương trình đó.

1. Phương trình chứa ẩn trong dấu giá trị tuyệt đối

Để giải phương trình chứa ẩn trong dấu giá trị tuyệt đối ta có thể dùng định nghĩa của giá trị tuyệt đối hoặc bình phương hai vế để khử dấu giá trị tuyệt đối.

Ví dụ 1. Giải phương trình |x – 3| = 2x + 1. (3)

Hướng dẫn giải

Cách 1

a) Nếu x ≥ 3 thì phương trình (3) trở thành x – 3 = 2x + 1. Từ đó x = –4.

Giá trị x = –4 không thỏa mãn điều kiện x ≥ 3 nên bị loại.

b) Nếu x < 3 thì phương trình (3) trở thành –x + 3 = 2x + 1. Từ đó x = .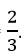

Giá trị này thỏa mãn điều kiện x < 3 nên là nghiệm.

Kết luận. Vậy nghiệm của phương trình là x = 

Cách 2. Bình phương hai vế của phương trình (3) ta đưa tới phương trình hệ quả

(3) => (x – 3)² = (2x + 1)²

=> x² – 6x + 9 = 4x² + 4x + 1

=> 3x² + 10x – 8 = 0.

Phương trình cuối có hai nghiệm là x = –4 và x = 

Thử lại ta thấy phương trình (3) chỉ có nghiệm là x = 

2. Phương trình chứa ẩn dưới dấu căn

Để giải các phương trình chứa ẩn dưới dấu căn bậc hai, ta thường bình phương hai vế để đưa về một phương trình hệ quả không chứa ẩn dưới dấu căn.

Ví dụ 2. Giải phương trình 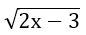 = x – 2 (4).

Hướng dẫn giải

Điều kiện của phương trình (4) là x ≥ 

Bình phương hai vế của phương trình (4) ta đưa tới phương trình hệ quả

(4) => 2x – 3 = x² – 4x + 4

=> x² – 6x + 7 = 0.

Phương trình cuối có hai nghiệm là x = 3 + √2 và x = 3 – √2 . Cả hai giá trị này đều thỏa mãn điều kiện của phương trình (4), nhưng khi thay vào phương trình (4) thì giá trị x = 3 – √2 bị loại (vế trái dương còn vế phải âm), còn giá trị x= 3 + √2 là nghiệm (hai vế cùng bằng √2 + 1).

Kết luận. Vậy nghiệm của phương trình (4) là x= 3 + √2 .

BÀI TẬP VẬN DỤNG (CÓ ĐÁP ÁN)

Bài 1: Giải các phương trình:

Lời giải

⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)

⇔ x² – 9 + 6 = 3x – 3x²

⇔ x² – 9 + 6 – 3x + 3x² = 0

⇔ 4x² – 3x – 3 = 0

Có a = 4; b = -3; c = -3 ⇒ Δ = (-3)² – 4.4.(-3) = 57 > 0

Phương trình có hai nghiệm

Điều kiện xác định: x ≠ 5; x ≠ 2.

Quy đồng và khử mẫu ta được :

(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)

⇔ 4 – x² + 6x – 3x² – 30 + 15x = 6x – 30

⇔ 4 – x² + 6x – 3x² – 30 + 15x – 6x + 30 = 0

⇔ -4x² + 15x + 4 = 0

Có a = -4; b = 15; c = 4 ⇒ Δ = 15² – 4.(-4).4 = 289 > 0

Phương trình có hai nghiệm phân biệt:

Cả hai giá trị đều thỏa mãn điều kiện.

Vậy phương trình có tập nghiệm 

Điều kiện xác định: x ≠ -1; x ≠ -2.

Quy đồng và khử mẫu ta được:

4.(x + 2) = -x² – x + 2

⇔ 4x + 8 = -x² – x + 2

⇔ 4x + 8 + x² + x – 2 = 0

⇔ x² + 5x + 6 = 0.

Có a = 1; b = 5; c = 6 ⇒ Δ = 5² – 4.1.6 = 1 > 0

⇒ Phương trình có hai nghiệm phân biệt:

Chỉ có nghiệm x₂ = -3 thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x = -3.

Bài 2: Giải các phương trình trùng phương:

a) x⁴ – 5x² + 4 = 0;

b) 2x⁴ – 3x² – 2 = 0;

c) 3x⁴ + 10x² + 3 = 0

Lời giải

a) x⁴ – 5x² + 4 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : t² – 5t + 4 = 0 (2)

Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm t₁ = 1; t₂ = $\frac{c}{a}=\frac{4}{1}$ = 4

Cả và thỏa mãn $t\ge 0$

+ Với t = 1 ⇒ x² = 1 ⇒ x = $\pm 1$

+ Với t = 4 ⇒ x² = 4 ⇒ x = $\pm 2$

Vậy phương trình đã cho có tập nghiệm $S=\left\{-2;-1;1;2\right\}$

b) 2x⁴ – 3x² – 2 = 0; (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : 2t² – 3t – 2 = 0 (2)

Giải (2) : Có a = 2 ; b = -3 ; c = -2

⇒ Δ = (-3)² - 4.2.(-2) = 25 > 0

⇒ Phương trình có hai nghiệm phân biệt

$t_1=\frac{3+\sqrt{25}}{2.2}=2;t_2=\frac{3-\sqrt{25}}{2.2}=\frac{-1}{2}$

Vì $t\ge 0$ nên chỉ có t = 2 thỏa mãn điều kiện

+ Với t = 2 ⇒ x² = 2 ⇒ x = $\pm \sqrt{2}$

Vậy phương trình đã cho có tập nghiệm $S=\left\{-\sqrt{2};\sqrt{2}\right\}$

c) 3x⁴ + 10x² + 3 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành: 3t² + 10t + 3 = 0 (2)

Giải (2) : Có a = 3; b' = 5; c = 3

⇒ Δ’ = 5² – 3.3 = 16 > 0

⇒ Phương trình có hai nghiệm phân biệt

$t_1=\frac{-5+\sqrt{16}}{3}=\frac{-1}{3};t_2=\frac{-5-\sqrt{16}}{3}=-3$

Vì $t\ge 0$ nên cả đều $t_1;t_2$ không thỏa mãn.

Bài 3: Giải các phương trình:

a) (3x² – 5x + 1)(x² – 4) = 0;

b) (2x² + x – 4)² – (2x – 1)² = 0.

Lời giải

a) (3x² – 5x + 1)(x² – 4) = 0

$\left[\begin{array}{l}3x^2-5x+1=0\text{ (1)}\\ x^2-4=0\text{ (2)}\end{array}\right.$

+ Giải (1): 3x² – 5x + 1 = 0

Có a = 3; b = -5; c = 1 ⇒ Δ = (-5)² – 4.3 = 13 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{5+\sqrt{13}}{2.3}=\frac{5+\sqrt{13}}{6}$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{5-\sqrt{13}}{2.3}=\frac{5-\sqrt{13}}{6}$

+ Giải (2): x² – 4 = 0 ⇔ x² = 4 ⇔ x = $\pm$2

Vậy phương trình ban đầu có tập nghiệm $S=\left\{-2;\frac{5-\sqrt{13}}{6};2;\frac{5+\sqrt{13}}{6}\right\}$

b) (2x² + x – 4)² – (2x – 1)² = 0

⇔ (2x² + x – 4 – 2x + 1)(2x² + x – 4 + 2x – 1) = 0

⇔ (2x² – x – 3)(2x² + 3x – 5) = 0

⇔ 2x² – x – 3 = 0 (1)

hoặc 2x² + 3x – 5 = 0 (2)

+ Giải (1): 2x² – x – 3 = 0

Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -$\frac{c}{a}$ = $\frac{3}{2}$.

+ Giải (2): 2x² + 3x – 5 = 0

Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm x = 1 và x = $\frac{c}{a}$ = -$\frac{5}{2}$.

Vậy phương trình có tập nghiệm S = $\left\{\frac{-5}{2};-1;1;\frac{3}{2}\right\}$

Bài 4: Giải phương trình trùng phương:

a)$9x^4-10x^2+1=0$

b)$5x^4+2x^2-16=10-x^2$

c)$0,3x^4+1,8x^2+1,5=0$

d)$2x^2+1=\frac{1}{x^2}-4$

Lời giải

a) 9x⁴ – 10x² + 1 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : 9t² – 10t + 1 = 0 (2)

Giải (2):

Có a = 9; b = -10; c = 1

⇒ a + b + c = 0

⇒ Phương trình (2) có nghiệm t₁ = 1; t₂ = $\frac{c}{a}=\frac{1}{9}$

Cả hai nghiệm đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ x² = 1 ⇒ x = $\pm 1$

+ Với t = $\frac{1}{9}\Rightarrow x=\pm \sqrt{\frac{1}{9}}=\pm \frac{1}{3}$.

Vậy phương trình có tập nghiệm $S=\left\{-1;\frac{-1}{3};\frac{1}{3};1\right\}$

b) 5x⁴ + 2x² – 16 = 10 – x²

⇔ 5x⁴ + 2x² – 16 – 10 + x² = 0

⇔ 5x⁴ + 3x² – 26 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : 5t² + 3t – 26 = 0 (2)

Giải (2) :

Có a = 5 ; b = 3 ; c = -26

⇒ Δ = 3² – 4.5.(-26) = 529 > 0

⇒ Phương trình có hai nghiệm phân biệt:

$t_1=\frac{-3+\sqrt{529}}{2.5}=2;t_2=\frac{-3-\sqrt{529}}{2.5}=\frac{-26}{10}$

Đối chiếu điều kiện $t\ge 0$ chỉ có t₁ = 2 thỏa mãn

+ Với t = 2 ⇒ x² = 2 ⇒ x = $\pm \sqrt{2}$

Vậy phương trình (1) có tập nghiệm S = $\left\{-\sqrt{2};\sqrt{2}\right\}$

c) 0,3x⁴ + 1,8x² + 1,5 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó, (1) trở thành : 0,3t² + 1,8t + 1,5 = 0 (2)

Giải (2) :

Ta có: a = 0,3 ; b = 1,8 ; c = 1,5

⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm t₁ = -1 và t₂ = $\frac{-c}{a}=\frac{-1,5}{0,3}=-5$

Cả hai nghiệm đều không thỏa mãn điều kiện $t\ge 0$.

Vậy phương trình (1) vô nghiệm.

d) Điều kiện xác định: x ≠ 0.

$2x^2+1=\frac{1}{x^2}-4$

$\iff \frac{2x^4}{x^2}+\frac{x^2}{x^2}=\frac{1}{x^2}-\frac{4x^2}{x^2}$

2x⁴ + x² = 1 – 4x²

⇔ 2x⁴ + x² + 4x² – 1 = 0

⇔ 2x⁴ + 5x² – 1 = 0 (1)

Đặt t = x², điều kiện t > 0.

Khi đó (1) trở thành : 2t² + 5t – 1 = 0 (2)

Giải (2) :

Có a = 2 ; b = 5 ; c = -1

⇒ Δ = 5² – 4.2.(-1) = 33 > 0

⇒ Phương trình có hai nghiệm phân biệt:

$t_1=\frac{-5+\sqrt{33}}{4};t_2=\frac{-5-\sqrt{33}}{4}$

Đối chiếu với điều kiện t > 0 thấy có nghiệm t₁ thỏa mãn.

+ Với t = $\frac{-5+\sqrt{33}}{4}\Rightarrow x^2=\frac{-5+\sqrt{33}}{4}$

$\Rightarrow x=\pm \sqrt{\frac{-5+\sqrt{33}}{4}}=\pm \frac{\sqrt{-5+\sqrt{33}}}{2}$ (thỏa mãn)

Vậy phương trình có tập nghiệm S = $\left\{\pm \frac{\sqrt{-5+\sqrt{33}}}{2}\right\}$

Bài 5: Giải các phương trình:

Lời giải

a) (x – 3)² + (x + 4)² = 23 – 3x

⇔ x² – 6x + 9 + x² + 8x + 16 = 23 – 3x

⇔ x² – 6x + 9 + x² + 8x + 16 + 3x – 23 = 0

⇔ 2x² + 5x + 2 = 0

Có a = 2; b = 5; c = 2 ⇒ Δ = 5² – 4.2.2 = 9 > 0

⇒ Phương trình có hai nghiệm:

Vậy phương trình có tập nghiệm 

b) x³ + 2x² – (x – 3)² = (x – 1)(x² – 2)

⇔ x³ + 2x² – (x² – 6x + 9) = x³ – x² – 2x + 2

⇔ x³ + 2x² – x² + 6x – 9 – x³ + x² + 2x – 2 = 0

⇔ 2x² + 8x – 11 = 0.

Có a = 2; b = 8; c = -11 ⇒ Δ’ = 4² – 2.(-11) = 38 > 0

⇒ Phương trình có hai nghiệm:

Vậy phương trình có tập nghiệm 

c) (x – 1)³ + 0,5x² = x(x² + 1,5)

⇔ x³ - 3x² + 3x – 1 + 0,5x² = x³ + 1,5x

⇔ x³ + 1,5x – x³ + 3x² – 3x + 1 – 0,5x² = 0

⇔ 2,5x² – 1,5x + 1 = 0

Có a = 2,5; b = -1,5; c = 1

⇒ Δ = (-1,5)² – 4.2,5.1 = -7,75 < 0

Vậy phương trình vô nghiệm.

⇔ 2x(x – 7) – 6 = 3x – 2(x – 4)

⇔ 2x² – 14x – 6 = 3x – 2x + 8

⇔ 2x² – 14x – 6 – 3x + 2x – 8 = 0

⇔ 2x² – 15x – 14 = 0.

Có a = 2; b = -15; c = -14

⇒ Δ = (-15)² – 4.2.(-14) = 337 > 0

⇒ Phương trình có hai nghiệm:

⇔ 14 = (x – 2)(x + 3)

⇔ 14 = x² – 2x + 3x – 6

⇔ x² + x – 20 = 0

Có a = 1; b = 1; c = -20

⇒ Δ = 1² – 4.1.(-20) = 81 > 0

Phương trình có hai nghiệm:

Cả hai nghiệm đều thỏa mãn điều kiện xác định.

Vậy phương trình có tập nghiệm S = {-5; 4}.

f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8

∆ = (-7)² – 4.1. (- 8)= 81

=> Phương trình có hai nghiệm:

Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8

Bài 6: Giải phương trình bằng cách đặt ẩn phụ:

a) $3{\left(x^2+x\right)}^2-2\left(x^2+x\right)-1=0$

b) ${\left(x^2-4x+2\right)}^2+x^2-4x-4=0$

c) $x-\sqrt{x}=5\sqrt{x}+7$

d) $\frac{x}{x+1}-10.\frac{x+1}{x}=3$

Hướng dẫn:

a) Đặt t = x² + x, ta có phương trình 3t² - 2t - 1 = 0. Giải phương trình này, ta tìm được hai giá trị của t. Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x² +x, ta được một phương trình của ẩn x. Giải mỗi phương trình này sẽ tìm được giá trị của x.

d) Đặt $\frac{x+1}{x}=t$ hoặc $\frac{x}{x+1}=t$

Lời giải

a) $3{\left(x^2+x\right)}^2-2\left(x^2+x\right)-1=0$

Đặt $x^2+x=t$ khi đó phương trình trở thành:

$3t^2-2t-1=0$

Ta có: a = 3; b = -2; c = -1

Nhận thấy a + b + c = 0

Phương trình có hai nghiệm phân biệt: 

$t_1=1;t_2=\frac{c}{a}=\frac{-1}{3}$

+) Với t = 1 $\Rightarrow x^2+x=1$

$\iff x^2+x-1=0$

Ta có: a = 1; b = 1; c = -1

$\Delta =b^2-4ac=1^2-\mathrm{4.1.}\left(-1\right)=5$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-1+\sqrt{5}}{2};$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-1-\sqrt{5}}{2}$

+ Với t = $\frac{-1}{3}\Rightarrow x^2+x=\frac{-1}{3}$

$\iff x^2+x+\frac{1}{3}=0$

Ta có: a = 1; b = 1; c = $\frac{1}{3}$

$\Delta =1^2-\mathrm{4.1.}\frac{1}{3}=\frac{-1}{3}<0$$\Rightarrow$ vô nghiệm

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{-1-\sqrt{5}}{2};\frac{-1+\sqrt{5}}{2}\right\}$.

b) ${\left(x^2-4x+2\right)}^2+x^2-4x-4=0$

$\iff$ ${\left(x^2-4x+2\right)}^2+x^2-4x+2-6=0$

Đặt $x^2-4x+2=t$ khi đó phương trình trở thành 

t² + t – 6 = 0 (2)

Ta có a = 1; b = 1; c = -6

⇒ Δ = 1² – 4.1.(-6) = 25 > 0

⇒ (2) có hai nghiệm phân biệt

$t_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-1+\sqrt{25}}{2}=2$

$t_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-1-\sqrt{25}}{2}=-3$

+ Với t = 2 ⇒ x² – 4x + 2 = 2

⇔ x² – 4x = 0

⇔ x(x – 4) = 0

⇔ x = 0 hoặc x = 4.

+ Với t = -3 ⇒ x² – 4x + 2 = -3

⇔ x² – 4x + 5 = 0 (*)

Có a = 1; b = -4; c = 5 ⇒ Δ’ = (-2)² – 1.5 = -1 < 0

⇒ (*) vô nghiệm.

Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.

c) Điều kiện: $x\ge 0$

$x-\sqrt{x}=5\sqrt{x}+7$ (1)

Đặt $\sqrt{x}=t$ $\left(t\ge 0\right)$. Khi đó phương trình (1) trở thành:

$t^2-t=5t+7$(2)

Giải (2): Có a = 1; b = -6; c = -7

⇒ a – b + c = 0

⇒ (2) có nghiệm t₁ = -1; t₂ = $\frac{-c}{a}=\frac{7}{1}$ = 7.

Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.

+ Với t = 7 ⇒ $\sqrt{x}$ = 7 ⇔ x = 49 (thỏa mãn).

Vậy phương trình đã cho có tập nghiệm $S=\left\{49\right\}$

d) Điều kiện: $x\ne 0;x\ne -1$

$\frac{x}{x+1}-10.\frac{x+1}{x}=3$ (1)

Đặt $\frac{x}{x+1}=t$ khi đó phương trình (1) trở thành:

t - $10.\frac{1}{t}=3$

$\Rightarrow t^2-10=3t$

$\iff t^2-3t-10=0$(2)

Ta có: a = 1; b = -3; c = -10.

$\Delta ={\left(-3\right)}^2-\mathrm{4.1.}\left(-10\right)=9+40=49>0$

Phương trình (2) có hai nghiệm phân biệt

$t_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{3+\sqrt{49}}{2.1}=5$;

$t_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{3-\sqrt{49}}{2.1}=-2$.

+) Với t = 5 $\Rightarrow \frac{x}{x+1}=5$

$\iff x=5\left(x+1\right)$

$\iff x=5x+5$

$\iff 5x-x=-5$

$\iff 4x=-5$

$\iff x=\frac{-5}{4}$ (thỏa mãn)

+) Với t = -2 $\Rightarrow \frac{x}{x+1}=-2$

$\iff x=-2\left(x+1\right)$

$\iff x=-2x-2$

$\iff x+2x=-2$

$\iff 3x=-2$

$\iff x=\frac{-2}{3}$ (thỏa mãn)

Vậy phương trình đã cho có tập nghiệm S = $\left\{\frac{-5}{4};\frac{-2}{3}\right\}$

Bài 7: Giải phương trình bằng cách đưa về phương trình tích:

a) $\left(3x^2-7x-10\right)$ $\left[2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3\right]=0$

b) $x^3+3x^2-2x-6=0$

c) $\left(x^2-1\right)\left(0,6x+1\right)=0,6x^2+x$

d) ${\left(x^2+2x-5\right)}^2={\left(x^2-x+5\right)}^2$

Lời giải

a) $\left(3x^2-7x-10\right)$$\left[2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3\right]=0$

$\iff \left[\begin{array}{l}3x^2-7x-10=0\text{ (1)}\\ 2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3=0\text{ (2)}\end{array}\right.$

+) Giải (1): $3x^2-7x-10=0$

Ta có: a = 3; b = -7; c = -10

Nhận thấy a – b + c = 0

Do đó phương trình (1) có nghiệm $x_1=-1;x_2=\frac{-c}{a}=\frac{10}{3}$

+) Giải (2): $2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3=0$

Ta có: a = 2; b = $1-\sqrt{5}$; c = $\sqrt{5}-3$

Nhận thấy a + b + c = 0 

Do đó phương trình (2) có nghiệm $x_1=1;x_2=\frac{c}{a}=\frac{\sqrt{5}-3}{2}$

Vậy phương trình có tập nghiệm là S = $\left\{-1;\frac{\sqrt{5}-3}{2};1;\frac{10}{3}\right\}$.

b) $x^3+3x^2-2x-6=0$

$\iff x^2\left(x+3\right)-2\left(x+3\right)=0$

$\iff \left(x+3\right)\left(x^2-2\right)=0$

$\iff \left(x+3\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0$

$\iff \left[\begin{array}{l}x+3=0\\ x-\sqrt{2}=0\\ x+\sqrt{2}=0\end{array}\right.$ $\iff \left[\begin{array}{l}x=-3\\ x=\sqrt{2}\\ x=-\sqrt{2}\end{array}\right.$

Vậy phương trình có tập nghiệm là S = $\left\{-3;-\sqrt{2};\sqrt{2}\right\}$ .

c) $\left(x^2-1\right)\left(0,6x+1\right)=0,6x^2+x$

$\iff \left(x^2-1\right)\left(0,6x+1\right)=x\left(0,6x+1\right)$

$\iff \left(x^2-1\right)\left(0,6x+1\right)-x\left(0,6x+1\right)=0$

$\iff \left(0,6x+1\right)\left(x^2-1-x\right)=0$

$\iff \left[\begin{array}{l}0,6x+1=0\text{ (1)}\\ x^2-x-1=0\text{ (2)}\end{array}\right.$

+) Giải (1): 0,6x + 1 = 0

$\iff 0,6x=-1$

$\iff x=(-1):0,6=\frac{-5}{3}$

Phương trình (1) có nghiệm x = $\frac{-5}{3}$

+) Giải (2): $x^2-x-1=0$

Ta có: a = 1; b = -1; c = -1

$\Delta ={\left(-1\right)}^2-\mathrm{4.1.}\left(-1\right)=1+4=5>0$

Phương trình hai có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{1+\sqrt{5}}{2}$ ;

$x_1=\frac{-b-\sqrt{\Delta }}{2a}=\frac{1-\sqrt{5}}{2}$

Vậy tập nghiệm của phương trình là S = $\left\{\frac{-5}{3};\frac{1-\sqrt{5}}{2};\frac{1+\sqrt{5}}{2}\right\}$ .

d) ${\left(x^2+2x-5\right)}^2={\left(x^2-x+5\right)}^2$

⇔ (x² + 2x – 5)² – (x² – x + 5)² = 0

⇔ [(x² + 2x – 5) – (x² – x + 5)].[(x² + 2x – 5) + (x² – x + 5)] = 0

$\iff \left(x^2+2x-5-x^2+x-5\right)\left(x^2+2x-5+x^2-x+5\right)=0$

⇔ (3x – 10)(2x² + x ) = 0

⇔ (3x – 10).x.(2x + 1) = 0

$\iff \left[\begin{array}{l}x=0\\ 3x-10=0\\ 2x+1=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ 3x=10\\ 2x=-1\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ x=\frac{10}{3}\\ x=\frac{-1}{2}\end{array}\right.$

Vậy phương trình có tập nghiệm $S=\left\{\frac{-1}{2};0;\frac{10}{3}\right\}$

Xem thêm các dạng bài tập toán hay khác:

50 Bài tập Giải bài toán bằng cách lập phương trình (có đáp án năm 2023)

50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)

50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)

50 Bài tập Giải bài toán bằng cách lập hệ phương trình (có đáp án năm 2023)

50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)