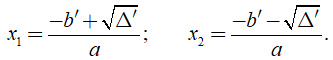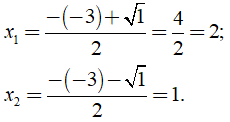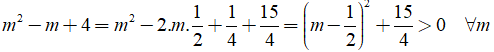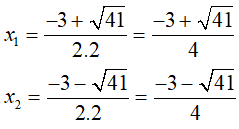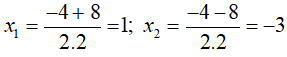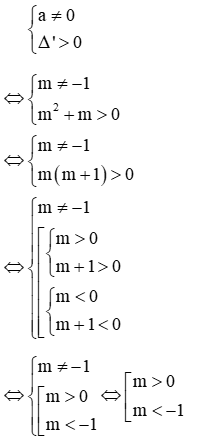Công thức nghiệm (2024) chi tiết nhất

Công Thức Nghiệm

1. Công thức nghiệm

Công thức nghiệm phương trình bậc 2

Đối với phương trình ax² + bx + c = 0 (a ≠ 0) và b = 2b'; Δ' = b'² - ac.

    + Nếu Δ' > 0, phương trình có hai nghiệm phân biệt

    + Nếu Δ' = 0, phương tình có nghiệm kép là x₁ = x₂ = -b'/a

    + Nếu Δ < 0, phương trình đã cho vô nghiệm.

2. Ví dụ minh họa

Câu 1: Giải phương trình 2x² - 6x + 4 = 0

Hướng dẫn:

    + Tính Δ' = (-3)² - 2.4 = 9 - 8 = 1 > 0

    + Do Δ' > 0, phương trình đã cho có hai nghiệm phân biệt là

Vậy phương trình đã cho có hai nghiệm là x₁ = 2; x₂ = 1.

Câu 2: Giải phương trình 3x² - 6x + 3 = 0

Hướng dẫn:

    + Tính Δ' = (-3)² - 3.3 = 9 - 9 = 0

    + Do Δ' = 0, phương trình có nghiệm kép là x₁ = x₂ = -(-3/3) = 1

Vậy phương trình có nghiệm kép là x₁ = x₂ = 1

Câu 3: Giải phương trình 5x² - 2x + 3 = 0

Hướng dẫn:

    + Tính Δ' = (-1)² - 5.3 = -14 < 0

    + Do Δ' < 0 nên phương trình đã cho vô nghiệm.

Vậy phương trình đã cho vô nghiệm.

3. Bài tập vận dụng

Câu 1: Tìm giá trị của tham số m để phương trình x² + 2mx + m - 4 = 0 có nghiệm.

Ta có: Δ' = m² - m + 4

Để phương trình có nghiệm thì Δ' ≥ 0 ⇔ m² - m + 4 ≥ 0

Mà 

Do đó Δ' > 0 ∀ m

⇔ Phương trình luôn có hai nghiệm phân biệt với mọi giá trị của m

Vậy với mọi giá trị của m thì phương trình đã cho có nghiệm.

Câu 2: Tìm giá trị của tham số m để phương trình x² - mx + m - 1 = 0 có đúng một nghiệm duy nhất?

Ta có:

Δ = (-m)² - 4m + 4 = m² - 4m + 4 = (m-2)²

Để phương trình đã cho có nghiệm duy nhất

⇔ Δ = 0 ⇔ (m-2)² = 0 ⇔ m = 2

Vậy với m = 2 thì phương trình đã cho có nghiệm duy nhất.

Câu 3: Giải các phương trình sau bằng công thức thu gọn:

3x² + 18x + 29 = 0;      x² - 16x + 64 = 0

Lời giải

Câu 4: Giải phương trình x² - 5x + 4 = 0

Lời giải

+ Tính Δ = (-5)² - 4.4.1 = 25 - 16 = 9 > 0

+ Do Δ > 0 , phương trình có hai nghiệm là:

 và 

Vậy phương trình có hai nghiệm là x₁ = 4; x₂ = 1

Câu 5: Giải phương trình 5x² - x + 2 = 0

Lời giải

+ Tính Δ = (-1)² - 4.5.2 = -39 < 0

+ Do Δ < 0, phương trình đã cho vô nghiệm

Vậy phương trình đã cho vô nghiệm

Câu 6 : Giải phương trình x² - 4x + 4 = 0.

Lời giải

+ Tính Δ = (-4)² - 4.4.1 = 16 - 16 = 0.

+ Do Δ = 0, phương trình có nghiệm kép là x₁ = x₂ =  = 2

Vậy phương trình có nghiệm kép là x = 2

Câu 7: Cho phương trình (m + 1)x² + 4x + 1 = 0. Tìm m để phương trình đã cho có nghiệm

A. m = -1

B. m = 0

C. m < 1

D. m ≤ 3

Lời giải:

* Với m = -1 thì phương trình đã cho trở thành: 4x + 1 = 0 ⇔ x = -1/4

Do đó, m = -1 thỏa mãn điều kiện.

* Nếu m ≠ -1 , khi đó phương trình đã cho là phương trình bậc hai một ẩn.

Ta có: Δ = 4² - 4.(m + 1).1 = 16 - 4m - 4 = 12 - 4m

Để phương trình đã cho có nghiệm khi: Δ = 12 - 4m ≥ 0

-4m ≥ - 12 ⇔ m ≤ 3

Kết hợp 2 trường hợp, để phương trình đã cho có nghiệm thì m ≤ 3 .

Chọn đáp án D.

Câu 8: Cho phương trình 2x² + 3x – 4 = 0 . Tìm mệnh đề sai trong các mệnh đề sau?

A. Phương trình đã cho có 2 nghiệm

B. Biệt thức ∆ = 41

C. Phương trình đã cho có nghiệm duy nhất

D. Phương trình đã cho có 2 nghiệm âm.

Lời giải:

Ta có: Δ = 3² - 4.2.(-4) = 9 + 32 = 41 > 0

Do đó, phương trình đã cho có 2 nghiệm phân biệt là:

Vậy C sai.

Chọn đáp án C.

Câu 9: Trong các phương trình sau, phương trình nào có nghiệm duy nhất.

A. x² - 4x+ 10 = 0

B. –2x² + 4x + 4 = 0

C. -3x² + 9 = 0

D. 4x² - 4x + 1 =0

Lời giải:

Ta tính ∆ của các phương trình đã cho:

A. ∆ = (-4)² - 4.1.10 = 16 – 40 = 24 > 0 nên phương trình này có hai nghiệm phân biệt

B. ∆ = 4² -4.(-2).4 = 16 + 32 = 48 > 0 nên phương trình này có hai nghiệm phân biệt.

C. ∆ = 0² – 4. (-2). 4 = 0 + 32 = 32 > 0 nên phương trình này có hai nghiệm phân biệt.

D. ∆ = (-4)² - 4.4.1 = 0 nên phương trình này có nghiệm duy nhất.

Chọn đáp án D.

Câu 10: Tìm giao điểm của đồ thị hàm số y = 2x² và đường thẳng y = - 4x + 6

A. A(1; 2) và B(- 3; 18)

B. A(1; 2) và B(3; -6)

C. A( 3; -6) và B( -1; 10)

D. Đáp án khác

Lời giải:

Hoành độ giao điểm của parabol và đường thẳng đã cho là nghiệm phương trình:

2x² = -4x + 6 2x² + 4x - 6 = 0 (*)

Phương trình này có Δ = 4² - 4.2.(-6) = 16 + 48 = 64

Do đó, phương trình (*) có hai nghiệm phân biệt:

Với x = 1 thì y = -4. 1 + 6 = 2 ta được điểm A(1; 2).

Với x = -3 thì y = -4.(-3) = 18 ta được điểm B( -3; 18)

Vậy parabol cắt đường thẳng tại hai điểm là A( 1;2) và B(- 3 ; 18)

Chọn đáp án A.

Câu 11: Cho phương trình (m + 1)x² – 2(m + 1)x + 1 = 0. Tìm các giá trị của m để phương trình có hai nghiệm phân biệt

A. m > 0     

B. m < −1   

C. −1 < m < 0       

D. Cả A và B đúng

Lời giải:

Phương trình (m + 1)x² – 2(m + 1)x + 1 = 0 có a = m + 1; b’ = − (m + 1); c = 1

Suy ra ∆' = [− (m + 1)]² – (m + 1) = m² + m

Để phương trình (m + 1)x² – 2(m + 1)x + 1 = 0 có hai nghiệm phân biệt thì:

Vậy m > 0 hoặc m < −1 thì phương trình có hai nghiệm phân biệt

Đáp án cần chọn là: D

Xem thêm các dạng bài tập Toán hay khác:

50 Bài tập Công thức nghiệm của phương trình bậc hai (có đáp án năm 2024)

50 Bài tập Công thức nghiệm thu gọn (có đáp án năm 2023)

30 Bài tập về Công thức nghiệm của phương trình bậc hai (2024)

500 Bài tập Toán 10 bất phương trình và hệ phương trình bậc nhất hai ẩn (có đáp án năm 2024)

40 Bài tập Phương trình quy về phương trình bậc nhất, bậc hai (2024)