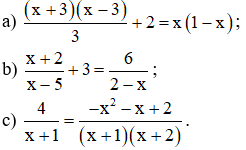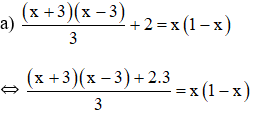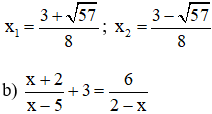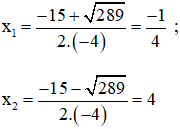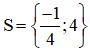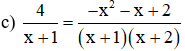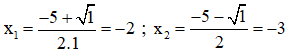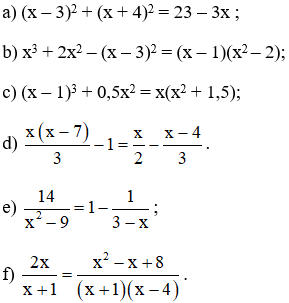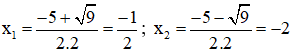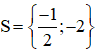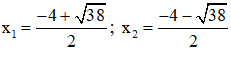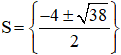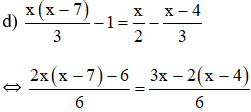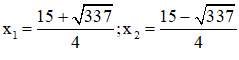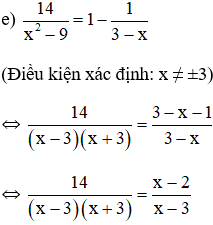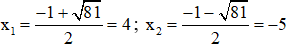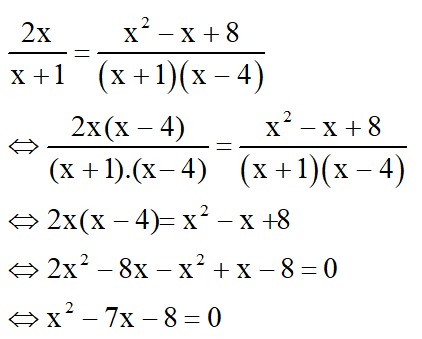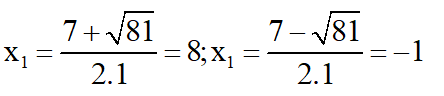50 Bài tập Phương trình quy về phương trình bậc hai (có đáp án năm 2024)

Bài tập Phương trình quy về phương trình bậc hai

Kiến thức cần nhớ 

1. Phương trình trùng phương

a) Phương trình trùng phương

Định nghĩa: Phương trình trùng phương là phương trình có dạng:

${\mathrm{ax}}^4+{\mathrm{bx}}^2+\mathrm{c}=0 \left(\mathrm{a}\ne 0\right)$(1)

Ví dụ 1: $3{\mathrm{x}}^4+3{\mathrm{x}}^2+6=0$; ${\mathrm{x}}^4-3{\mathrm{x}}^2=0$; ${\mathrm{x}}^4-16=0$… là những phương trình trùng phương.

Nhận xét: Phương trình trên không phải là phương trình bậc hai, song ta có thể đưa về phương trình bậc hai bằng cách đặt ẩn phụ

b) Các bước giải phương trình trùng phương

Bước 1: Đặt ẩn phụ

Đặt ${\mathrm{x}}^2=\mathrm{t}\left(\mathrm{t}\ge 0\right)$, khi đó phương trình (1) trở thành ${\mathrm{at}}^2+\mathrm{bt}+\mathrm{c}=0$(2)

Bước 2: Giải phương trình (2) với ẩn t

Bước 3: Giải phương trình t = x²

Bước 4: Trả lời

So sánh với điều kiện rồi kết luận nghiệm của phương trình.

2. Phương trình chứa ẩn ở mẫu

a) Phương trình chứa ẩn ở mẫu

Định nghĩa: Phương trình chứ ẩn ở mẫu là phương trình có chứa ẩn ở mẫu số.

Ví dụ 2: $\frac{2\mathrm{x}+3}{\mathrm{x}+5}+\frac{1}{\mathrm{x}-5}=0$; $\frac{4\mathrm{x}}{\mathrm{x}+3}-\frac{2\mathrm{x}-3}{\mathrm{x}+1}=6$… là những phương trình chứa ẩn ở mẫu.

b) Các bước giải phương trình chứa ân ở mẫu.

Bước 1: Tìm điều kiện xác định của phương trình.

Bước 2: Quy đồng mẫu thức hai vế rồi khử mẫu thức.

Bước 3: Giải phương trình vừa nhận được.

Bước 4: Trong các giá trị của ẩn vừa tìm được, loại các giá trị không thỏa mãn và kết luận nghiệm của phương trình.

3. Phương trình tích

a) Phương trình tích

Định nghĩa: Phương trình tích là phương trình có dạng A(x).B(x)….M(x) = 0, ở đó A(x); B(x); … M(x) là những biểu thức.

Ví dụ 3: $\left(\mathrm{x}+1\right)\left({\mathrm{x}}^2-6\mathrm{x}+5\right); {\left(\mathrm{x}+1\right)}^2\left(2{\mathrm{x}}^2+12\mathrm{x}+18\right)$ …

b) Các bước giải phương trình tích

Bước 1: Giải từng nhân tử A(x) = 0; B(x) = 0; …của phương trình

Bước 2: So sánh điều kiện kết luận tập nghiệm.

Bài tập vận dụng (có đáp án) 

Bài 1: Giải các phương trình:

Lời giải

⇔ (x + 3)(x – 3) + 2.3 = 3x(1 – x)

⇔ x² – 9 + 6 = 3x – 3x²

⇔ x² – 9 + 6 – 3x + 3x² = 0

⇔ 4x² – 3x – 3 = 0

Có a = 4; b = -3; c = -3 ⇒ Δ = (-3)² – 4.4.(-3) = 57 > 0

Phương trình có hai nghiệm

Điều kiện xác định: x ≠ 5; x ≠ 2.

Quy đồng và khử mẫu ta được :

(x + 2)(2 – x) + 3(2 – x)(x – 5) = 6(x – 5)

⇔ 4 – x² + 6x – 3x² – 30 + 15x = 6x – 30

⇔ 4 – x² + 6x – 3x² – 30 + 15x – 6x + 30 = 0

⇔ -4x² + 15x + 4 = 0

Có a = -4; b = 15; c = 4 ⇒ Δ = 15² – 4.(-4).4 = 289 > 0

Phương trình có hai nghiệm phân biệt:

Cả hai giá trị đều thỏa mãn điều kiện.

Vậy phương trình có tập nghiệm 

Điều kiện xác định: x ≠ -1; x ≠ -2.

Quy đồng và khử mẫu ta được:

4.(x + 2) = -x² – x + 2

⇔ 4x + 8 = -x² – x + 2

⇔ 4x + 8 + x² + x – 2 = 0

⇔ x² + 5x + 6 = 0.

Có a = 1; b = 5; c = 6 ⇒ Δ = 5² – 4.1.6 = 1 > 0

⇒ Phương trình có hai nghiệm phân biệt:

Chỉ có nghiệm x₂ = -3 thỏa mãn điều kiện xác định.

Vậy phương trình có nghiệm x = -3.

Bài 2: Giải các phương trình trùng phương:

a) x⁴ – 5x² + 4 = 0;

b) 2x⁴ – 3x² – 2 = 0;

c) 3x⁴ + 10x² + 3 = 0

Lời giải

a) x⁴ – 5x² + 4 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : t² – 5t + 4 = 0 (2)

Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm t₁ = 1; t₂ = $\frac{c}{a}=\frac{4}{1}$ = 4

Cả và thỏa mãn $t\ge 0$

+ Với t = 1 ⇒ x² = 1 ⇒ x = $\pm 1$

+ Với t = 4 ⇒ x² = 4 ⇒ x = $\pm 2$

Vậy phương trình đã cho có tập nghiệm $S=\left\{-2;-1;1;2\right\}$

b) 2x⁴ – 3x² – 2 = 0; (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : 2t² – 3t – 2 = 0 (2)

Giải (2) : Có a = 2 ; b = -3 ; c = -2

⇒ Δ = (-3)² - 4.2.(-2) = 25 > 0

⇒ Phương trình có hai nghiệm phân biệt

$t_1=\frac{3+\sqrt{25}}{2.2}=2;t_2=\frac{3-\sqrt{25}}{2.2}=\frac{-1}{2}$

Vì $t\ge 0$ nên chỉ có t = 2 thỏa mãn điều kiện

+ Với t = 2 ⇒ x² = 2 ⇒ x = $\pm \sqrt{2}$

Vậy phương trình đã cho có tập nghiệm $S=\left\{-\sqrt{2};\sqrt{2}\right\}$

c) 3x⁴ + 10x² + 3 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành: 3t² + 10t + 3 = 0 (2)

Giải (2) : Có a = 3; b' = 5; c = 3

⇒ Δ’ = 5² – 3.3 = 16 > 0

⇒ Phương trình có hai nghiệm phân biệt

$t_1=\frac{-5+\sqrt{16}}{3}=\frac{-1}{3};t_2=\frac{-5-\sqrt{16}}{3}=-3$

Vì $t\ge 0$ nên cả đều $t_1;t_2$ không thỏa mãn.

Bài 3: Giải các phương trình:

a) (3x² – 5x + 1)(x² – 4) = 0;

b) (2x² + x – 4)² – (2x – 1)² = 0.

Lời giải

a) (3x² – 5x + 1)(x² – 4) = 0

$\left[\begin{array}{l}3x^2-5x+1=0\text{ (1)}\\ x^2-4=0\text{ (2)}\end{array}\right.$

+ Giải (1): 3x² – 5x + 1 = 0

Có a = 3; b = -5; c = 1 ⇒ Δ = (-5)² – 4.3 = 13 > 0

Phương trình có hai nghiệm phân biệt

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{5+\sqrt{13}}{2.3}=\frac{5+\sqrt{13}}{6}$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{5-\sqrt{13}}{2.3}=\frac{5-\sqrt{13}}{6}$

+ Giải (2): x² – 4 = 0 ⇔ x² = 4 ⇔ x = $\pm$2

Vậy phương trình ban đầu có tập nghiệm $S=\left\{-2;\frac{5-\sqrt{13}}{6};2;\frac{5+\sqrt{13}}{6}\right\}$

b) (2x² + x – 4)² – (2x – 1)² = 0

⇔ (2x² + x – 4 – 2x + 1)(2x² + x – 4 + 2x – 1) = 0

⇔ (2x² – x – 3)(2x² + 3x – 5) = 0

⇔ 2x² – x – 3 = 0 (1)

hoặc 2x² + 3x – 5 = 0 (2)

+ Giải (1): 2x² – x – 3 = 0

Có a = 2; b = -1; c = -3 ⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm x = -1 và x = -$\frac{c}{a}$ = $\frac{3}{2}$.

+ Giải (2): 2x² + 3x – 5 = 0

Có a = 2; b = 3; c = -5 ⇒ a + b + c = 0

⇒ Phương trình có hai nghiệm x = 1 và x = $\frac{c}{a}$ = -$\frac{5}{2}$.

Vậy phương trình có tập nghiệm S = $\left\{\frac{-5}{2};-1;1;\frac{3}{2}\right\}$

Bài 4: Giải phương trình trùng phương:

a)$9x^4-10x^2+1=0$

b)$5x^4+2x^2-16=10-x^2$

c)$0,3x^4+1,8x^2+1,5=0$

d)$2x^2+1=\frac{1}{x^2}-4$

Lời giải

a) 9x⁴ – 10x² + 1 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : 9t² – 10t + 1 = 0 (2)

Giải (2):

Có a = 9; b = -10; c = 1

⇒ a + b + c = 0

⇒ Phương trình (2) có nghiệm t₁ = 1; t₂ = $\frac{c}{a}=\frac{1}{9}$

Cả hai nghiệm đều thỏa mãn điều kiện.

+ Với t = 1 ⇒ x² = 1 ⇒ x = $\pm 1$

+ Với t = $\frac{1}{9}\Rightarrow x=\pm \sqrt{\frac{1}{9}}=\pm \frac{1}{3}$.

Vậy phương trình có tập nghiệm $S=\left\{-1;\frac{-1}{3};\frac{1}{3};1\right\}$

b) 5x⁴ + 2x² – 16 = 10 – x²

⇔ 5x⁴ + 2x² – 16 – 10 + x² = 0

⇔ 5x⁴ + 3x² – 26 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó (1) trở thành : 5t² + 3t – 26 = 0 (2)

Giải (2) :

Có a = 5 ; b = 3 ; c = -26

⇒ Δ = 3² – 4.5.(-26) = 529 > 0

⇒ Phương trình có hai nghiệm phân biệt:

$t_1=\frac{-3+\sqrt{529}}{2.5}=2;t_2=\frac{-3-\sqrt{529}}{2.5}=\frac{-26}{10}$

Đối chiếu điều kiện $t\ge 0$ chỉ có t₁ = 2 thỏa mãn

+ Với t = 2 ⇒ x² = 2 ⇒ x = $\pm \sqrt{2}$

Vậy phương trình (1) có tập nghiệm S = $\left\{-\sqrt{2};\sqrt{2}\right\}$

c) 0,3x⁴ + 1,8x² + 1,5 = 0 (1)

Đặt x² = t, điều kiện t ≥ 0.

Khi đó, (1) trở thành : 0,3t² + 1,8t + 1,5 = 0 (2)

Giải (2) :

Ta có: a = 0,3 ; b = 1,8 ; c = 1,5

⇒ a – b + c = 0

⇒ Phương trình có hai nghiệm t₁ = -1 và t₂ = $\frac{-c}{a}=\frac{-1,5}{0,3}=-5$

Cả hai nghiệm đều không thỏa mãn điều kiện $t\ge 0$.

Vậy phương trình (1) vô nghiệm.

d) Điều kiện xác định: x ≠ 0.

$2x^2+1=\frac{1}{x^2}-4$

$\iff \frac{2x^4}{x^2}+\frac{x^2}{x^2}=\frac{1}{x^2}-\frac{4x^2}{x^2}$

2x⁴ + x² = 1 – 4x²

⇔ 2x⁴ + x² + 4x² – 1 = 0

⇔ 2x⁴ + 5x² – 1 = 0 (1)

Đặt t = x², điều kiện t > 0.

Khi đó (1) trở thành : 2t² + 5t – 1 = 0 (2)

Giải (2) :

Có a = 2 ; b = 5 ; c = -1

⇒ Δ = 5² – 4.2.(-1) = 33 > 0

⇒ Phương trình có hai nghiệm phân biệt:

$t_1=\frac{-5+\sqrt{33}}{4};t_2=\frac{-5-\sqrt{33}}{4}$

Đối chiếu với điều kiện t > 0 thấy có nghiệm t₁ thỏa mãn.

+ Với t = $\frac{-5+\sqrt{33}}{4}\Rightarrow x^2=\frac{-5+\sqrt{33}}{4}$

$\Rightarrow x=\pm \sqrt{\frac{-5+\sqrt{33}}{4}}=\pm \frac{\sqrt{-5+\sqrt{33}}}{2}$ (thỏa mãn)

Vậy phương trình có tập nghiệm S = $\left\{\pm \frac{\sqrt{-5+\sqrt{33}}}{2}\right\}$

Bài 5: Giải các phương trình:

Lời giải

a) (x – 3)² + (x + 4)² = 23 – 3x

⇔ x² – 6x + 9 + x² + 8x + 16 = 23 – 3x

⇔ x² – 6x + 9 + x² + 8x + 16 + 3x – 23 = 0

⇔ 2x² + 5x + 2 = 0

Có a = 2; b = 5; c = 2 ⇒ Δ = 5² – 4.2.2 = 9 > 0

⇒ Phương trình có hai nghiệm:

Vậy phương trình có tập nghiệm 

b) x³ + 2x² – (x – 3)² = (x – 1)(x² – 2)

⇔ x³ + 2x² – (x² – 6x + 9) = x³ – x² – 2x + 2

⇔ x³ + 2x² – x² + 6x – 9 – x³ + x² + 2x – 2 = 0

⇔ 2x² + 8x – 11 = 0.

Có a = 2; b = 8; c = -11 ⇒ Δ’ = 4² – 2.(-11) = 38 > 0

⇒ Phương trình có hai nghiệm:

Vậy phương trình có tập nghiệm 

c) (x – 1)³ + 0,5x² = x(x² + 1,5)

⇔ x³ - 3x² + 3x – 1 + 0,5x² = x³ + 1,5x

⇔ x³ + 1,5x – x³ + 3x² – 3x + 1 – 0,5x² = 0

⇔ 2,5x² – 1,5x + 1 = 0

Có a = 2,5; b = -1,5; c = 1

⇒ Δ = (-1,5)² – 4.2,5.1 = -7,75 < 0

Vậy phương trình vô nghiệm.

⇔ 2x(x – 7) – 6 = 3x – 2(x – 4)

⇔ 2x² – 14x – 6 = 3x – 2x + 8

⇔ 2x² – 14x – 6 – 3x + 2x – 8 = 0

⇔ 2x² – 15x – 14 = 0.

Có a = 2; b = -15; c = -14

⇒ Δ = (-15)² – 4.2.(-14) = 337 > 0

⇒ Phương trình có hai nghiệm:

⇔ 14 = (x – 2)(x + 3)

⇔ 14 = x² – 2x + 3x – 6

⇔ x² + x – 20 = 0

Có a = 1; b = 1; c = -20

⇒ Δ = 1² – 4.1.(-20) = 81 > 0

Phương trình có hai nghiệm:

Cả hai nghiệm đều thỏa mãn điều kiện xác định.

Vậy phương trình có tập nghiệm S = {-5; 4}.

f) Điều kiện: x≠-1;x≠4

Ta có: a= 1, b = -7, c = - 8

∆ = (-7)² – 4.1. (- 8)= 81

=> Phương trình có hai nghiệm:

Kết hợp với diều kiện, nghiệm của phương trình đã cho là x = 8

Bài 6: Giải phương trình bằng cách đặt ẩn phụ:

a) $3{\left(x^2+x\right)}^2-2\left(x^2+x\right)-1=0$

b) ${\left(x^2-4x+2\right)}^2+x^2-4x-4=0$

c) $x-\sqrt{x}=5\sqrt{x}+7$

d) $\frac{x}{x+1}-10.\frac{x+1}{x}=3$

Hướng dẫn:

a) Đặt t = x² + x, ta có phương trình 3t² - 2t - 1 = 0. Giải phương trình này, ta tìm được hai giá trị của t. Thay mỗi giá trị của t vừa tìm được vào đẳng thức t = x² +x, ta được một phương trình của ẩn x. Giải mỗi phương trình này sẽ tìm được giá trị của x.

d) Đặt $\frac{x+1}{x}=t$ hoặc $\frac{x}{x+1}=t$

Lời giải

a) $3{\left(x^2+x\right)}^2-2\left(x^2+x\right)-1=0$

Đặt $x^2+x=t$ khi đó phương trình trở thành:

$3t^2-2t-1=0$

Ta có: a = 3; b = -2; c = -1

Nhận thấy a + b + c = 0

Phương trình có hai nghiệm phân biệt: 

$t_1=1;t_2=\frac{c}{a}=\frac{-1}{3}$

+) Với t = 1 $\Rightarrow x^2+x=1$

$\iff x^2+x-1=0$

Ta có: a = 1; b = 1; c = -1

$\Delta =b^2-4ac=1^2-\mathrm{4.1.}\left(-1\right)=5$

Phương trình có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-1+\sqrt{5}}{2};$

$x_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-1-\sqrt{5}}{2}$

+ Với t = $\frac{-1}{3}\Rightarrow x^2+x=\frac{-1}{3}$

$\iff x^2+x+\frac{1}{3}=0$

Ta có: a = 1; b = 1; c = $\frac{1}{3}$

$\Delta =1^2-\mathrm{4.1.}\frac{1}{3}=\frac{-1}{3}<0$$\Rightarrow$ vô nghiệm

Vậy phương trình đã cho có tập nghiệm $S=\left\{\frac{-1-\sqrt{5}}{2};\frac{-1+\sqrt{5}}{2}\right\}$.

b) ${\left(x^2-4x+2\right)}^2+x^2-4x-4=0$

$\iff$ ${\left(x^2-4x+2\right)}^2+x^2-4x+2-6=0$

Đặt $x^2-4x+2=t$ khi đó phương trình trở thành 

t² + t – 6 = 0 (2)

Ta có a = 1; b = 1; c = -6

⇒ Δ = 1² – 4.1.(-6) = 25 > 0

⇒ (2) có hai nghiệm phân biệt

$t_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{-1+\sqrt{25}}{2}=2$

$t_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{-1-\sqrt{25}}{2}=-3$

+ Với t = 2 ⇒ x² – 4x + 2 = 2

⇔ x² – 4x = 0

⇔ x(x – 4) = 0

⇔ x = 0 hoặc x = 4.

+ Với t = -3 ⇒ x² – 4x + 2 = -3

⇔ x² – 4x + 5 = 0 (*)

Có a = 1; b = -4; c = 5 ⇒ Δ’ = (-2)² – 1.5 = -1 < 0

⇒ (*) vô nghiệm.

Vậy phương trình ban đầu có tập nghiệm S = {0; 4}.

c) Điều kiện: $x\ge 0$

$x-\sqrt{x}=5\sqrt{x}+7$ (1)

Đặt $\sqrt{x}=t$ $\left(t\ge 0\right)$. Khi đó phương trình (1) trở thành:

$t^2-t=5t+7$(2)

Giải (2): Có a = 1; b = -6; c = -7

⇒ a – b + c = 0

⇒ (2) có nghiệm t₁ = -1; t₂ = $\frac{-c}{a}=\frac{7}{1}$ = 7.

Đối chiếu điều kiện chỉ có nghiệm t = 7 thỏa mãn.

+ Với t = 7 ⇒ $\sqrt{x}$ = 7 ⇔ x = 49 (thỏa mãn).

Vậy phương trình đã cho có tập nghiệm $S=\left\{49\right\}$

d) Điều kiện: $x\ne 0;x\ne -1$

$\frac{x}{x+1}-10.\frac{x+1}{x}=3$ (1)

Đặt $\frac{x}{x+1}=t$ khi đó phương trình (1) trở thành:

t - $10.\frac{1}{t}=3$

$\Rightarrow t^2-10=3t$

$\iff t^2-3t-10=0$(2)

Ta có: a = 1; b = -3; c = -10.

$\Delta ={\left(-3\right)}^2-\mathrm{4.1.}\left(-10\right)=9+40=49>0$

Phương trình (2) có hai nghiệm phân biệt

$t_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{3+\sqrt{49}}{2.1}=5$;

$t_2=\frac{-b-\sqrt{\Delta }}{2a}=\frac{3-\sqrt{49}}{2.1}=-2$.

+) Với t = 5 $\Rightarrow \frac{x}{x+1}=5$

$\iff x=5\left(x+1\right)$

$\iff x=5x+5$

$\iff 5x-x=-5$

$\iff 4x=-5$

$\iff x=\frac{-5}{4}$ (thỏa mãn)

+) Với t = -2 $\Rightarrow \frac{x}{x+1}=-2$

$\iff x=-2\left(x+1\right)$

$\iff x=-2x-2$

$\iff x+2x=-2$

$\iff 3x=-2$

$\iff x=\frac{-2}{3}$ (thỏa mãn)

Vậy phương trình đã cho có tập nghiệm S = $\left\{\frac{-5}{4};\frac{-2}{3}\right\}$

Bài 7: Giải phương trình bằng cách đưa về phương trình tích:

a) $\left(3x^2-7x-10\right)$ $\left[2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3\right]=0$

b) $x^3+3x^2-2x-6=0$

c) $\left(x^2-1\right)\left(0,6x+1\right)=0,6x^2+x$

d) ${\left(x^2+2x-5\right)}^2={\left(x^2-x+5\right)}^2$

Lời giải

a) $\left(3x^2-7x-10\right)$$\left[2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3\right]=0$

$\iff \left[\begin{array}{l}3x^2-7x-10=0\text{ (1)}\\ 2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3=0\text{ (2)}\end{array}\right.$

+) Giải (1): $3x^2-7x-10=0$

Ta có: a = 3; b = -7; c = -10

Nhận thấy a – b + c = 0

Do đó phương trình (1) có nghiệm $x_1=-1;x_2=\frac{-c}{a}=\frac{10}{3}$

+) Giải (2): $2x^2+\left(1-\sqrt{5}\right)x+\sqrt{5}-3=0$

Ta có: a = 2; b = $1-\sqrt{5}$; c = $\sqrt{5}-3$

Nhận thấy a + b + c = 0 

Do đó phương trình (2) có nghiệm $x_1=1;x_2=\frac{c}{a}=\frac{\sqrt{5}-3}{2}$

Vậy phương trình có tập nghiệm là S = $\left\{-1;\frac{\sqrt{5}-3}{2};1;\frac{10}{3}\right\}$.

b) $x^3+3x^2-2x-6=0$

$\iff x^2\left(x+3\right)-2\left(x+3\right)=0$

$\iff \left(x+3\right)\left(x^2-2\right)=0$

$\iff \left(x+3\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0$

$\iff \left[\begin{array}{l}x+3=0\\ x-\sqrt{2}=0\\ x+\sqrt{2}=0\end{array}\right.$ $\iff \left[\begin{array}{l}x=-3\\ x=\sqrt{2}\\ x=-\sqrt{2}\end{array}\right.$

Vậy phương trình có tập nghiệm là S = $\left\{-3;-\sqrt{2};\sqrt{2}\right\}$ .

c) $\left(x^2-1\right)\left(0,6x+1\right)=0,6x^2+x$

$\iff \left(x^2-1\right)\left(0,6x+1\right)=x\left(0,6x+1\right)$

$\iff \left(x^2-1\right)\left(0,6x+1\right)-x\left(0,6x+1\right)=0$

$\iff \left(0,6x+1\right)\left(x^2-1-x\right)=0$

$\iff \left[\begin{array}{l}0,6x+1=0\text{ (1)}\\ x^2-x-1=0\text{ (2)}\end{array}\right.$

+) Giải (1): 0,6x + 1 = 0

$\iff 0,6x=-1$

$\iff x=(-1):0,6=\frac{-5}{3}$

Phương trình (1) có nghiệm x = $\frac{-5}{3}$

+) Giải (2): $x^2-x-1=0$

Ta có: a = 1; b = -1; c = -1

$\Delta ={\left(-1\right)}^2-\mathrm{4.1.}\left(-1\right)=1+4=5>0$

Phương trình hai có hai nghiệm phân biệt:

$x_1=\frac{-b+\sqrt{\Delta }}{2a}=\frac{1+\sqrt{5}}{2}$ ;

$x_1=\frac{-b-\sqrt{\Delta }}{2a}=\frac{1-\sqrt{5}}{2}$

Vậy tập nghiệm của phương trình là S = $\left\{\frac{-5}{3};\frac{1-\sqrt{5}}{2};\frac{1+\sqrt{5}}{2}\right\}$ .

d) ${\left(x^2+2x-5\right)}^2={\left(x^2-x+5\right)}^2$

⇔ (x² + 2x – 5)² – (x² – x + 5)² = 0

⇔ [(x² + 2x – 5) – (x² – x + 5)].[(x² + 2x – 5) + (x² – x + 5)] = 0

$\iff \left(x^2+2x-5-x^2+x-5\right)\left(x^2+2x-5+x^2-x+5\right)=0$

⇔ (3x – 10)(2x² + x ) = 0

⇔ (3x – 10).x.(2x + 1) = 0

$\iff \left[\begin{array}{l}x=0\\ 3x-10=0\\ 2x+1=0\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ 3x=10\\ 2x=-1\end{array}\right.$

$\iff \left[\begin{array}{l}x=0\\ x=\frac{10}{3}\\ x=\frac{-1}{2}\end{array}\right.$

Vậy phương trình có tập nghiệm $S=\left\{\frac{-1}{2};0;\frac{10}{3}\right\}$

Xem thêm các dạng bài tập toán hay khác:

50 Bài tập Giải bài toán bằng cách lập phương trình (có đáp án năm 2023)

50 Bài tập Hệ thức Vi – ét và ứng dụng (có đáp án năm 2023)

50 Bài tập Phương trình bậc hai một ẩn (có đáp án năm 2023)

50 Bài tập Giải bài toán bằng cách lập hệ phương trình (có đáp án năm 2023)

50 Bài tập Giải hệ phương trình bằng phương pháp cộng đại số (có đáp án năm 2023)