Bài toán xác định min max của hàm số trên đoạn
I. Kiến thức cần nhớ
1. Giá trị lớn nhất
Định nghĩa:
Số gọi là giá trị lớn nhất (GTLN) của hàm số trên D nếu
Kí hiệu .
2. Giá trị nhỏ nhất
Định nghĩa:
Số gọi là giá trị nhỏ nhất (GTNN) của hàm số trên D nếu
Kí hiệu .
2. Cách tìm GTLN và GTNN của hàm số trên 1 đoạn.
Định lý 1: Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.
Quy tắc tìm giá trị lớn nhất , giá trị nhỏ nhất của hàm số liên tục trong 1 đoạn
Nhận xét. Nếu hàm số có đạo hàm giữ nguyên dấu trên đoạn thì hàm số đồng biến hoặc nghịch biến trên cả đoạn . Do đó, đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các đầu mút của đoạn.
Quy tắc: Để tìm GTLN, GTNN của hàm số liên tục trên ta làm như sau
B1: Tính và tìm các điểm mà tại đó hoặc hàm số không xác định.
B2: Tính các giá trị .
B3: Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Khi đó
;
* Hàm số liên tục trên 1 khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó.
II. Các dạng bài tập
Lý thuyết về giá trị lớn nhất, giá trị nhỏ nhất.
Tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số liên tục trên một đoạn.
Tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một khoảng.
Sử dụng GTLN, GTNN để giải phương trình, bất phương trình, hệ phương trình.
Sử dụng giá trị lớn nhất, giá trị nhỏ nhất để chứng minh bất đẳng thức.
Ứng dụng giá trị lớn nhất, giá trị nhỏ nhất của hàm số vào bài toán thực tế.
Một số ứng dụng sự biến thiên của hàm số.
BÀI TẬP MẪU
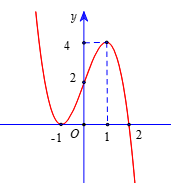
(ĐỀ MINH HỌA 2021) Cho hàm số , đồ thị của hàm số là đường cong trong hình bên. Giá trị lớn nhất của hàm số trên đoạn bằng
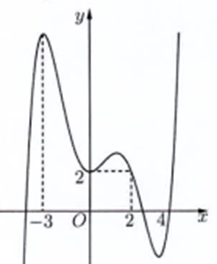
A. . B. . C. . D. .
Phân tích hướng dẫn giải
1. DẠNG TOÁN: Đây là dạng toán giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn.
2. HƯỚNG GIẢI:
Cách 1.
B1: Đạo hàm – tìm nghiệm của đạo hàm (đặt ẩn phụ nếu cần)
B2: Lập bảng biến thiên tìm ra giá trị lớn nhất – nhỏ nhất
Cách 2.
Dùng định nghĩa
thì
thì
Từ đó, ta có thể giải bài toán cụ thể như sau:
Lời giải
Chọn C
Ta có: .
Ta có bảng biến thiên của hàm số :
Từ bảng biến thiên ta có: trên hàm số đạt giá trị lớn nhất tại và .
BÀI TẬP TƯƠNG TỰ
Câu 1. Cho hàm số có đồ thị như hình vẽ
Giá trị nhỏ nhất của hàm số trên đoạn bằng
A.. B. . C. . D. .
Lời giải
Chọn D
Ta có
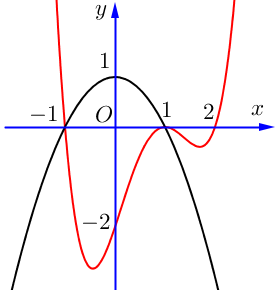
Bảng biến thiên
Từ BBT ta thấy .
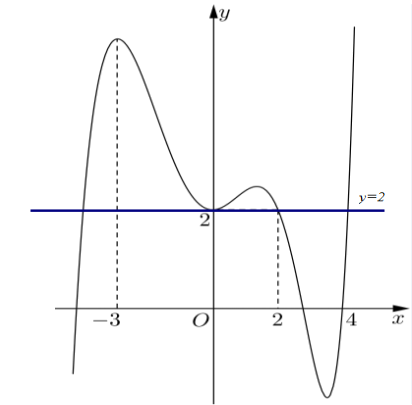
Câu 2. Cho hàm số có đồ thị hàm số như hình vẽ
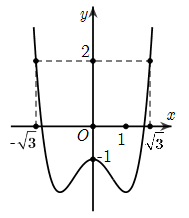
Đặt . Gọi , lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn . Hãy tính
A. . B. .
C. . D. .
Lời giải
Chọn D
Xét , với .
Ta có .
.
Bảng biến thiên của hàm số
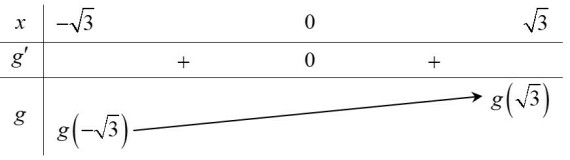
Do đó
,
.
Vậy
Câu 3. Cho hàm số . Biết hàm số có đồ thị như hình bên. Trên đoạn ,hàm sốđạt giá trị nhỏ nhất tại điểm.
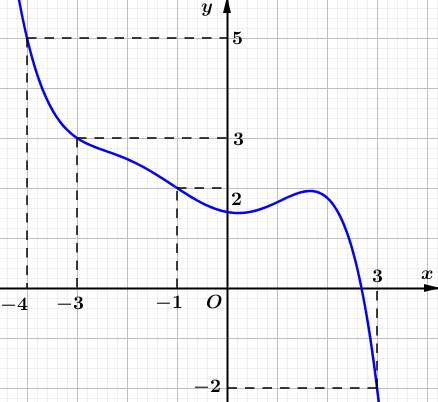
A. . B. . C. . D. .
Lời giải
Chọn A
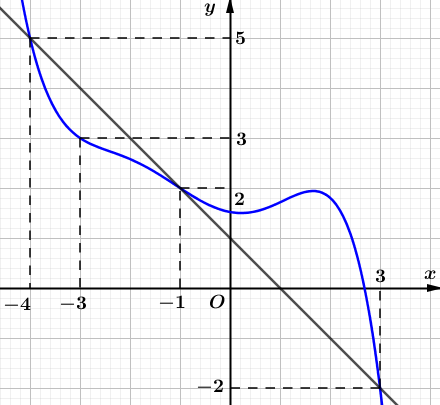
Ta có
.
Ta có bảng biến thiên:
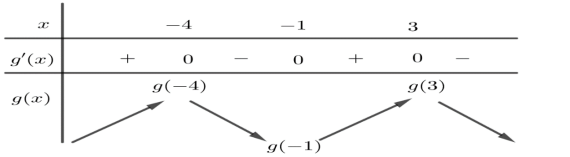
Từ bảng biến thiên, suy ra đạt giá trị nhỏ nhất trên đoạn tại
Ta có:
Vì trong đoạn đồ thị hàm số nằm phía dưới đồ thị hàm số
nghịch biến trên
Vì trong đoạn đồ thị hàm số nằm phía trên đồ thị hàm số
đồng biến trên
Từ và suy ra đạt giá trị nhỏ nhất trên đoạn tại
Câu 4. Cho hàm số liên tục trên . Đồ thị của hàm số như hình vẽ dưới đây.
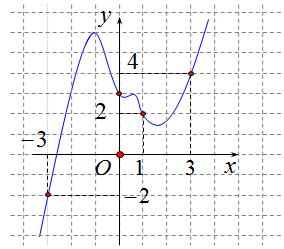
Xét hàm số . Mệnh đề nào sau đây là đúng?
A. . B. .
C. . D. Không tồn tại giá trị nhỏ nhất của hàm số trên .
Lời giải
Chọn B
.
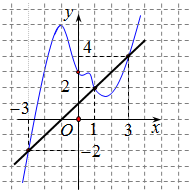
Dựa vào đồ thị hàm số ta thấy đường thẳng cắt đồ thị hàm số tại ba điểm lần lượt có hoành độ là: . Do đó phương trình .
Bảng biến thiên của hàm số
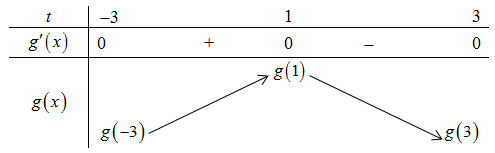
Vậy .
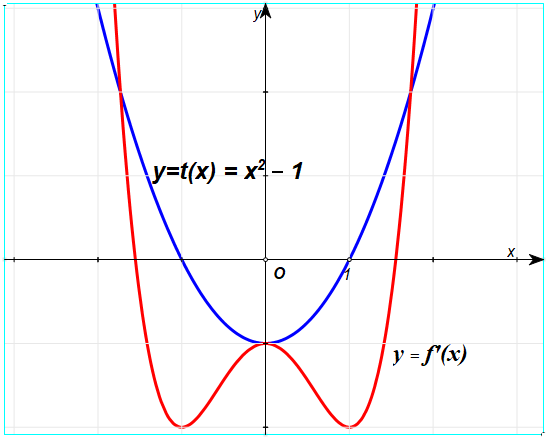
Câu 5. Cho hàm số liên tục trên và có đồ thị hàm số đạo hàm như hình vẽ.
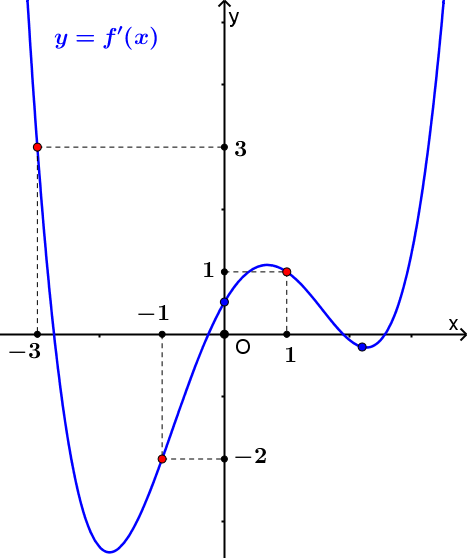
Xét hàm số . Mệnh đề nào dưới đây đúng?
A. . B. .
 C. . D. .
C. . D. .
Lời giải
Chọn C
Ta có: ;
.
Bảng biến thiên:
Dựa vào bảng biến thiên ta có: .
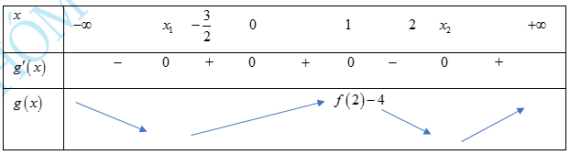
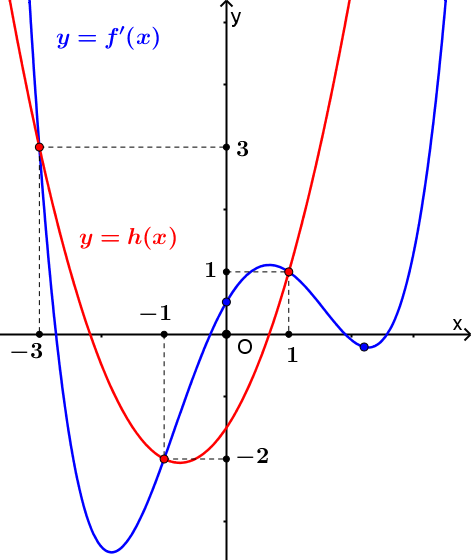
Câu 6. Cho hàm số có đạo hàm liên tục trên và có đồ thị hàm số như hình vẽ bên. Gọi . Biết .
Với thì đạt giá trị nhỏ nhất bằng
A. . B. . C. . D. .
Lời giải
Chọn A
+ Xét hàm số trên đoạn .
+ Ta có .
Vẽ đồ thị hàm số và Parabol trên cùng hệ trục tọa độ như hình vẽ.
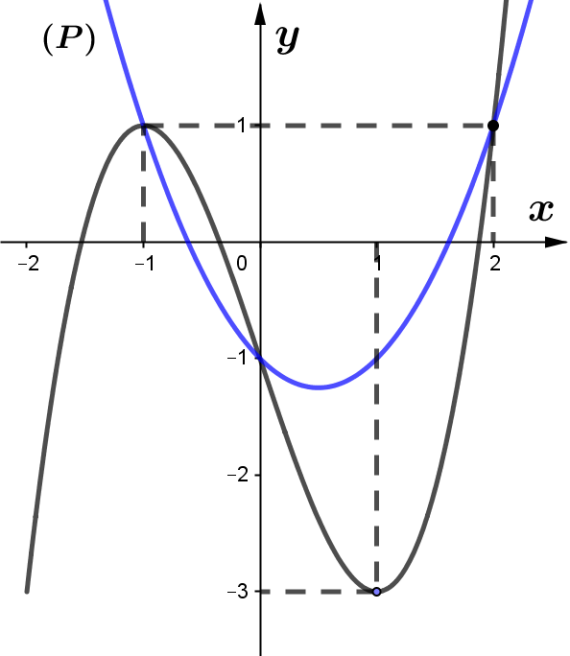
+ Ta thấy .
+ Bảng biến thiên :
+ Từ giả thiết
(vì )
.
Vậy .
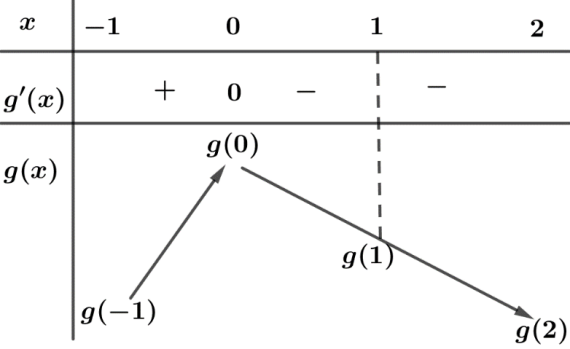
Câu 7. Cho hàm số có đạo hàm . Hàm số liên tục trên tập số thực và có đồ thị như hình vẽ.
Biết . Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên bằng
A. B. . C. . D. .
Lời giải
Chọn D
Từ đồ thị hàm số ta có bảng biến thiên
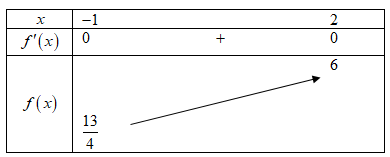
Ta có .
Xét trên đoạn ta có .
, .
Từ đó suy ra .
Vậy .
Câu 8. Cho hàm số có bảng biến thiên như hình dưới đây. Tìm giá trị lớn nhất của hàm số trên đoạn .
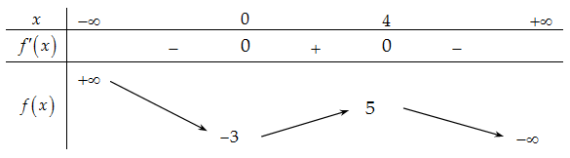
A. 15. B. . C. . D. 12.
Lời giải
Chọn D
.
Với thì ; nên .
Suy ra , .
Bảng biến thiên
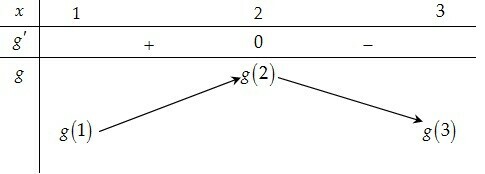
Suy ra .
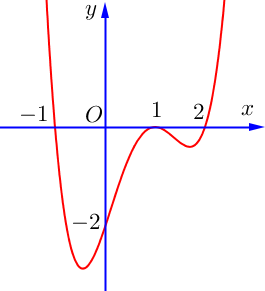
Câu 9. Cho hàm số có đạo hàm cấp 2 trên , hàm số có đồ thị như hình vẽ bên.
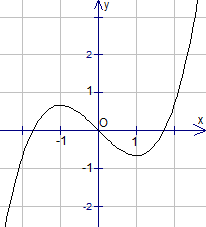
Giá trị lớn nhất của hàm số trên đoạn bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Đặt .
Vì .
Dựa vào đồ thị của hàm số , ta có bảng biến thiên
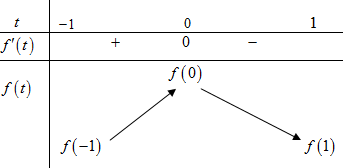
Ta có: .
Vậy .
Câu 10. Cho hàm số , hàm số có đồ thị như hình vẽ
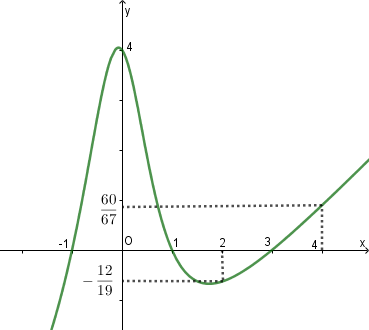
Giá trị nhỏ nhất của hàm số trên khoảng bằng
A. . B. .
C. . D. .
Lời giải
Chọn D
Ta có .
Đặt với .
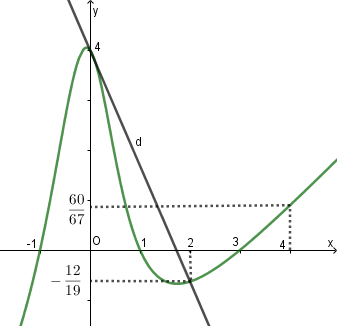
Từ đồ thị ta có .
Lập bảng biến thiên hàm số Giá trị nhỏ nhất hàm số đạt được khi .
suy ra .
Câu 11. Cho hàm số có đạo hàm liên tục trên và có đồ thị của hàm số trên đoạn như hình vẽ bên.
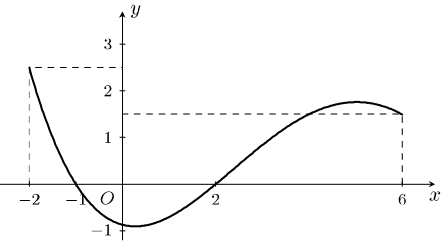
Tìm khẳng định đúng trong các khẳng định sau:
A. . B. .
C. . D. .
Lời giải
Chọn C
Lập bảng biến thiên của hàm số trên
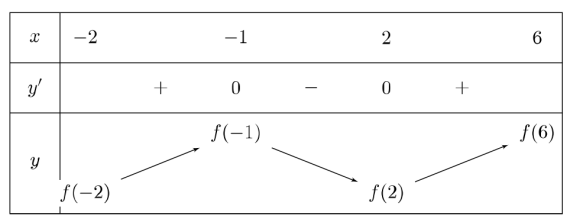
Dựa vào bảng biến thiên ta thấy:
Hàm số đồng biến trên và .
Suy ra và (1)
Hàm số nghịch biến trên suy ra .
Từ (1) và (2) suy ra :
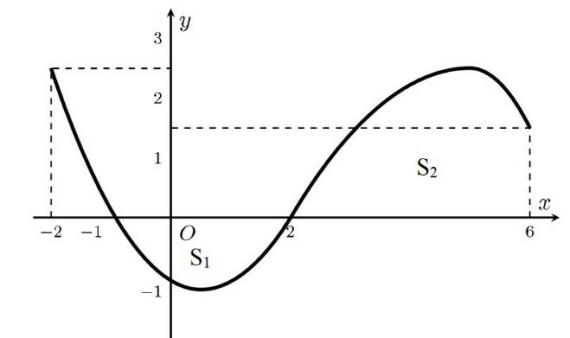
Ta có :
Theo hình vẽ ta thấy nên .
Vậy .
Câu 12. Cho hàm số liên tục trên và có bảng biến thiên trên đoạn như sau:
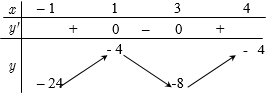
Giá trị lớn nhất của hàm số trên đoạn đoạn bằng
A. . B. . C. . D. .
Lời giải
Chọn B
Dựa vào bảng biến thiên, ta có ; .
Do đó, .
Câu 13. Cho hàm số liên tục trên và có đồ thị như hình vẽ bên dưới.
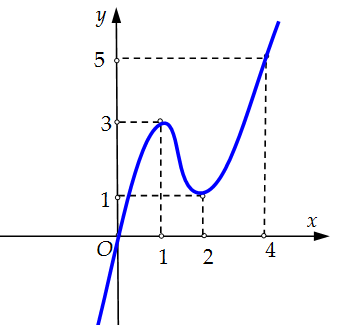
Gọi và lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên Giá trị của bằng
A. B. C. D.
Lời giải
Chọn A
Đặt Ta có:
Từ đồ thị ta thấy: .
Câu 14. Cho hàm số có bảng biến thiên như sau:
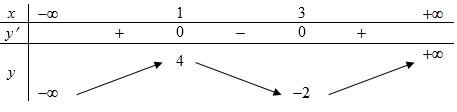
Tất cả các giá trị của để bất phương trình có nghiệm là
A. . B. . C. . D. .
Lời giải
Chọn B
Xét hàm số . Đặt
Khi đó: có nghiệm khi và chỉ khi có nghiệm
Từ bảng biến thiên ta thấy có nghiệm khi và chỉ khi
Câu 15. Cho hàm số . Hàm số có bảng biến thiên như sau:
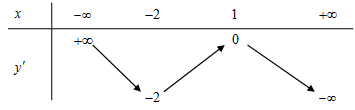
Bất phương trình đúng với mọi khi và chỉ khi
A. . B. . C. . D. .
Lời giải
Chọn C
.
Xét .
vì
Hàm số nghịch biến trên , .
đúng với mọi .
Câu 16. Cho hàm số liên tục trên và có đồ thị trên đoạn như hình vẽ bên dưới
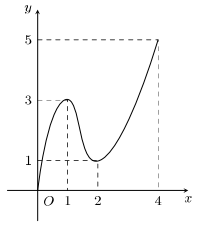
Đặt . Tổng bằng
A. . B. . C. . D. .
Lời giải
Chọn A
Đặt . Khi đó thì .
Xét hàm số trên đoạn ta thấy và .
Vậy .
Câu 17. Cho hàm số có đồ thị như hình bên. Tồn tại bao nhiêu giá trị nguyên của tham số để phương trình có đúng hai nghiệm thuộc đoạn
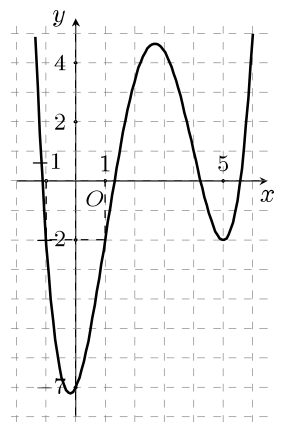
A. . B.. C.. D. .
Lời giải
Chọn C
Đăt để phương trình có đúng hai nghiệm thì phương trình có đúng môt nghiệm Dựa vào đồ thị ta có do nguyên nên Vậy có 5 giá trị.
Xem thêm các dạng bài tập hay, có đáp án:
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án
60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án - Toán 12
30 Bài tập Tính tích phân hàm số chẵn, hàm số lẻ (2024) cực hay, có đáp án




