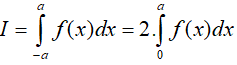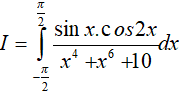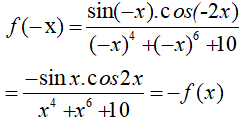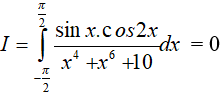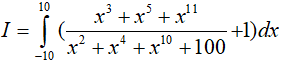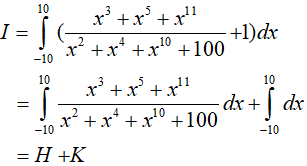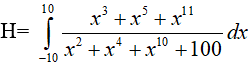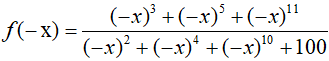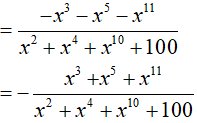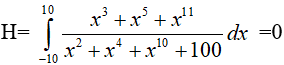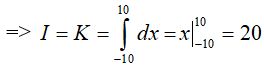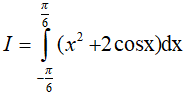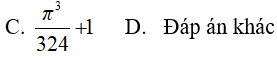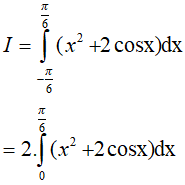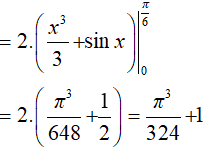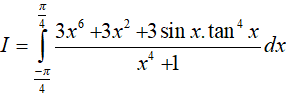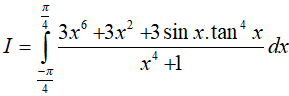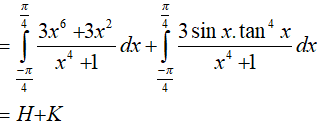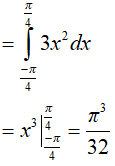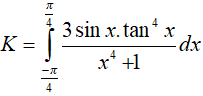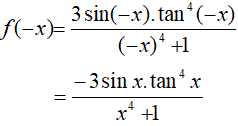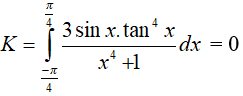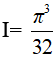Tích phân hàm số chẵn, hàm số lẻ
1. Phương pháp giải
Cho hàm số y= f(x) xác định, liên tục trên đoạn [−a; a].
• Nếu hàm số y= f (x) là hàm số chẵn thì 
• Nếu hàm số y= f(x) là hàm số lẻ thì 
2. Ví dụ minh họa
Ví dụ 1. Tính 
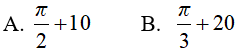
Lời giải:
Đáp án: D
Xét hàm số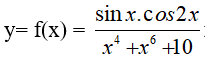 
xác định với mọi x.
Ta có:
Suy ra, hàm số y= f(x ) là hàm số lẻ nên ta có: 
Ví dụ 2. Tính 
A. 10 B. 20 C. 100 D. Đáp án khác
Lời giải:
Đáp án: B
Ta có;
+ Tính 
Xét hàm số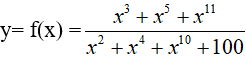 
xác định và liên tục trên [−10; 10].
Ta có:
Suy ra: f(−x) = −f(x) nên hàm số y = f(x) là hàm số lẻ.
Do đó: 
Ví dụ 4. Tính 
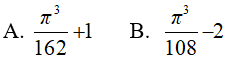
Lời giải:
Đáp án: C
Xét hàm số y = x2 + 2cosx xác định và liên tục trên R
Ta có; f(−x) = (−x)2 + 2. cos(−x) = x2 + 2cosx
Suy ra: f(x) = f(−x) nên hàm số f(x) là hàm số chẵn
Do đó, ta có;
Ví dụ 5. Tính 
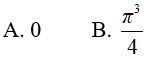
Lời giải:
Đáp án: D
Ta có:
Trong đó :
Và 
Xét hàm số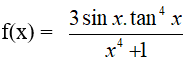 
liên tục trên R.
Ta có: 
Suy ra, f(−x) = −f(x) nên hàm số y = f(x) là hàm số lẻ.
Do đó, ta có: 
Vậy 
3. Bài tập vận dụng (có đáp án)
(Xem trong file đính kèm)
Xem thêm các dạng bài tập toán hay khác:
30 Bài tập Ứng dụng của tích phân tính diện tích hình phẳng (2024) cực hay
30 Bài tập Tính tích phân bằng phương pháp đổi biến số loại 1 (2024) cực hay, có đáp án
30 Bài tập Tính tích phân từng phần (2024) cực hay, có đáp án
20 Bài tập Tính tích phân hàm chứa dấu giá trị tuyệt đối (2024) chi tiết, có đáp án
20 Bài tập Tính tích phân bằng phương pháp đổi biến số loại 2 (2024) cực hay, có đáp án
