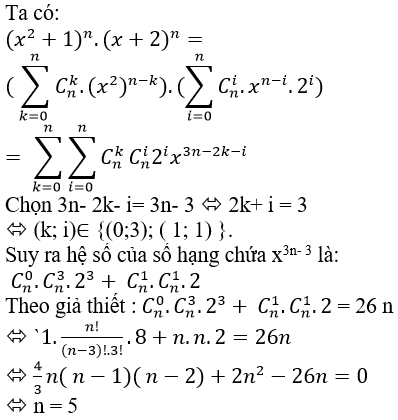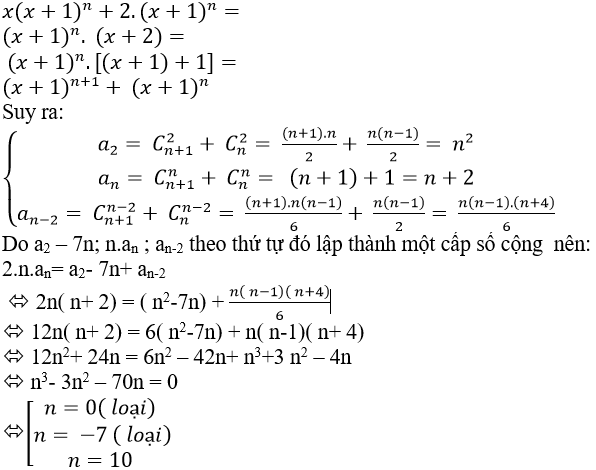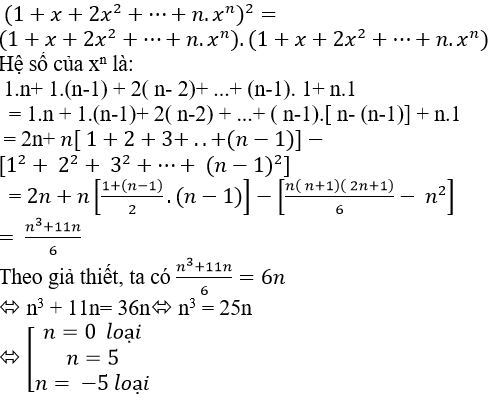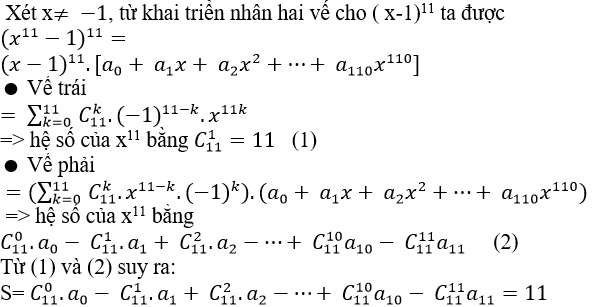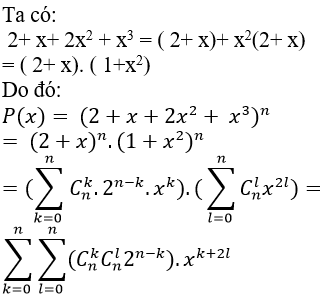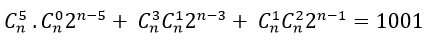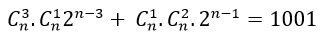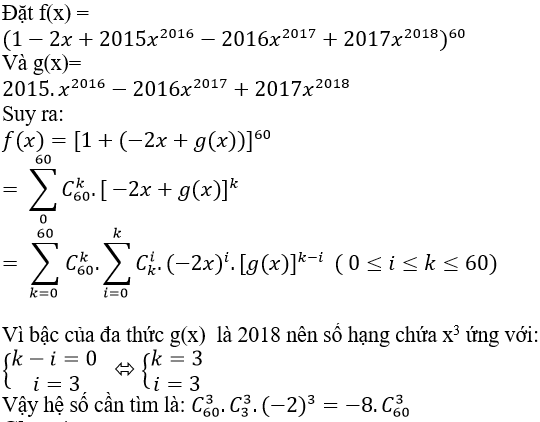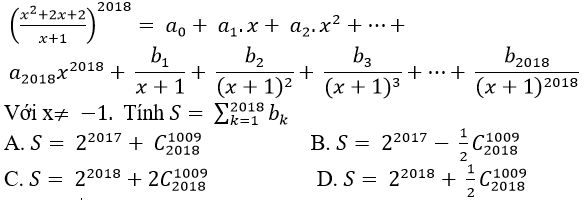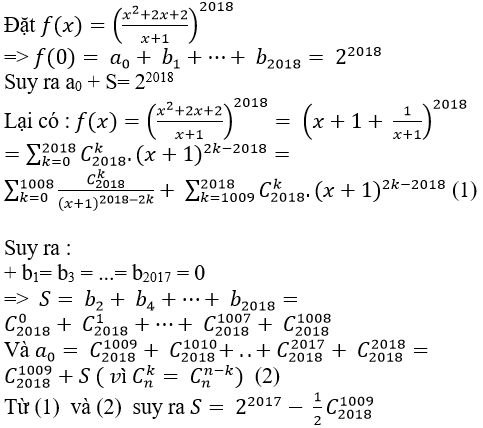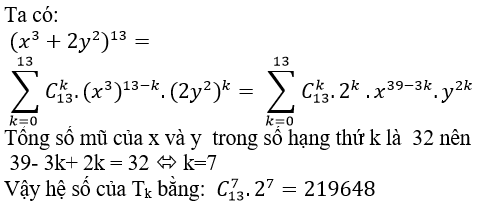Bài tập về bài vận dụng cao nhị thức newton
I. Lý thuyết Nhị thức Newton
1. Định nghĩa Nhị thức Newton
Nhị thức Newton là một định lý toán học quan trọng liên quan đến khai triển hàm mũ của tổng và phân tích các đa thức bậc cao. Định lý Nhị thức Newton có ứng dụng rộng rãi trong toán học và nhiều lĩnh vực khác, bao gồm:
+ Tính tổ hợp và chỉnh hợp: Định lý Nhị thức Newton là công cụ quan trọng trong việc tính toán số cách sắp xếp hoặc chọn k phần tử từ n phần tử mà không quan trọng thứ tự, điều này có ứng dụng trong nhiều vấn đề tổ hợp và chỉnh hợp.
+ Dãy số: Định lý Nhị thức Newton thường được sử dụng để chứng minh các thuộc tính của các dãy số, ví dụ như dãy số Fibonacci và dãy số Pascal.
+ Xác suất và thống kê: Trong xác suất và thống kê, định lý Nhị thức Newton được sử dụng để tính xác suất và biểu diễn các phân phối xác suất, nhất là trong việc tính toán xác suất của các biến ngẫu nhiên rời rạc.
+ Lý thuyết đồ thị: Công thức Nhị thức được sử dụng để tính toán số lượng đồ thị con trong một đồ thị, điều này có ứng dụng trong lý thuyết đồ thị và các vấn đề liên quan đến mạng lưới.
2. Công thức Nhị thức Newton
Với a,b là những số thực tùy ý và với mọi số tự nhiên n≥1, ta có:
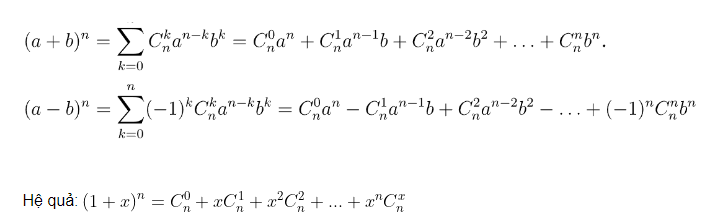
• (a+b)4=C04a4+C14a3b+C24a2b2+C34ab3+C44b4
=a4+4a3b+6a2b2+4ab3+b4;
• (a+b)5=C05a5+C15a4b+C25a3b2+C35a2b3+C45ab4+C55b5
=a5+5a4b+10a3b2+10a2b3+5ab4+b5.
Hai công thức trên gọi là công thức nhị thức Newton (gọi tắt là nhị thức Newton) (a+b)n ứng với n = 4 và n = 5.
Chú ý:
– Các hệ số trong khai triển nhị thức Newton (a + b)n với n = 0; 1; 2; 3; … được viết thành từng hàng và xếp thành bảng số như dưới đây.
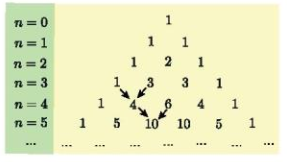
Bảng số này có quy luật: số đầu tiên và số cuối cùng của mỗi hàng đều là 1; tổng của 2 số liên tiếp cùng hàng bằng số của hàng kế dưới ở vị trí giữa hai số đó (được chỉ bởi mũi tên trên bảng).
Bảng số trên dược gọi là tam giác Pascal (đặt theo tên của nhà toán học, vật lí học, triết học người Pháp Blaise Pascal, 1623 – 1662).
II. Ví dụ minh họa
Ví dụ 1 : Sử dụng công thức nhị thức Newton khai triển biểu thức (a + 2)4.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
(a + 2)4 = 1.a4 + 4a3.2 + 6a2.22 + 4a.23 + 24
= a4 + 8a3 + 24a2 + 32a + 16.
Ví dụ 2: Khai triển và rút gọn biểu thức: (1+√5)5+(1−√5)5.
Hướng dẫn giải
Theo công thức nhị thức Newton ta có:
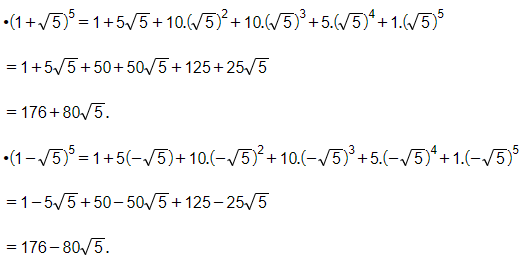
Do đó ta có: (1+√5)5+(1−√5)5=176+80√5+176−80√5=352.
III. Bài tập vận dụng
Câu 1: Gọi a3n- 3 là hệ số của số hạng chứa x3n- 3 trong khai triển (x2+1)n.(x+2)n. Tìm n sao cho a3n- 3 = 26n?
A.n=4 B.n=5 C.n=6 D.n=7
Lời giải:
Đáp án : B
Câu 2: Gọi a5n-10 là hệ số của số hạng chứa x5n-10 tronh khai triển (x3+1)n.(x2+2)n. Biết a5n- 10 = 1000n( n-1). Tìm n
A.n=13 B.n=15 C.n=16 D.n=17
Lời giải:
Đáp án : D
Ta có
Câu 3: Cho kahi triển x(x+1)n + 2( x+1)n= a0+ a1x+ a2.x2+ ...+ an+1xn+1 với n là số tự nhiên và n≥2. Tìm n; biết rằng a2 – 7n; n.an ; an-2 theo thứ tự đó lập thành một cấp số cộng.
A.n= 6 B.n= 8 C.n= 10 D.n= 12
Lời giải:
Đáp án : C
Ta có
Vậy n=10
Câu 4: Xác định n biết rằng hệ số của xn trong khai triển (1+x+2x2+⋯+n.xn )2 bằng 6n
A.n= 5 B.n= 6 C.n= 4 D.n= 7
Lời giải:
Đáp án : A
Ta có
Vậy n=10
Câu 5: Khai triển (1+x+ x2+ ..+ x10)11 được viết thành a0+ a1x+ a2.x2+ ...+a110x110.
A.S= 9 B.S= 10 C.S= 13 D.S= 11
Lời giải:
Đáp án : D
Câu 6: Biết rằng trong khai triển nhị thức Niu- tơn của đa thức P(x)= (2+x+ 2x2+ x3)n thì hệ số của x5 là 1001. Tổng các hệ số trong khai triển của P(x) bằng :
A.7776 B.6784 C.6842 D.8640
Lời giải:
Đáp án : A
Hệ số của x5 ứng với k+ 2l thỏa mãn : k+ 2l= 5
⇒ (k; l)= { (5; 0); (3,1); (1;2)}
Trường hợp 1. Với n≥5 khi đó (k; l)= { (5; 0); (3,1); (1;2)}
⇒ Hệ số của x5 là :
Vì vế trái lẻ mà vế phải luôn chẵn nếu n>5 do đó chỉ có thể chọn n=5.
Thử lại vào phương trình ta thấy thỏa mãn điều kiện.
Trường hợp 2. Với 3≤n<5 khi đó (k; l) = {(3;1); (1;2)}
⇒ Hệ số của x5 là :
Vì vế trái lẻ mà vế phải luôn chẵn nếu n>3 do đó chỉ có thể chọn n= 3
Thử lại vào phương trình ta thấy n= 3 không thỏa mãn điều kiện.
Trường hợp 3. Với n= 2 khi đó (k;l)= (1;2)
⇒ Hệ số của x5 là :
Do đó chỉ có n= 5 thỏa mãn nên tổng các hệ số trong khai triển:
Cho x= 1 ta được: 65 = 7776
Câu 7: Cho khai triển P(x)= (1+x).(2+ x). ..(1+2017x) = a0+ a1x+ a2x2+ ...+ a2017x2017. Kí hiệu P’(x) và P”(x) lần lượt là đạo hàm cấp 1 và đạo hàm cấp 2 của đa thức P(x). Khẳng định nào sau đây đúng?
A.a2 = P’(0) B.a2=(P'(0))/2 C.a2=P''(0) D.a2=(P^''(0))/2
Lời giải:
Đáp án : D
Ta có: P'(x)= a1+2a2x+3a3x2+⋯+2017a2017x2016
Tiếp tục đạo hàm lần nữa, ta có:
P''(x)=2a2+6a3x+⋯+2017.2016.a2017x2015
Cho x = 0 ta được: P''(0)=2a2 nên a2=(P^''(0))/2
Câu 8: Tìm hệ số của số hạng chứa x3 trong khai triển: (1-2x+2015x2016-2016x2017+2017.x2018)60
Lời giải:
Đáp án : A
Câu 9: Cho khai triển
Lời giải:
Đáp án : B
Câu 10: Gọi Tk là số hạng thứ k trong khai triển (x3+2y2)13 mà tổng số mũ của x và y trong số hạng đó bằng 32. Hệ số của Tk bằng?
A.198620 B.186284 C.219648 D.2012864
Hướng dẫn giải :
Đáp án : C
Câu 11: Cho khai triển: (x-1)2n+x.(x+1)(2n-1)= a0+ a1 x+ a2.x2+⋯+ a2n.x2n với n nguyên dương và n≥3. Biết rằng 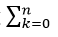
A.188 B.284 C.336 D.424
Hướng dẫn giải :
Đáp án : C
Đặt P(x)= (x-1)2n+x.(x+1)(2n-1)= a0+ a1 x+ a2.x2+⋯+ a2n.x2n
⇒ P(1)= 22n- 1 =a0+ a1 + ...+ a2n
Và P(-1)= 22n = a0- a1 + a2- ....+ a2n
⇒ P(1) + P(-1) = 22n-1 +22n = 2. 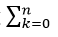
Suy ra: 22n-1 +22n = 1536 ⇔ n= 5
⇒hệ số a6 chứa x6 trong khai triển đã cho là:
Xem thêm các dạng câu hỏi và bài tập liên quan khác: