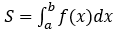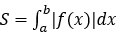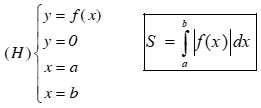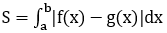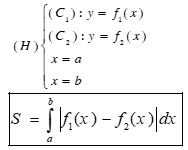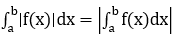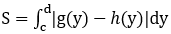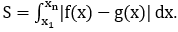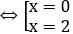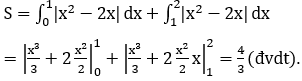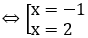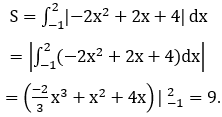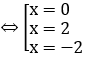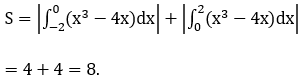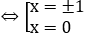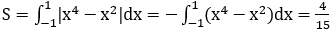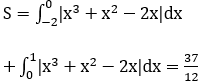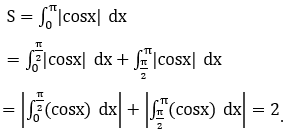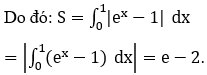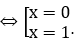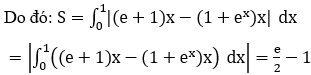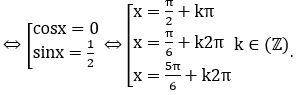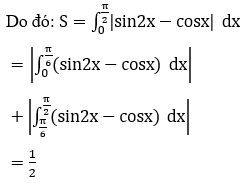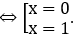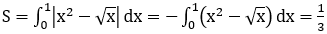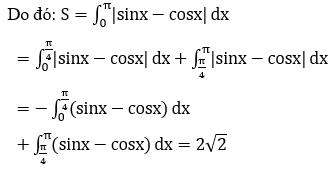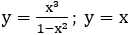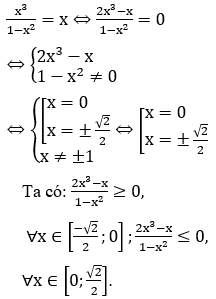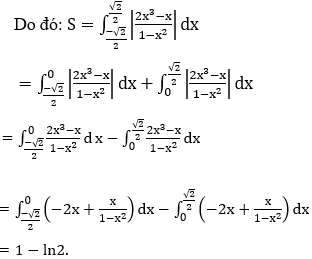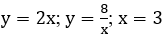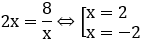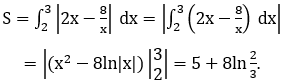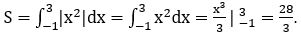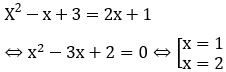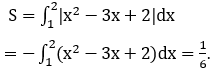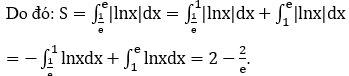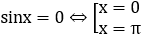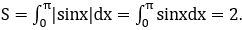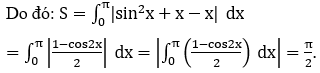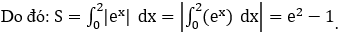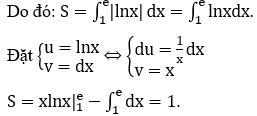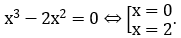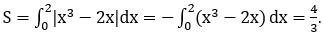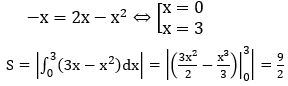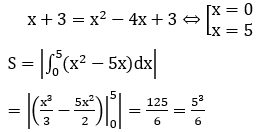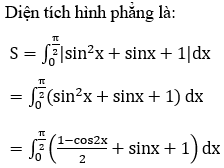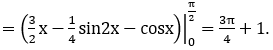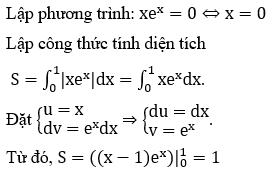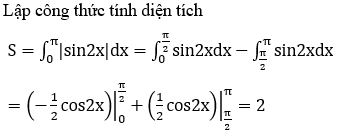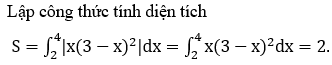30 Bài tập Ứng dụng của tích phân tính diện tích hình phẳng (2024) cực hay

Ứng dụng của tích phân Tính diện tích hình phẳng

1. Phương pháp giải

a. Định lý

Cho hàm số y=f(x) liên tục, không âm trên [a;b]. Khi đó diện tích S của hình thang cong giới hạn bởi đồ thị hàm số y=f(x), trục hoành và 2 đường thẳng x=a, x=b là:

b. Bài toán liên quan

    Bài toán 1: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x) liên tục trên đoạn [a;b], trục hoành và hai đường thẳng x=a, x=b được xác định:

    Bài toán 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=f(x), y=g(x) liên tục trên đoạn [a;b] và hai đường thẳng x=a, x=b được xác định:

    Chú ý:

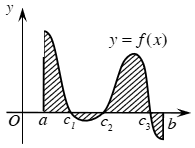
- Nếu trên đoạn [a;b], hàm số f(x) không đổi dấu thì:

- Nắm vững cách tính tích phân của hàm số có chứa giá trị tuyệt đối

    Bài toán 3: Diện tích của hình phẳng giới hạn bởi các đường x=g(y), x=h(y) và hai đường thẳng y=c, y=d được xác định:

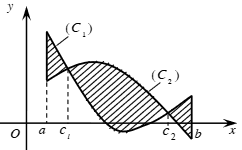
    Bài toán 4: Diện tích hình phẳng giới hạn bởi 2 đồ thị (C₁): f₁(x), (C₂):f₂(x) là:

Trong đó: x₁, x_n tương ứng là nghiệm nhỏ nhất của phương trình f(x)=g(x)

2. Ví dụ minh họa

Ví dụ 1: Tính diện tích S của hình phẳng giới hạn bởi Parabol (P):y=3-x², đường thẳng y=-2x+3, trục tung và x=1.

Lời giải:

Phương trình hoành độ giao điểm: 3-x²=-2x+3 ⇔ x²-2x=0

Diện tích cần tìm được tính bằng công thức sau đây:

Ví dụ 2: Tính diện tích S của hình phẳng giới hạn bởi các đường y=-2x² và y=-2x-4.

Lời giải:

Phương trình hoành độ giao điểm của y=-2x² và y=-2x-4 là:

-2x²=-2x-4 ⇔ -2x²+2x+4=0

Ví dụ 3: Tính diện tích S của hình phẳng giới hạn bởi các đường y=x³-3x và y=x

Lời giải:

Ta có phương trình hoành độ giao điểm x³-4x=0 

Diện tích

3. Bài tập vận dụng (có đáp án)

Bài 1: Tính diện tích hình phẳng được giới hạn bởi các đường y = 2x - x² và đường thẳng x + y = 2

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số y = x² + x - 1 và y = x⁴ + x - 1 là

x² + x - 1 = x⁴ + x - 1 ⇔ x² (x²-1)=0

Ta có: x² (x²-1) ≤ 0 ∀x ∈ [-1;1]. Do đó:

Bài 2: Tính diện tích S của hình phẳng giới hạn bởi các đường x³-x và y=x-x².

Lời giải:

Phương trình hoành độ giao điểm

x³-x=-x²+x ⇔ x=0; x=-2; x=1

Bài 3: Tính diện tích hình phẳng giới hạn bởi các đường y=cosx; Ox; Oy; x=π

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số y=cosx và trục Ox (y=0) là:

cosx=0 ⇔ x=π/2+kπ(k ∈ Z)

Xét trên [0;π] nên x=π/2.

Do đó

Bài 4: Tính Diện tích hình phẳng giới hạn bởi các đường y=e^x; y=1 và x=1

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=e^x và trục y=1 là:

e^x=1 ⇔ x=0.

Bài 5: Tính diện tích hình phẳng được giới hạn bởi các đường y=(e+1)x ,y=(1+e^x )x

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=(e+1)x và y=(1+e^x)x là:

(e+1)x = (1+e^x )x

Bài 6: Tính diện tích hình phẳng được giới hạn bởi các đường y=sin2x,y=cosx và hai đường thẳng x=0 ,x=π/2

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=sin2x và y=cosx là:

sin2x=cosx ⇔ cosx.(2sinx-1)=0

Xét trên [0;π/2] nên nhận x=π/6

Bài 7: Tính diện tích hình phẳng được giới hạn bởi hai đường y=√x và y=x²

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm sốy=√xvà y=x² là :

x²=√x ⇔ x=x⁴ ⇔ x⁴-x=0

Ta có: x²-√x ≤ 0,∀x ∈ [0;1]. Do đó:

Bài 8: Tính diện tích hình phẳng giới hạn bởi y=sinx; y=cosx; x=0; x=π

Lời giải:

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=sinx; y=cosx; x=0; x=π là:

sinx=cosx ⇔ tanx=1 ⇔ x=π/4+kπ,k ∈ Z

Vì x ∈ [0;π] nên x=π/4.

Ta có: sinx-cosx ≤ 0, ∀x ∈ [0;π/4]; sinx-cosx ≥ 0,∀x ∈ [π/4;π]

Bài 9: Tính diện tích hình phẳng giới hạn bởi

Lời giải:

Bài 10: Tính diện tích hình phẳng giới hạn bởi các đường 

Lời giải:

Phương trình hoành độ giao điểm của đồ thị hàm số y=2x và đồ thị hàm số y=8/x là

Diện tích hình phẳng cần tìm là:

4. Bài tập tự luyện (có đáp án)

Bài 1: Diện tích hình phẳng được giới hạn bởi đồ thị của hàm số y=x², trục hoành và hai đường thẳng x=-1, x=3 là:

A. 28/9         B. 28/3         C. 1/3         D. 7/3

Lời giải:

Đáp án : B

Giải thích :

Phương trình hoành độ giao điểm của đồ thị hàm số y=x² và trục hoành: x²=0 ⇔ x=0.

Mà hàm số y=x² không đổi dấu trên [-1;3] nên

Bài 2: Diện tích hình phẳng được giới hạn bởi đường y=x²-x+3 và đường thẳng y=2x+1 là

A. 7/6 (dvdt)        B. -1/6 (dvdt)

C. 1/6 (dvdt)        D. 5 (dvdt)

Lời giải:

Đáp án : C

Giải thích :

Phương trình hoành độ giao điểm của đồ thị hàm số y=x²-x+3 và đường thẳng y=2x+1 là

Ta có:

x²-3x+2 ≤ 0,∀x ∈ [1;2]. Do đó:

Bài 3: Diện tích hình phẳng được giới hạn bởi các đường y=lnx, trục hoành và hai đường thẳng x=1/e, x=e là

A. e+1/e (dvdt)        B. 1-1/e (dvdt)

C. e+1/e (dvdt)        D. 2-2/e (dvdt)

Lời giải:

Đáp án : D

Giải thích :

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=lnx và trục hoành là

lnx=0 ⇔ x=1

Ta có: lnx ≤ 0,∀x ∈ [1/e;1] và lnx ≥ 0,∀x ∈ [1;e].

Bài 4: Diện tích của hình phẳng giới hạn bởi (C):y=sinx;Ox ; x=0 ; x=π là

A. 1        B. 2        C. 3        D. 4

Lời giải:

Đáp án : B

Giải thích :

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=sinx và y=0 là

Ta có:sinx ≥ 0,∀x ∈ [0;π]. Do đó:

Bài 5: Diện tích hình phẳng giới hạn bởi y=x,y=sin² x+x (0 ≤ x ≤ π) có kết quả là

A. π        B. π/2        C. 2π        D. π/3

Lời giải:

Đáp án : B

Giải thích :

Phương trình hoành độ giao điểm của hai đồ thị hàm số y=sin² x+x và y=x là:

sin² x+x=x ⇔ sin² x=0 ⇔ x=kπ;k ∈ (Z).

Xét trên [0;π] nên nhận x=0;x=π.

Bài 6: Cho hình phẳng (H) được giới hạn bởi đường cong (C):y=e^x, trục Ox, trục Oy và đường thẳng x=2. Diện tích của hình phẳng (H) là

A. e+4        B. e²-e+2        C. e²/2 + 3        D. e²-1

Lời giải:

Đáp án : D

Giải thích :

Phương trình hoành độ giao điểm của đồ thị hàm số (C): y=e^x và trục Ox là

e^x=0(PTVN)

Bài 7: Cho hình phẳng (H) được giới hạn bởi đường cong (C):y=lnx, trục Ox và đường thẳng x=e. Diện tích của hình phẳng (H) là

A.1         B. 1/e - 1        C. e        D. 2

Lời giải:

Đáp án : A

Giải thích :

Phương trình hoành độ giao điểm của hai đồ thị hàm số (C):y=lnx và trục Ox:y=0 là: lnx=0 ⇔ x=1.

Ta có: lnx ≥ 0, ∀x ∈ [1;e].

Bài 8: Cho hình phẳng (H) được giới hạn đường cong (C):y=x³-2x² và trục Ox. Diện tích của hình phẳng (H) là

A. 4/3        B. 5/3        C. 11/12        D. 68/3

Lời giải:

Đáp án : A

Giải thích :

Phương trình hoành độ giao điểm của hai đồ thị hàm số(C):y=x³-2x²và trục Ox:y=0 là:

Ta có: x³-2x² ≤ 0, ∀x ∈ [0;2]. Do đó:

Bài 9: Diện tích hình phẳng giới hạn bởi các đường y=-x,y=2x-x² bằng

A. 4        B. 9/2        C. 5        D. 7/2

Lời giải:

Đáp án : A

Giải thích :

Phương trình hoành độ giao điểm:

Bài 10: Diện tích hình phẳng giới hạn bởi các đường y=x+3, y=x²-4x+3 bằng

A. 5²/6        B. 5³/6        C. 5⁴/6        D. (5³-1)/6

Lời giải:

Đáp án : B

Giải thích :

Phương trình hoành độ giao điểm:

Bài 11: Diện tích hình phẳng được giới hạn bởi y=sin² x+sinx+1; y=0; x=0; x=π/2 là 114

Lời giải:

Đáp án : B

Giải thích :

Bài 12: Diện tích hình phẳng giới hạn bởi các đường y=-1, y=x⁴-2x²-1 bằng

Lời giải:

Đáp án : C

Giải thích :

Bài 13: Diện tích hình phẳng giới hạn bởi các đường y=xe^x, y=0, x=1 bằng

A. -2         B. 2        C. -1         D.1

Lời giải:

Đáp án : D

Giải thích :

Bài 14: Diện tích hình phẳng giới hạn bởi các đường y=sin2x, y=0, x=0, x=π bằng

A. 2        B. 1        C. -1         D. -2

Lời giải:

Đáp án : A

Giải thích :

Bài 15: Diện tích hình phẳng giới hạn bởi các đường y=e^(2x-1), y=1, x=-2 bằng

Lời giải:

Đáp án : D

Giải thích :

Bài 16: Diện tích hình phẳng giới hạn bởi các đường (C):y = x(3-x)², y=0 và các đường thẳng x=2, x=4 bằng

A. 2        B. 3/2        C. 3        D. 1

Lời giải:

Đáp án : A

Giải thích :

Bài 17: Diện tích hình phẳng giới hạn bởi các đường (C):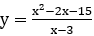 và hai trục toạ độ bằng:

Lời giải:

Đáp án : A

Giải thích :

Bài 18: Diện tích hình phẳng giới hạn bởi các đường (C):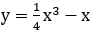 và tiếp tuyến của (C)tại điểm có hoành độ bằng-2, bằng:

A. 27        B. 21        C. 11        D. 2

Lời giải:

Đáp án : A

Giải thích :

Bài 19: Diện tích hình phẳng giới hạn bởi các đường (C):y=x²-2x+2, tiếp tuyến của (C) tại giao điểm của (C) với trục tung và các đường thẳng x=3, y=0 bằng

A. 5        B. 6        C. 9        D. 21

Lời giải:

Đáp án : C

Giải thích :

Bài 20: Diện tích hình phẳng giới hạn bởi các đường y=x³, y=2-x², x=0 bằng:

A. 17/12        B. -5/12        C.0        D. 12/17

Lời giải:

Đáp án : D

Giải thích :

Xem thêm các dạng bài tập toán hay khác:

40 Bài tập Ứng dụng của tích phân tính thể tích khối tròn xoay (2024) cực hay, có đáp án chi tiết

30 Bài tập Tính tích phân bằng phương pháp đổi biến số loại 1 (2024) cực hay, có đáp án

30 Bài tập Tính tích phân từng phần (2024) cực hay, có đáp án

20 Bài tập Tính tích phân hàm chứa dấu giá trị tuyệt đối (2024) chi tiết, có đáp án

30 Bài tập Tính tích phân hàm số chẵn, hàm số lẻ (2024) cực hay, có đáp án