30 Bài tập đường trung tuyến trong tam giác vuông cân (2024) hay, có đáp án

Đường trung tuyến trong tam giác vuông cân  

Lý thuyết

1. Đường trung tuyến hình tam giác là gì?

- Đường trung tuyến trong tam giác là một đường thẳng đi qua trung điểm của cạnh đối diện với góc mà đường trung tuyến bắt đầu.

- Trung điểm của đường trung tuyến chính là điểm chia đoạn thẳng thành hai phần bằng nhau và một tam giác có 3 đường trung tuyến

Ví dụ: Cho tam giác ABC, có D, E, F lần lượt là trung điểm của các cạnh AC, AB, BC. Từ đó ta có các đường thẳng BD, AF, CE là các đường trung tuyến của tam giác ABC.

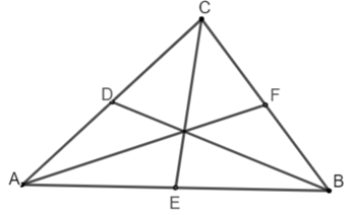
2. Tính chất của đường trung tuyến trong tam giác

– Định lý 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm gặp nhau của ba đường trung tuyến gọi là trọng tâm của tam giác đó.

– Định lý 2: Vị trí trọng tâm: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng 2/3 độ dài đường trung tuyến đi qua đỉnh ấy.

– Tính chất 1: Khoảng cách từ trọng tâm đến trung điểm của mỗi cạnh bằng 1/3 độ dài đường trung tuyến tương ứng với cạnh đó

– Tính chất 2: Mỗi trung tuyến chia diện tích của tam giác thành hai phần bằng nhau. Ba trung tuyến chia tam giác thành sáu tam giác nhỏ với diện tích bằng nhau.

Ví dụ: Cho tam giác ABC, có D, E, F lần lượt là trung điểm  của các cạnh AC, AB, BC.

- Gọi G là giao điểm của các đường thẳng BD, AF, CE, suy ra G là trọng tâm của tam giác ABC. Ta có tính chất sau: 

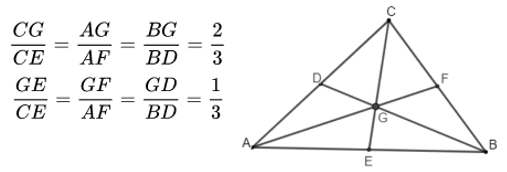
3. Tính chất đường trung tuyến trong tam giác vuông cân

- Tam giác vuông cân là một tam giác có một góc vuông với hai cạnh góc vuông bằng nhau và bằng a.

- Trung tuyến trong tam giác vuông cân sẽ nối từ góc vuông đến cạnh đối diện sẽ là một đoạn thẳng vuông góc với cạnh huyền và bằng một phần hai nó.

Hay nói cách khác, cách nhận biết đường trung tuyến của một tam giác vuông cân là từ góc vuông, ứng với cạnh huyền sẽ có các tính chất của đường trung tuyến của tam giác vuông và tam giác cân, tức là nó sẽ có chiều dài bằng 1/2 cạnh huyền, vuông góc với cạnh huyền, và chia góc vuông thành 2 góc có 45^o. 

4. Công thức tính trung tuyến tam giác vuông cân

Tam giác vuông cân là một tam giác có một góc vuông với hai cạnh góc vuông bằng nhau và bằng a. Do đó, trung tuyến trong tam giác vuông cân mà nối từ góc vuông đến cạnh đối diện sẽ là một đoạn thẳng vuông góc với cạnh huyền và bằng một phần hai nó.

Độ dài trung tuyến = (a)/2

5. Công thức tính độ dài đường trung tuyến

Công thức tính độ dài đường trung tuyến của cạnh bất kỳ bằng căn bậc 2 của một phần hai tổng bình phương hai cạnh kề trừ một phần tư bình phương cạnh đối.

Trong đó: a, b ,c lần lượt là các cạnh trong tam giác

                 m_a, m_b, m_c lần lượt là những đường trung tuyến trong tam giác  

Ví dụ minh họa

Ví dụ 1. Cho tam giác ABC có G là trọng tâm tam giác, N là trung điểm AC. Khi đó BG/BN là bao nhiêu.

Hướng dẫn:

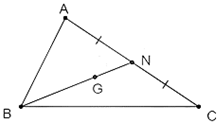
Vì G là trọng tâm của $\Delta ABC$ nên $BG=\frac{2}{3}BN$

Số thích hợp điền vào chỗ trống là $\frac{2}{3}$

Ví dụ 2. Cho hình vẽ sau: Biết MG = 3cm. Tính MR, NG

Hướng dẫn:

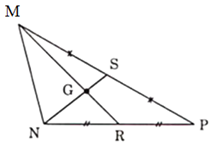
a) Ta có: MR, NS là hai đường trung tuyến của tam giác MNP và chúng cắt nhau tại G nên G là trọng tâm tam giác MNP

Theo tính chất ba đường trung tuyến của tam giác ta có: $\frac{MG}{MR}=\frac{2}{3}\Rightarrow MR=\frac{3}{2}MG=\frac{3}{2}.3=4,5\left(cm\right)$

Vậy MR = 4,5cm

b) Theo câu trước ta có G là trọng tâm của tam giác MNP.

Theo tính chất ba đường trung tuyến của tam giác ta có:

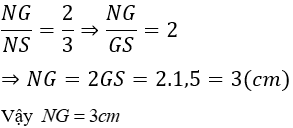
Ví dụ 3. Tam giác ABC có trung tuyến AM = 9cm và G là trọng tâm. Độ dài đoạn AG là

Hướng dẫn:

Vì G là trọng tâm của tam giác ABC và AM là đường trung tuyến nên $AG=\frac{2}{3}AM$ (tính chất ba đường trung tuyến của tam giác)

Do đó: $AG=\frac{2}{3}.9=6cm$

Bài tập vận dụng

Bài 1: Cho tam giác MNP cân tại M, biết MN = MP = 8cm, NP = 7cm. Kẻ đường tuyến MI. Chứng minh MI ⊥ NP

Lời giải

Ta có MI là đường trung tuyến của ∆MNP nên IN = IP

Mặt khác ∆MNP là tam giác cân tại M

=> MI vừa là đường trung tuyến vừa là đường cao

=> MI ⊥ NP

Bài 2: Cho tam giác MNP biết NP = 20cm, PM = 16cm, MN = 14cm. Tính độ dài các đường trung tuyến của tam giác MNP

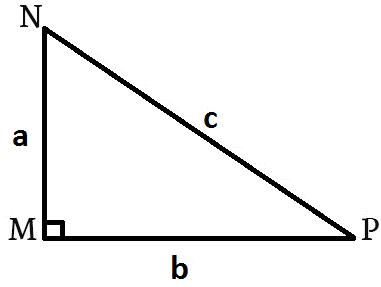
Lời giải

a = NP = 20cm, b = PM = 16cm, c = MN = 14cm

Gọi độ dài đường trung tuyến từ những đỉnh M, N, P của ∆MNP lần lượt là m_a, m_b, m_c

Áp dụng công thức tính đường trung tuyến trong tam giác ta có:

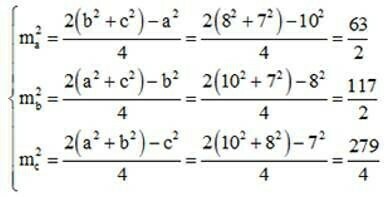
Vì độ dài các đường trung tuyến là độ dài đoạn thẳng do đó:

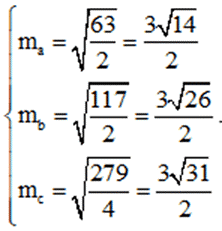
Bài 3: Cho tam giác vuông ABC có hai góc vuông AB = 3cm, AC= 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.

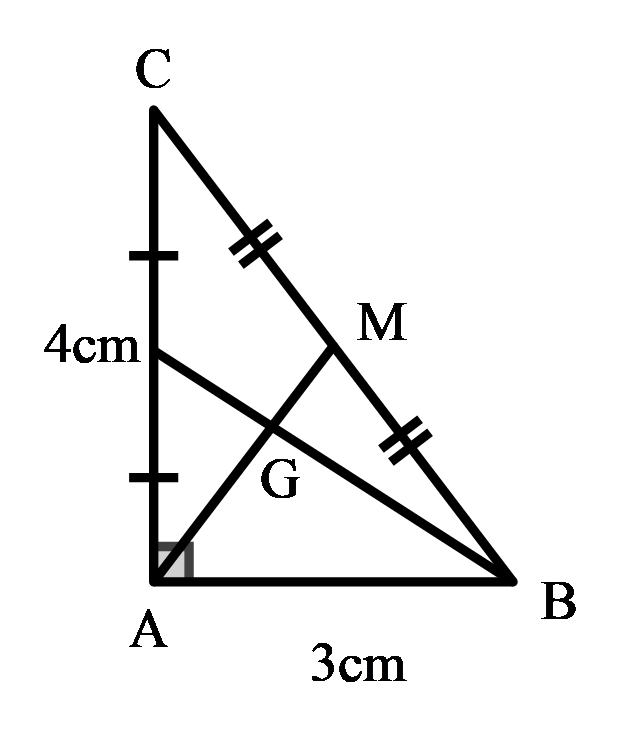
Xét ΔABC vuông tại A, ta có:

 BC² = AB² + AC² (định lí Pitago)

Thay số:  BC² = 3² + 4² = 25

 ⇒ BC = 5 (cm)

Gọi M là trung điểm của BC, suy ra AM là đường trung tuyến.

Vì theo đề bài: Trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên

$AM=\frac{1}{2}BC=\frac{1}{2}.5=2,5\left(cm\right)$

Vì G là trọng tâm tam giác ABC nên $AG=\frac{2}{3}AM=\frac{2}{3}.2,5=\frac{5}{3}\left(cm\right)$

Bài 4: Cho tam giác $ABC$ vuông cân tại $A,$ đường trung tuyến $BM.$ Gọi $D$ là hình chiếu của $C$ trên $BM$, $H$ là hình chiếu của $D$ trên $AC.$ Chứng minh rằng $AH=3HD.$

Lời giải

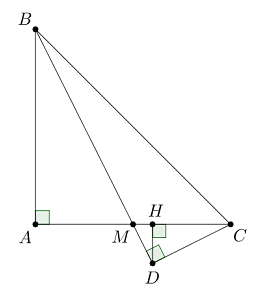
Xét tam giác $ABM$và tam giác $HCD$ ta có:

+ $\widehat{BAM}=\widehat{DHC}={90}^0$ (gt)

            + $\{\begin{array}{l}\widehat{ABM}={90}^0-\widehat{BMA}\\ \widehat{HCD}={90}^0-\widehat{DMC}\\ \widehat{BMA}=\widehat{DMC}\left(dd\right)\end{array}\Rightarrow \widehat{ABM}=\widehat{HCD}$.

$\begin{array}{l}\Rightarrow \mathrm{\Delta }ABM\sim \mathrm{\Delta }HCD\left(g.g\right)\\ \Rightarrow {\displaystyle \frac{AB}{HC}}={\displaystyle \frac{AM}{HD}}\Rightarrow {\displaystyle \frac{HC}{HD}}={\displaystyle \frac{AB}{AM}}=2\Rightarrow HC=2HD.\end{array}$

Xét tam giác $MCD$vuông tại $D$, đường cao $DH$ ta có:

$H{D}^2=MH.HC=MH.2HD$  (hệ thức lượng trong tam giác vuông).

$\begin{array}{l}\Rightarrow MH=0,5HD\\ \Rightarrow AM=MC=MH+HC=0,5HD+2HD=2,5HD\\ \Rightarrow AH=AM+MH=2,5HD+0,5HD=3HD.\end{array}$

Bài 5: Tam giác vuông cân tại A có AB = 2a. Đường trung tuyến BM có độ dài bằng bao nhiêu?

Lời giải

+ Ta có: AB = AC = 2a

+ Ta có: $BC=\sqrt{A{B}^2+A{C}^2}=\sqrt{4a^2+4a^2}=2\sqrt{2}a$

$$\begin{gathered} M{B}^2=\frac{B{C}^2+A{B}^2}{2}-\frac{A{C}^2}{4} \\ =\frac{8a^2+4a^2}{2}-\frac{4a^2}{4}=5a^2 \\ \Rightarrow MB=a\sqrt{5} \end{gathered}$$

Xem thêm các dạng bài tập Toán liên quan khác:

70 Bài tập về Tính chất ba đường trung tuyến của tam giác (có đáp án năm 2024)

70 Bài tập về Sự đồng quy của ba đường trung tuyến trong một tam giác (có đáp án năm 2024)

70 Bài tập về Sự đồng quy của ba đường trung trực trong một tam giác (có đáp án năm 2024)

70 Bài tập về Sự đồng quy của ba đường cao trong một tam giác (có đáp án năm 2024)

70 Bài tập về Sự đồng quy của ba đường phân giác trong một tam giác (có đáp án năm 2024)