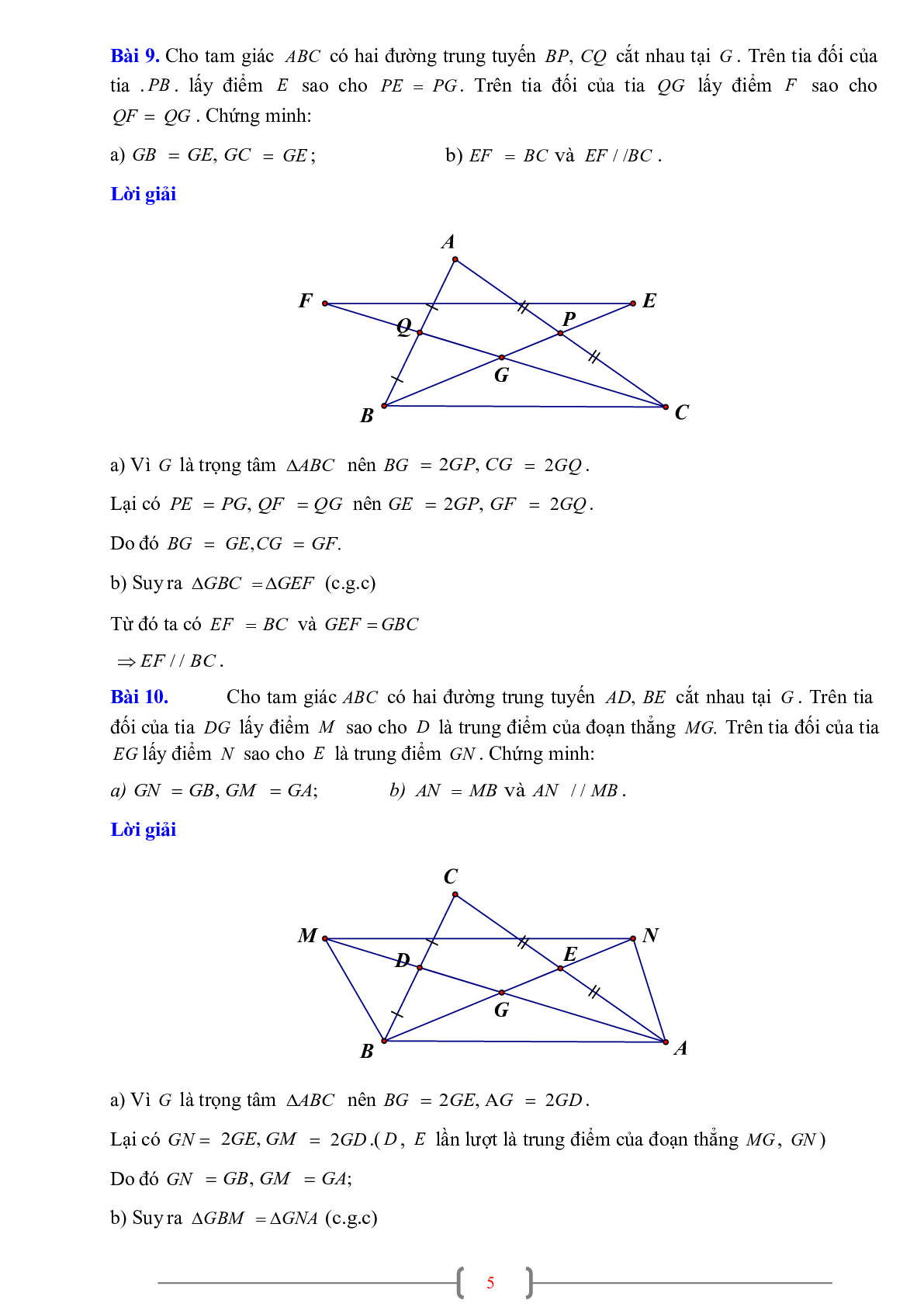
Sự đồng quy của ba đường trung tuyến trong một tam giác
1. Kiến thức cần nhớ
a) Đường trung tuyến của tam giác
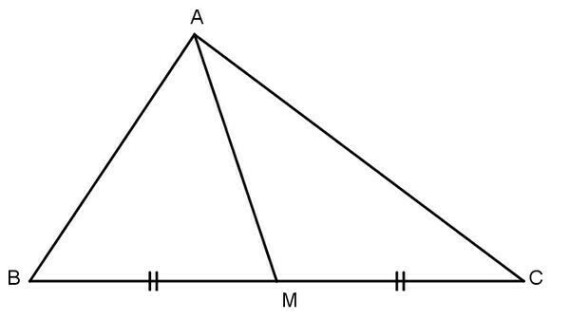
Trong hình dưới đây, đoạn thẳng AM nối đỉnh A của tam giác ABC với trung điểm M của cạnh BC gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc ứng với cạnh BC) của tam giác ABC.
b) Sự đồng quy của ba đường trung tuyến
Định lí 1: Ba đường trung tuyến của một tam giác cùng đi qua một điểm (hay đồng quy tại một điểm). Điểm đó cách mổi đỉnh một khoảng bằng độ dài đường trung tuyến đi qua đỉnh ấy.
Ví dụ: Trong tam giác ABC có các đường trung tuyến AM, BN, CP đồng quy tại điểm G.
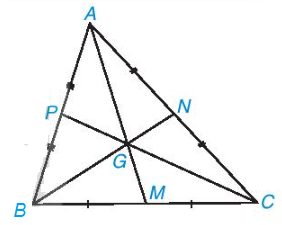
Ta có:
Chú ý: Điểm đồng quy của ba đường trung tuyến gọi là trọng tâm tam giác.
Ví dụ: Tam giác ABC có các đường trung tuyến AM, BN, CP đồng quy tại điểm G.
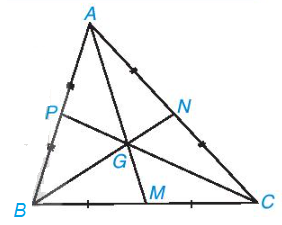
Khi đó, G được gọi là trọng tâm tam giác ABC.
2. Các dạng bài tập về Sự đồng quy của ba đường trung tuyến
Dạng 1. Sử dụng tính chất trọng tâm của tam giác
Phương pháp giải:
Sử dụng linh hoạt các tỉ số liên quan đến trọng tâm tam giác
Dạng 2. Chứng minh một điểm là trọng tâm của tam giác
Phương pháp giải:
Để chứng minh một điểm là trọng tâm của tam giác, ta có thể dùng một trong hai cách sau:
+ Chứng minh điểm đó là giao điểm của hai đường trung tuyến trong tam giác.
+ Chứng minh điểm đó thuộc một đường trung tuyến của tam giác và thỏa mãn một trong các tỉ lệ về tính chất trọng tâmcủa tam giác.
Dạng 3. Vấn đề đường trung tuyến trong tam giác vuông, tam giác cân, tam giác đều
Phương pháp giải:
Chú ý những tính chất của tam giác vuông, tam giác cân, tam giác đều.
3. Bài tập tự luyện (có hướng dẫn)
(Xem chi tiết trong file đính kèm bên dưới)
Xem thêm các dạng bài tập Toán đầy đủ và hay khác:
70 Bài tập về Sự đồng quy của ba đường trung tuyến trong một tam giác (có đáp án năm 2024)
70 Bài tập về Sự đồng quy của ba đường phân giác trong một tam giác (có đáp án năm 2024)
70 Bài tập về Sự đồng quy của ba đường trung trực trong một tam giác (có đáp án năm 2024)
70 Bài tập về Sự đồng quy của ba đường cao trong một tam giác (có đáp án năm 2024)