Tính chất ba đường trung tuyến của tam giác

A. Kiến thức cần nhớ

1. Đường trung tuyến của tam giác

– Trong tam giác ABC (hình bên dưới), đoạn thẳng AM nối đỉnh A với trung điểm M của cạnh BC được gọi là đường trung tuyến (xuất phát từ đỉnh A hoặc tương ứng với cạnh BC).

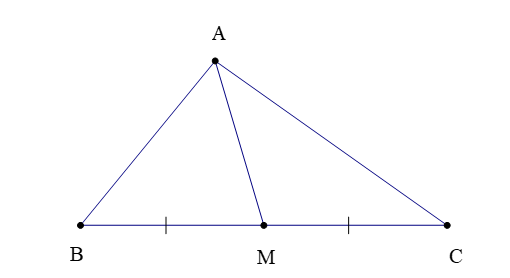
Đôi khi, đường thẳng AM cũng được gọi là đường trung tuyến của ∆ABC.

Ví dụ: Quan sát hình bên dưới và cho biết trong hình có bao nhiêu đường trung tuyến?

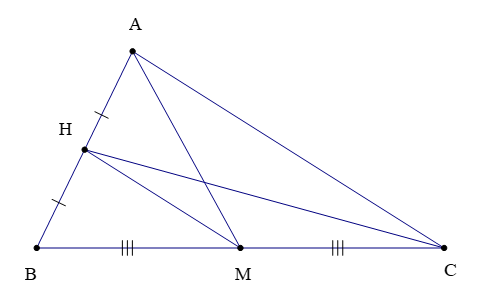
Hướng dẫn giải

Quan sát hình vẽ ta có:

• A là đỉnh của ∆ABC và M là trung điểm của BC nên đoạn thẳng AM là đường trung tuyến của ∆ABC.

• C là đỉnh của ∆ABC và H là trung điểm của AB nên đoạn thẳng CH là đường trung tuyến của ∆ABC.

• M là đỉnh của ∆ABM và H là trung điểm của AB do đó MH là đường trung tuyến của ∆ABM.

• H là đỉnh của ∆HBC và M là trung điểm của BC nên đoạn thẳng HM là đường trung tuyến của ∆HBC.

Vậy trong hình vẽ trên có tất cả 4 đường trung tuyến.

– Chú ý: Mỗi tam giác có ba đường trung tuyến.

Ví dụ: Tam giác ABC (hình vẽ dưới) có ba đường trung tuyến là AM, BK và CN.

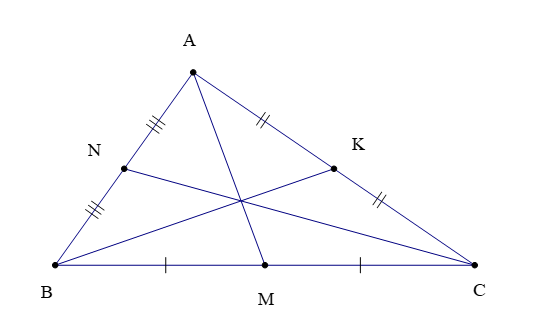
2. Tính chất ba đường trung tuyến của tam giác

– Ba đường trung tuyến của một tam giác cùng đi qua một điểm. Điểm đó được gọi là trọng tâm của tam giác.

Chú ý: Trong tam giác ABC (hình vẽ dưới) có ba đường trung tuyến AM, BK, CN cùng đi qua điểm G, ta còn nói chúng đồng quy tại điểm G.

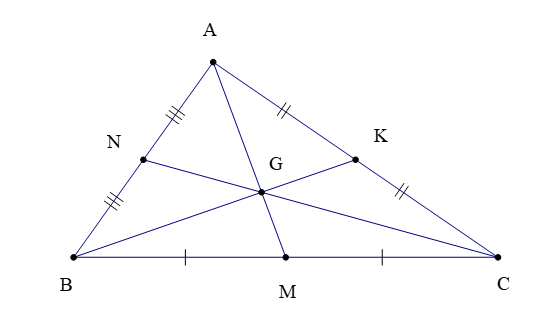
Để xác định trọng tâm của một tam giác, ta chỉ cần vẽ hai đường trung tuyến bất kì và xác định giao điểm của hai đường đó.

Nhận xét: Trọng tâm của một tam giác cách mỗi đỉnh một khoảng bằng $\frac{2}{3}$ độ dài đường trung tuyến đi qua đỉnh ấy.

Lưu ý: Trong ∆ABC, với AM là đường trung tuyến và G là trọng tâm ta có:

$\frac{\text{GM}}{\text{AM}}=\frac{1}{3},\frac{\text{GM}}{\text{GA}}=\frac{1}{2}$

Ví dụ: Cho ∆ABC như hình vẽ, biết AM = 18 cm và BN = 21 cm.

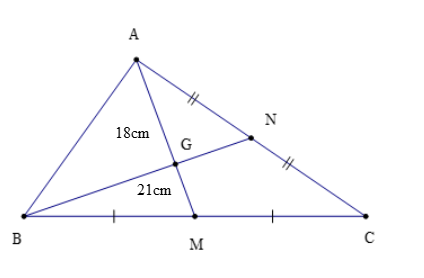
a) Chứng minh: G là trọng tâm của ∆ABC.

b) Tính độ dài AG, GN.

Hướng dẫn giải

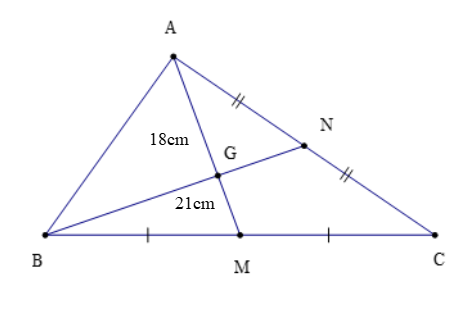
Theo hình vẽ trên ta có:

A là đỉnh của ∆ABC và M là trung điểm của BC nên đoạn thẳng AM là đường trung tuyến của ∆ABC.

B là đỉnh của ∆ABC và N là trung điểm của AC nên đoạn thẳng BN là đường trung tuyến của ∆ABC.

Mà hai đường trung tuyến AM và BN cắt nhau tại G do đó G là trọng tâm của ∆ABC.

Vậy G là trọng tâm của ∆ABC.

b) Theo phần a ta có: G là trọng tâm của ∆ABC nên $\text{AG = }\frac{2}{3}\text{AM}$ (tính chất trọng tâm của tam giác)

Hay $\text{AG = }\frac{2}{3}.18=12\left(\mathrm{cm}\right)$

Vì BN là đường trung tuyến của ∆ABC và G là trọng tâm của ∆ABC

Suy ra $\frac{\text{GN}}{\text{BN}}=\frac{1}{3}$ hay $\text{GN = }\frac{1}{3}\text{BN = }\frac{1}{3}.21=7\left(\text{cm}\right)$

Vậy AG = 12 cm, GN = 7 cm.

B. Các dạng bài tập Tính chất ba đường trung tuyến của tam giác

Dạng 1: Sử dụng tính chất trọng tâm tam giác.

– Ba đường trung tuyến của tam giác đồng quy tại một điểm. Điểm này gọi là trọng tâm của tam giác.

– Trọng tâm của tam giác cách mỗi đỉnh một khoảng bằng 2 3 độ dài đường trung tuyến đi qua đỉnh ấy.

Bước 1. Xác định trọng tâm nằm trên đường trung tuyến nào.

Bước 2. Sử dụng linh hoạt tỉ lệ khoảng cách từ trọng tâm đến hai đầu đoạn thẳng trung tuyến.

Dạng 2: Chứng minh một điểm là trọng tâm tam giác.

Sử dụng tính chất trọng tâm. Chẳng hạn để chứng minh G là trọng tâm tam giác ABC, có ba đường trung tuyến AD, BE, CF thì ta chứng minh.

Cách 1. G AD và 2 3 GA AD hoặc G BE và 2 3 GB BE hoặc G CF và 2 3 GC CF.

Cách 2. Chứng minh G là giao điểm của hai trong ba đường trung tuyến của tam giác ABC.

Dạng 3: Đường trung tuyến của tam giác cân, tam giác đều, tam giác vuông.

Chú ý đến tính chất của tam giác cân, tam giác đều và tam giác vuông.

C. Bài tập tự luyện 

1. Bài tập vận dụng

1.1. Bài tập tự luận

Bài 1. Cho ∆ABC có hai tiếp tuyến BM và CN cắt nhau tại trọng tâm G. Chứng minh rằng: BC < $\frac{2}{3}\left(\text{BM + CN}\right).$

Hướng dẫn giải

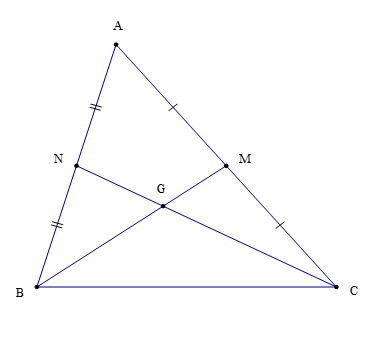
Theo bài ta có: G là trọng tâm của ∆ABC.

Suy ra $\text{BG = }\frac{2}{3}\text{BM; CG = }\frac{2}{3}\text{CN}$ (tính chất trọng tâm của tam giác)

Xét ∆BGC ta có: BG + CG > BC (bất đẳng thức tam giác)

Hay $\frac{2}{3}\text{BM +}\frac{2}{3}\text{CN > BC}$

Suy ra BC < $\frac{2}{3}\left(\text{BM + CN}\right)$

Vậy BC < $\frac{2}{3}\left(\text{BM + CN}\right).$

Bài 2. Cho ∆ABC nhọn (AB < AC), đường trung tuyến AO. Trên tia đối của tia OA lấy điểm D sao cho OA = OD. Chứng minh rằng: AC // BD.

Hướng dẫn giải

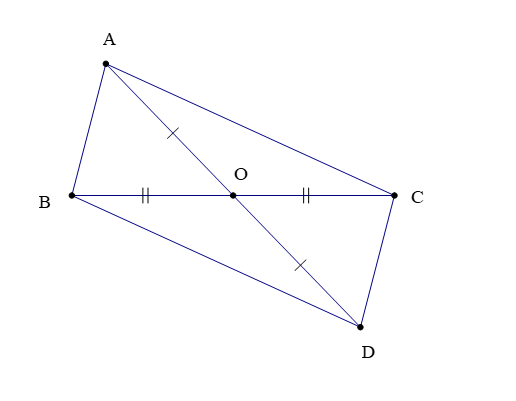
Theo bài ta có AO là trung tuyến của ∆ABC nên BO = CO.

Xét ∆AOC và ∆DOB có:

AO = DO (giả thiết),

$\widehat{\text{AOC}}=\widehat{\text{DOB}}$ (hai góc đối đỉnh),

OC = OB (chứng minh trên).

Do đó ∆AOC = ∆DOB (c.g.c)

Suy ra $\widehat{\text{CAO}}=\widehat{\text{BDO}}$ (hai góc tương ứng) 

Hay $\widehat{\mathrm{CAD}}=\widehat{\mathrm{BDA}}$

Mà hai góc này ở vị trí so le trong           

Suy ra AC // BD

Vậy AC // BD.

Bài 3. Cho ∆ABC vuông tại A có AB = 9 cm; BM là đường trung tuyến và G là trọng tâm của tam giác. Kẻ AH ⊥ BM tại H. Tính AM biết rằng S_DABG = 12 cm².

Hướng dẫn giải

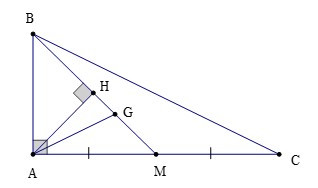
Vì ∆ABC có BM là đường trung tuyến và G là trọng tâm nên ta có: $\text{BG = }\frac{2}{3}\text{BM}$  (1)

Ta có ${\mathrm{S}}_{\mathrm{\Delta ABG}}=\frac{1}{2}\mathrm{AH}.\mathrm{BG}$  (2)

${\mathrm{S}}_{\mathrm{\Delta ABM}}=\frac{1}{2}\text{AH.BM}$   (3)

Từ (1), (2) và (3) ta có:

$\frac{{\displaystyle {\text{S}}_{\mathrm{\Delta AB}\text{G}}}}{{\displaystyle {\text{S}}_{\mathrm{\Delta AB}\text{M}}}}=$ $\frac{\frac{1}{2}\text{AH.BG}}{\frac{1}{2}\text{AH.BM}}=\frac{\frac{1}{2}\text{AH.}\frac{2}{3}\text{BM}}{\frac{1}{2}\text{AH.BM}}=\frac{2}{3}$

Suy ra 2S_DABM = 3S_DABG

Do đó ${\text{S}}_{\mathrm{\Delta AB}\text{M}}=\frac{3}{2}{\text{S}}_{\mathrm{\Delta AB}\text{G}}=\frac{3}{2}.12=18{\text{(cm}}^2\text{)}$

Ta lại có ${\text{S}}_{\mathrm{\Delta AB}\text{M}}=\frac{1}{2}\text{AB.AM}$(vì ∆ABM vuông tại A)

Hay $18=\frac{1}{2}\mathrm{.9.}\text{ AM}$ 

Suy ra AM = $\frac{18.2}{9}$= 4 (cm)

Vậy AM = 4 cm.

1.2. Bài tập trắc nghiệm 

Câu 1. Cho ∆ABC có ba đường trung tuyến AX, BY, CZ cắt nhau tại G. Biết GA = GB = GC. Hãy so sánh GX, GY và GZ.

A. GX > GY > GZ;                   

B. GX = GY = GZ;                   

C. GX < GY = GZ;                   

D. GX = GY > GZ.

Hướng dẫn giải

Đáp án đúng là: B

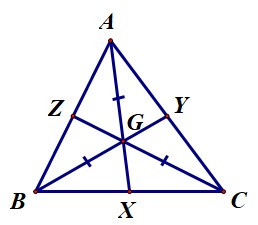
Vì G là trọng tâm của ∆ABC nên theo tính chất trọng tâm ta có:

$\frac{\mathrm{GX}}{\mathrm{GA}}=\frac{1}{2}$, $\frac{\mathrm{GY}}{\mathrm{GB}}=\frac{1}{2}$, $\frac{\mathrm{GZ}}{\mathrm{GC}}=\frac{1}{2}$ 

Suy ra $\mathrm{GX}=\frac{1}{2}\mathrm{GA};\mathrm{GY}=\frac{1}{2}\mathrm{GB};\mathrm{GZ}=\frac{1}{2}\mathrm{GC}$

Mà GA = GB = GC.

Suy ra GX = GY = GZ.

Vậy ta chọn đáp án B.

Câu 2. Cho ∆ABC có G là trọng tâm như hình bên.

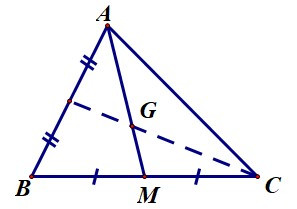
Tìm x, biết AG = 4x + 6 và AM = 9x.

A. x = 4;                

B. x = 1;                

C. x = 2;                

D. x = 3.

Hướng dẫn giải

Đáp án đúng là: D

Ta có G là trọng tâm của ∆ABC.

Suy ra $\mathrm{AG}=\frac{2}{3}\mathrm{AM}$.

Do đó $4\mathrm{x}+6=\frac{2}{3}.9\mathrm{x}$

4x + 6 = 2.3x

4x + 6 = 6x

4x – 6x = –6

–2x = –6.

x = –6 : (–2)

x = 3.

Vậy ta chọn đáp án D.

Câu 3. Cho ∆ABC, hai đường trung tuyến BM và CN cắt nhau tại G. Trên tia GB và GC lấy các điểm F và E sao cho G là trung điểm của FM, đồng thời là trung điểm của EN. Khẳng định nào sau đây sai?

A. GF = FB;         

B. E là trung điểm GC;             

C. NG > EC;                   

D. AD, BE, CF đồng quy tại một điểm.

Hướng dẫn giải

Đáp án đúng là: C

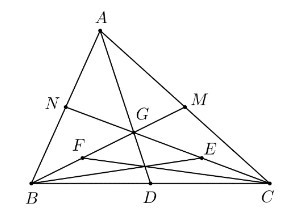
Do ∆ABC có hai đường trung tuyến BM và CN cắt nhau tại G nên G là trọng tâm của ∆ABC

Suy ra $\mathrm{GM}=\frac{1}{2}\mathrm{GB}$ 

Mà G là trung điểm của FM nên GM = GF

Do đó $\mathrm{GF}=\frac{1}{2}\mathrm{GB}$

Suy ra F là trung điểm của GB.

Nên GF = FB. Do đó A đúng.

Chứng minh tương tự ta có E là trung điểm của GC. Do đó B đúng.

Ta có: GN = GE = EC nên C là sai.

Vì F, E lần lượt là trung điểm của GB và GC (chứng minh trên)

Nên CF, BE là hai đường trung tuyến của ∆GBC.

Mà ∆GBC còn có GD là đường trung tuyến thứ ba (D là trung điểm BC).

Khi đó GD, BE, CF đồng quy tại trọng tâm của ∆GBC.

Hay AD, BE, CF đồng quy tại một điểm.

Do đó đáp án D đúng.

Vậy ta chọn đáp án C.

2. Bài tập tự luyện có hướng dẫn