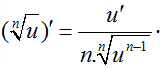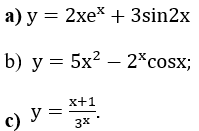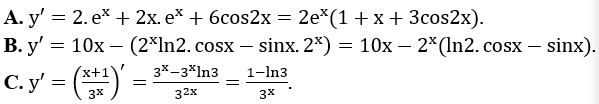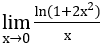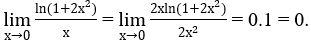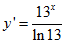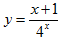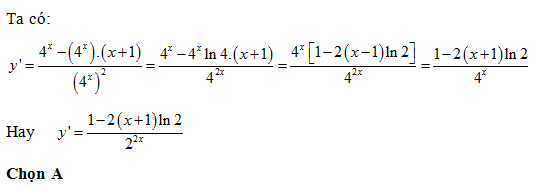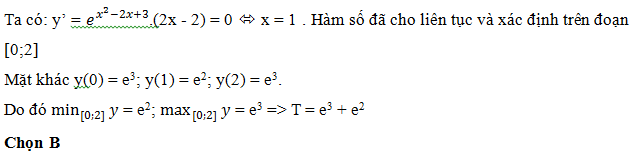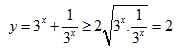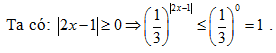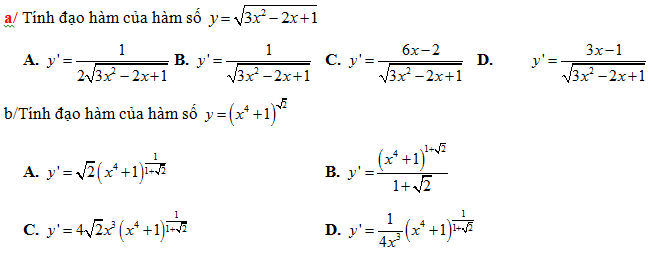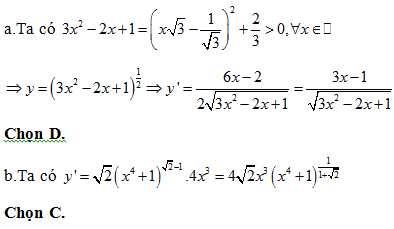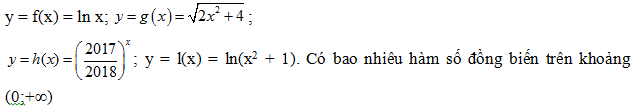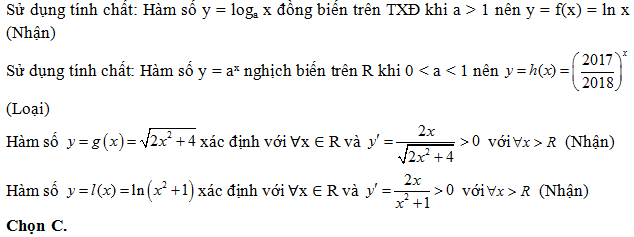Bài tập về các công thức hàm số mũ
I. Lý thuyết
Hàm số mũ: y = ax, (a > 0, a ≠ 1)
Tập xác định: D = R
Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = af(x) thì t > 0
Tính đơn điệu:
+ Khi a > 1 thì hàm số y = ax đồng biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) > g(x).
+ Khi 0 < a < 1 thì hàm số y = ax nghịch biến, khi đó ta luôn có: af(x) > ag(x) ⇔ f(x) < g(x).
Đạo hàm:
(ax)' = ax.ln a ⇒ (au)' = u'.au.ln a
(ex)' = ex ⇒ (eu)' = eu.u'
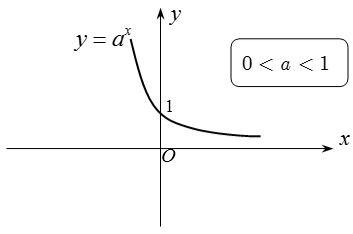
Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.
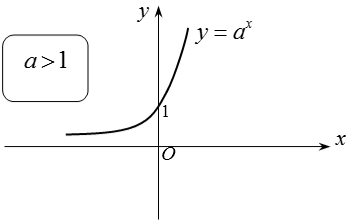

II. Ví dụ minh họa
Ví dụ 1: Tính đạo hàm của các hàm số sau:
Lời giải:
Ví dụ 2: Tìm giới hạn sau
Lời giải:
III. Bài tập vận dụng
Bài 1: a/ Đạo hàm của hàm số y = 3x.xx là:
A. y’ = (ln 3x + 3).x2.3x B. y’ = (ln 3 + 3).x2.3x
C. y’ = (xln 3 + 3).x3.3x D. y’ = (ln 3x + 1).x3.3x
b/ Tính đạo hàm của hàm số y = 13x
A. y’ = x.13x-1
B. y’ = 13xln 13
C. y’ = 13x
D.
Lời giải:
a/ ta có: y’ = 3x.ln 3.x3 + 3x.3x2 = x2.3x (xln 3 + 3) = x2.3x.(ln 3x + 3)
Chọn A
b/ Ta có: y’ = 13x ln 13
Chọn B
Bài 2: Tính đạo hàm của hàm số
Lời giải:
Bài 3: a/ Đạo hàm của hàm số y = ex2.sin x là:
A. y’ = ex2(2x sin x – cos x) B. y’ = ex2(2x.sin x +cos x)
C. y’ = ex2(sin x – cos x) D. y’ = ex2(sin x + cos x)
b/ Đạo hàm của hàm số f(x) = x3.3x là:
A. f’(x) = (3 + ln 3).x2.3x B. f’(x) = x3.3x(3 + xln 3)
C. f’(x) = (3 + ln 3x).x2.3x D. f’(x) = x3.3x(3 + ln 3)
Lời giải:
a/ Ta có: y’ = ex2.2x.sin x + ex2.cos x = ex2(2x.sin x + cos x)
Chọn B
b/ Ta có: f’(x) = 3x2.3x + x3.3xln 3 = x2.3x(3 + xln 3)
Chọn C
Bài 4: Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = ex2-2x+3 trên đoạn [0;2] là:
A. e3 – e B. e3 – e2 C. e3 D. e3 + e
Lời giải:
Bài 5: Cho hàm số y = 3x + 3-x. Khẳng định nào sau đây là đúng.
A. Giá trị nhỏ nhất của hàm số là 0 và hàm số không có giá trị lớn nhất.
B. Hàm số không có giá trị lớn nhất và giá trị nhỏ nhất.
C. Giá trị nhỏ nhất của hàm số là 2 và giá trị lớn nhất của làm số là 3
D. Giá trị nhỏ nhất của hàm số là 2 và hàm số không có giá trị lớn nhất.
Lời giải:
Âp dụng bất đẳng thức cosi; ta có:
nên giá trị nhỏ nhất của hàm số là 2
Hàm số đã cho không có giá trị lớn nhất vì limx→+∞y = +∞
Chọn D
Bài 6: Cho hàm số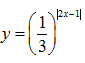
A. Giá trị nhỏ nhất của hàm số là 0 và hàm số không có giá trị lớn nhất.
B. Hàm số không có giá trị nhỏ nhất và giá trị lớn nhất của hàm số là 0
C. Giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất.
D. Hàm số không có giá trị nhỏ nhất và giá trị lớn nhất của hàm số là 1 .
Lời giải:
Do đó giá trị lớn nhất của hàm số là 1 và hàm số không có giá trị nhỏ nhất
Chọn D
Bài 7: Cho hàm số y = xex. Đẳng thức nào sau đây là đúng.
A. y’’ = 2y’ – y B. y’’ = y’ – 2y C. y’’ = 2xy’ – y D. y’’ = 2y’ – xy
Lời giải:
Ta có: y’ = ex + xex ⇒ y’’ = ex + ex + xex = 2ex + xex
Do đó: y’’ = 2y’ – y
Chọn A
Bài 8: Phát biểu nào sau đây sai?
A. Hai hàm số y = ax và y = loga x (a > 1) có cùng tình đơn điệu trên TXĐ.
B. Đồ thị hàm số y = ax (a > 0, a ≠ 1) luôn nằm trên trục hoành
C. Đồ thị hàm số y = loga x (a > 0, a ≠ 1) luôn nằm bên phải trục tung
D. Hai hàm số y = ax và y = loga x (0 < a < 1) đều có đồ thị nằm phía trên trục hoành.
Lời giải:
Căn cứ vào tính chất của đồ thị hàm mũ ta rút ra kết quả là đáp án D
+ Hai hàm số y = ax và y = loga x (a > 1) cùng đồng biến trên TXĐ
+ ax > 0; ∀x ∈ R nên đồ thị luon nằm trên Ox
+ y = loga x có có TXĐ D = (0;+∞) nên đồ thị luôn nằm bên phải trục tung
Chon D.
Bài 9
Lời giải:
Bài 10: Cho bốn hàm số sau:
A. 1 B. 2 C. 3 D. 4
Lời giải:
Xem thêm các dạng câu hỏi và bài tập liên quan khác:
30 bài tập về biến thiên hàm số mũ, hàm số lũy thừa, logarit 2024 (có đáp án)
30 Bài tập về đồ thị hàm số mũ (2024) có đáp án
Tìm tập xác định của hàm số mũ, lũy thừa, lôgarit mới nhất 2024