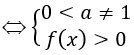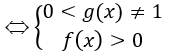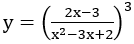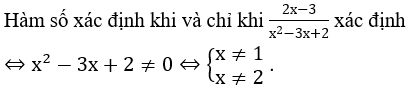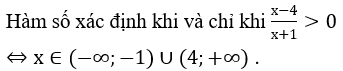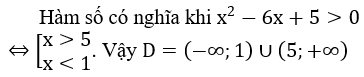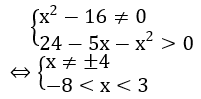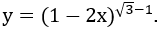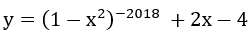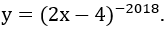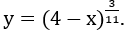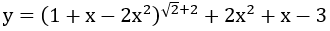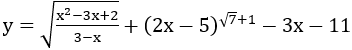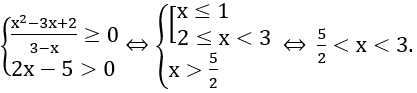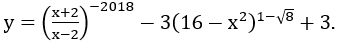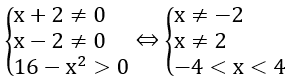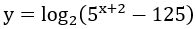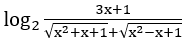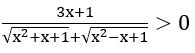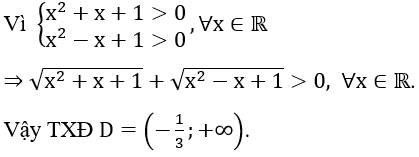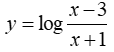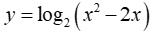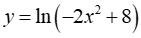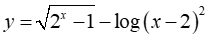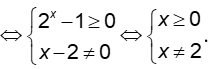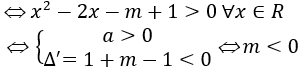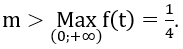Tìm tập xác định của hàm số mũ, lũy thừa, lôgarit mới nhất 2024

Phương pháp giải 

Bài toán 1: Tập xác định của hàm lũy thừa, hàm vô tỷ

Xét hàm số y = [f(x)]^α

    • Khi α nguyên dương: hàm số xác định khi và chỉ khi f(x) xác định.

    • Khi α nguyên âm: hàm số xác định khi và chỉ khi f(x) ≠ 0.

    • Khi α không nguyên: hàm số xác định khi và chỉ khi f(x) > 0.

Bài toán 2: Tập xác định của hàm số logarit

    • Hàm số y = log_af(x) xác định 

    • Hàm số y = log_g(x)f(x) xác định 

    • Hàm số y = (f(x))^g(x) xác định ⇔ f(x) > 0

Ví dụ minh họa

Bài 1: Tìm tập xác định D của hàm số y=(x²-1)^-8

Lời giải:

Hàm số xác định khi và chỉ khi x²-1 ≠ 0 ⇔ x ≠ ±1

Bài 2: Tìm tập xác định của hàm số

Lời giải:

Bài 3: Tìm tập xác định của hàm số

Lời giải:

Bài 4: Tìm tập xác định D của hàm số y=log(x²-6x+5)

Lời giải:

Bài 5: Tìm tập xác định của hàm số y=(x²-16)^-5-ln(24-5x-x²).

Lời giải:

Tập xác định của hàm số y = (x²-16)^-5 - ln(24-5x-x²)là:

Vậy tập xác định là : D=(-8;3)\{-4}.

Bài tập vận dụng

Bài 1: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi 1-2x > 0 ⇔ x < 1/2

Bài 2: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi 1-x² ≠ 0 ⇔ x ≠ ±1

Bài 3: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi 2x-4 ≠ 0 ⇔ x ≠ 2

Bài 4: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi 4-x > 0 ⇔ x < 4

Bài 5: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi 1+x-2x² > 0 ⇔ -1/2 < x < 1

Bài 6: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi

Vậy tập xác định của hàm số là D=(5/2; 3).

Bài 7: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi

Vậy tập xác định của hàm số là D=(-4 ; 4)\{-2 ,2}.

Bài 8: Tìm tập xác định của hàm số

Lời giải:

Hàm số xác định khi 5^x+2-125 > 0 ⇔ 5^x+2 > 5³ ⇔ x > 1.

Vậy tập xác định D=(1;+∞).

Bài 9: Tìm tập xác định của hàm số

Lời giải:

Hàm số có nghĩa khi

⇔ 3x+1 > 0 ⇔ x > -1/3.

Bài 10: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi và chỉ khi

Bài 11: Tìm tập xác định D của hàm số

Lời giải:

Hàm số xác định khi x² - 2x > 0 ⇔ x < 0 ∪ x > 2

Vậy tập xác định của hàm số là D = (-∞ 0) ∪ (2; +∞)

Bài 12: Tìm tập xác định D của hàm số

Lời giải:

Ta có hàm số xác định khi -2x² + 8 > 0 ⇔ -2 < x < 2

Bài 13: Tìm tập xác định của hàm số

Lời giải:

Hàm số đã cho xác định

Vậy tập xác định của hàm số là D = [0; +∞]\{2}

Bài 14: Tìm tất cả các giá trị thực của tham số m để hàm sốy=log⁡(x²-2x-m+1) có tập xác định là R.

Lời giải:

Để hàm số y=log⁡(x²-2x-m+1) có tập xác định là R

Bài 15: Tìm tập hợp tất cả các giá trị của tham số m để hàm số y=log₂(4^x-2^x+m) có tập xác định D=R.

Lời giải:

Hàm số có tập xác định D = R khi 4^x - 2^x + m > 0, (1), ∀x ∈ R

Đặt t = 2^x, t > 0

Khi đó (1) trở thành t² - t + m > 0 ⇔ m > -t²+t, ∀ t ∈ (0;+∞)

Đặt f(t) = -t² + t

Lập bảng biến thiên của hàm f(t) = -t² + t trên khoảng (0;+∞)

Yêu cầu bài toán xảy ra khi

Xem thêm các dạng bài tập Toán chi tiết và hay khác:

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2023)

60 Bài tập về Lôgarit (có đáp án năm 2023)

60 Bài tập về Phương trình mũ và phương trình logarit (có đáp án năm 2023)

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (có đáp án năm 2023)

60 Bài tập về Nguyên hàm ( có đáp án năm 2023 )