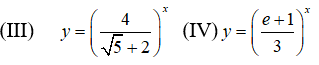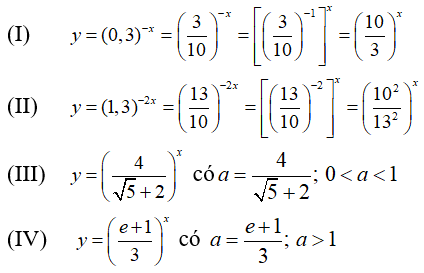30 Bài tập về đồ thị hàm số mũ
I. Phương pháp giải
1. Hàm số mũ:
Cho số thực dương a khác 1. Hàm số y=ax được gọi là hàm số mũ cơ số a.
* Đạo hàm của hàm số mũ
Định lí 1:
Hàm số y=ex có đạo hàm tại mọi x và (ex)′=ex.
Định lí 2:
Hàm số y=ax(a>0,a≠1) có đạo hàm tại mọi x và (ax)′=axlna.
* Khảo sát hàm số mũ y=ax(a>0,a≠1)
1. y=ax,a>1
- Tập xác định: R
- Sự biến thiên:
y=axlna>0,∀x
Giới hạn đặc biệt:
Tiệm cận:
Trục Ox là tiệm cận ngang.
- Bảng biến thiên: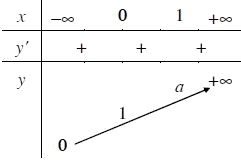
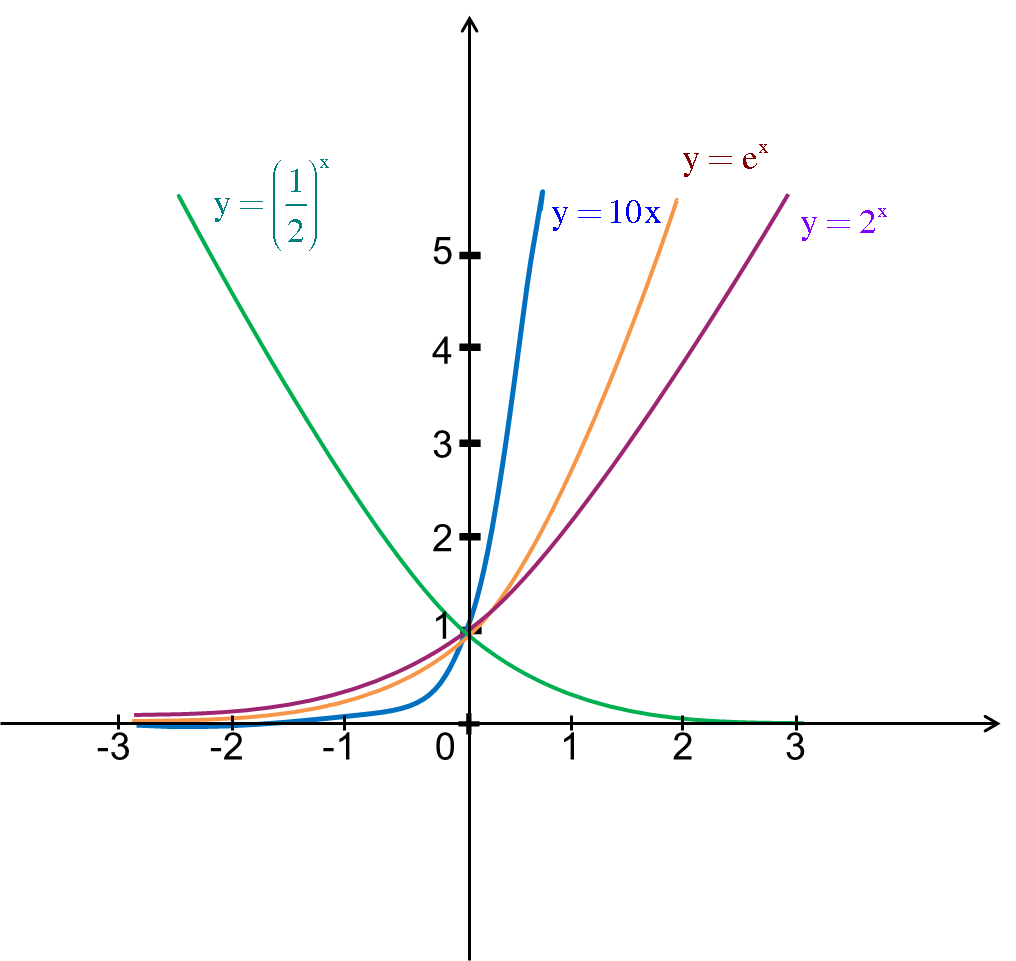
- Đồ thị (Hình 06)
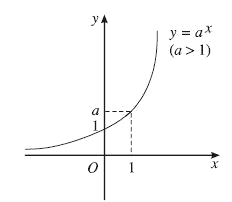
Hình 06
2.
- Tập xác định:
- Sự biến thiên:
Giới hạn đặc biệt:
Tiệm cận:
Trục Ox là tiệm cận ngang.
- Bảng biến thiên:

- Đồ thị (Hình 07)
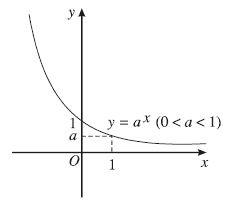
Hình 07
Bảng tóm tắt các tính chất của hàm số mũ

2. Các bước vẽ đồ thị hàm số mũ
Bước 1: Khảo sát hàm số mũ.
Bước 2: Xác định tiệm cận bằng cách lập bảng biến thiên.
Bước 3: Vẽ đồ thị.
Các bạn cần lưu ý cơ số a để xác định hàm số nghịch biến hay đồng biến và chiều của đồ thị.
Để có thể hiểu rõ, mời các bạn theo dõi ví dụ sau đây:
Ví dụ: Hãy vẽ đồ thị hàm số của y=(3/2)x

3. Các dạng toán về hàm số mũ:
Dạng 1: Tìm hàm số có đồ thị cho trước và ngược lại.
Phương pháp:
- Bước 1: Quan sát dáng đồ thị, tính đơn điệu,…của các đồ thị bài cho.
- Bước 2: Đối chiếu với hàm số bài cho và chọn kết luận.
Dạng 2: Tìm mối quan hệ giữa các cơ số khi biết đồ thị.
Phương pháp:
- Bước 1: Quan sát các đồ thị, nhận xét về tính đơn điệu để nhận xét các cơ số.
+ Hàm số đồng biến thì cơ số lớn hơn .
+ Hàm số nghịch biến thì cơ số lớn hơn và nhỏ hơn .
- Bước 2: So sánh các cơ số dựa vào phần đồ thị của hàm số.
- Bước 3: Kết hợp các điều kiện ở trên ta được mối quan hệ cần tìm.
Dạng 3: Tính đạo hàm các hàm số.
Phương pháp:
- Bước 1: Áp dụng các công thức tính đạo hàm của tổng, hiệu, tích, thương để tính đạo hàm hàm số đã cho.
- Bước 2: Tính đạo hàm các hàm số thành phần dựa vào công thức tính đạo hàm các hàm số cơ bản: hàm đa thức, phân thức, hàm mũ, logarit, lũy thừa,…
- Bước 3: Tính toán và kết luận.
Dạng 4: Tính giới hạn các hàm số.
Phương pháp:
Áp dụng các công thức tính giới hạn đặc biệt để tính toán:
; ; ; .
Dạng 5: Tìm GTLN, GTNN của hàm số mũ trên một đoạn.
Phương pháp:
- Bước 1: Tính , tìm các nghiệm của phương trình .
- Bước 2: Tính .
- Bước 3: So sánh các giá trị vừa tính ở trên và kết luận GTLN, GTNN của hàm số.
+ GTNN là số nhỏ nhất trong các giá trị tính được.
+ GTLN là số lớn nhất trong các giá trị tính được.
II. Bài tập vận dụng
Bài 1: Cho các hàm số:
(I) y = (0,3)-x (II) y = (1,3)-2x
Trong các hàm số đã cho, hàm số nào đồng biến trên R ?
Lời giải:
Hàm số đồng biến khi a > 1.
Viết lại các hàm số về dạng hàm số mũ y = ax :
Trong bốn cơ số ta thấy chỉ có hai cơ số lớn hơn 1 là
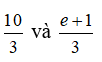
Do đó chỉ có hai hàm số (I) và (IV) là đồng biến trên R
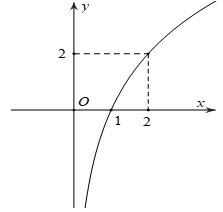
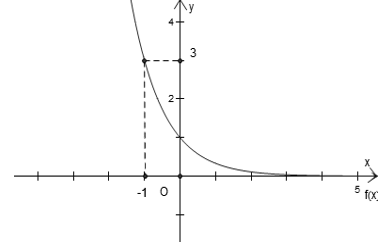
Bài 2: Tìm a để hàm số y=logax (0 < a ≠ 1) có đồ thị là hình bên dưới:
A. a=1/√2
B. a=-1/√2
C. a=1/2
D. a=√2
Lời giải:
Đáp án : D
Giải thích :
Đồ thị hàm số đi qua A(2;2) ⇒ 2=loga2 ⇒ a2=2 ⇒ a=√2 .
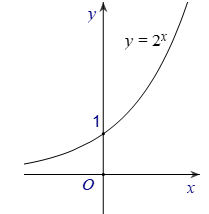
Bài 3: Biết hàm số y=2x có đồ thị là hình bên.
Khi đó, hàm số y=2|x| có đồ thị là hình nào trong bốn hình được liệt kê ở bốn A, B, C, D dưới đây ?
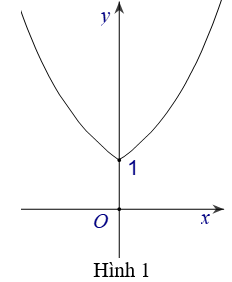
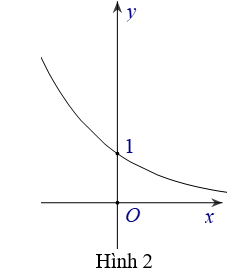
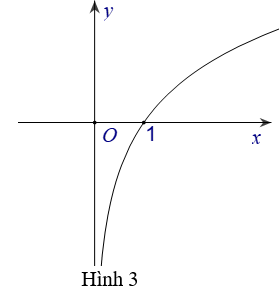
A. Hình 3
B. Hình 2
C. Hình 1
D. Hình 4
Lời giải:
Đáp án : A
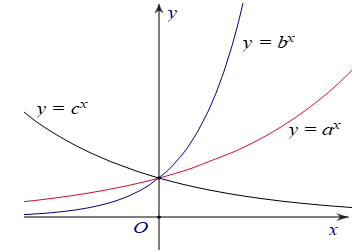
Bài 4: Hình bên là đồ thị của ba hàm số y=ax, y=bx, y=cx được vẽ trên cùng một hệ trục tọa độ. Khẳng định nào sau đây là khẳng định đúng?
A. c > b > a
B. a > b > c
C. a > c > b
D. b > a > c
Lời giải:
Đáp án : D
Giải thích :
Do y=ax và y=bx là hai hàm đồng biến nên a, b > 1
Do y=cx nghịch biến nên c < 1. Vậy x bé nhất.
Mặt khác: Lấy x=m, khi đó tồn tại y1, y2 > 0
Dễ thấy
Vậy b > a > c
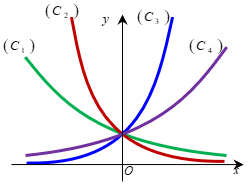
Bài 5: Cho bốn hàm số y=(√3)x (1),y=(1/√3)x (2),y=4x (3),y=(1/4)x (4) và bốn đường cong(C1),(C2),(C2),(C4) như hình vẽ bên. Đồ thị các hàm số (1), (2), (3), (4) lần lượt là:
A. (C2), (C3), (C4), (C1)
B. (C1), (C2), (C3), (C4)
C. (C4), (C1), (C3), (C2)
D. (C1), (C2), (C4), (C3)
Lời giải:
Đáp án : C
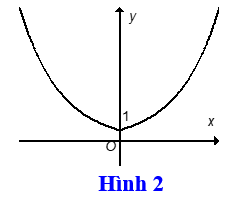
Bài 6: Cho hàm số y=(√2)x có đồ thị Hình 1 . Đồ thị Hình 2 là của hàm số nào dưới đây?
A. y=|(√2)x |
B. y=-(√2)x
C. y=(√2)|x|
D. y= -|(√2)x |
Lời giải:
Đáp án : C
Bài 7:Trong các hàm số sau đây, hàm số nào là hàm số mũ ? Với cơ số bao nhiêu ?
Lời giải chi tiết
Các hàm số mũ là với cơ số là ; với cơ số là ; với cơ số là
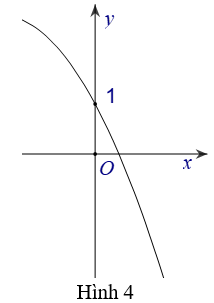
Bài 8: Hàm số nào có đồ thị như hình vẽ bên?
A. y=(1/3)x
B. y=(1/√2)x
C. y=3x
D. y=(√2)x
Lời giải: Đáp án : A
Bài 9: Cho bốn hàm số y=(√3)x (1),y=(1/√3)x (2),y=4x (3),y=(1/4)x (4) và bốn đường cong(C1),(C2),(C2),(C4) như hình vẽ bên. Đồ thị các hàm số (1), (2), (3), (4) lần lượt là:
A. (C2), (C3), (C4), (C1)
B. (C1), (C2), (C3), (C4)
C. (C4), (C1), (C3), (C2)
D. (C1), (C2), (C4), (C3)
Lời giải: Đáp án : CXem thêm các dạng bài tập hay, có đáp án:
30 Bài tập về Cách tìm nguyên hàm của hàm số mũ, hàm số logarit (2024) cực hay, có đáp án