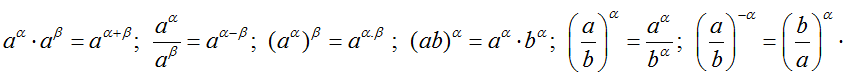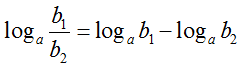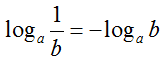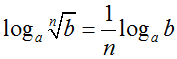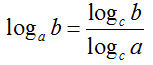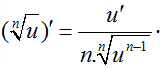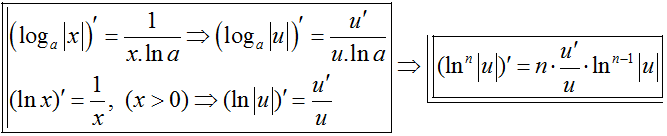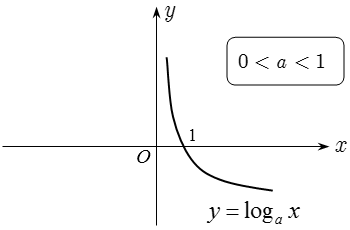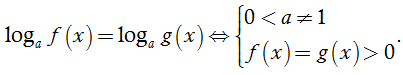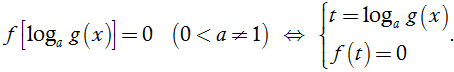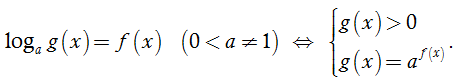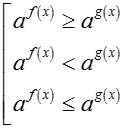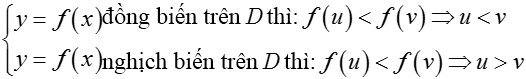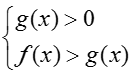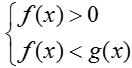30 bài tập về biến thiên hàm số mũ, hàm số lũy thừa, logarit 2024 (có đáp án)

Bài tập về biến thiên hàm số mũ, hàm số lũy thừa, logarit

I. Lý thuyết

** LŨY THỪA

1. Định nghĩa lũy thừa và căn

    • Cho số thực b và số nguyên dương n (n ≥ 2) . Số a được gọi là căn bậc n của số b nếu aⁿ = b .

    • Chú ý: - Với n lẻ và b ∈ R : Có duy nhất một căn bậc n của b, kí hiệu là ⁿ√b .

    - Với n chắn:

        +) b < 0: Không tồn tại căn bậc n của b.

        +) b = 0: Có một căn bậc n của b là số 0.

        +) b > 0: Có hai căn bậc n của a là hai số đối nhau, căn có giá trị dương ký hiệu là ⁿ√b, căn có giá trị âm kí hiệu là -ⁿ√b.

Số mũ α	Cơ số a	Lũy thừa aα
α = n ∈ N*	a ∈ R	aα = an = a.a. ... .a (n thừa số a)
α = 0	a ≠ 0	aα = a0 = 1
α = -n (n ∈ N*)	a ≠ 0	aα = a0 = 1/an
α = m/n	a > 0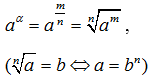
α = lim rn (rn ∈ Q, n ∈ N*)	a > 0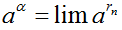

2. Một số tính chất của lũy thừa

    • Giả thuyết rằng mỗi biểu thức được xét đều có nghĩa:

    • Nếu a > 1 thì a^α > a^β ⇔ α > β ; Nếu ) < a < 1 thì a^α > a^β ⇔ α < β .

    • Với mọi 0 < a < b, ta có: a^m < b^m ⇔ m > 0; a^m > b^m ⇔ m < 0 ;

    • Chú ý: - Các tính chất trên đúng trong trường hợp số mũ nguyên hoặc không nguyên.

    - Khi xét lũy thừa với số mũ 0 và số mũ nguyên âm thì cơ số a phải khác 0.

    - Khi xét lũy thừa với số mũ không nguyên thì cơ số a phải dương.

** HÀM SỐ LŨY THỪA

1. Định nghĩa: Hàm số y = x^α với α ∈ R được gọi là hàm số lũy thừa.

2. Tập xác định: Tập xác định của hàm số y = x^α là:

    • D = R nếu α là số nguyên dương.

    • D = R \ {0} với α nguyên âm hoặc bằng 0

    • D = (0; +∝) với α không nguyên.

3. Đạo hàm: Hàm số y = x^α có đạo hàm với mọi x > 0 và (x^α)' = α.x^{α - 1}.

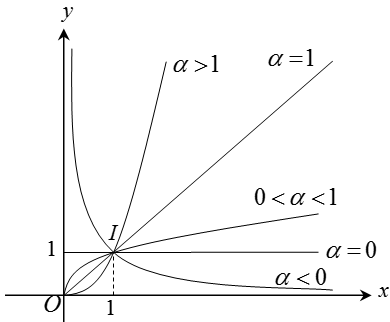
4. Tính chất của hàm số lũy thừa trên khoảng (0; +∝).

y = xα, α > 0	y = xα, α < 0
a. Tập khảo sát: (0; +∝)	a. Tập khảo sát: (0; +∝)
b. Sự biến thiên + y' = αxα - 1 > 0, ∀x > 0 + Giới hạn đặc biệt + Tiệm cận: không có	b. Sự biến thiên + y' = αxα - 1 < 0, ∀x > 0 + Giới hạn đặc biệt + Tiệm cận: không có - Trục 0x là tiệm cận ngang - Trục 0y là tiệm cận đứng.
c. Bảng biến thiên	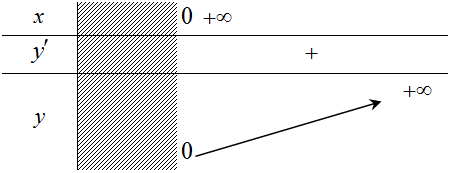c. Bảng biến thiên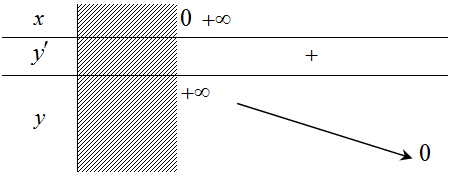

    d. Đồ thị:

    Đồ thị của hàm số lũy thừa y = x^α luôn đi qua điểm I(1; 1)

    Lưu ý: Khi khảo sát hàm số lũy thừa với số mũ cụ thể, ta phải xét hàm số đó trên toàn bộ tập xác định của nó. Chẳng hạn: y = x³, y = x^-2, y = x^π

** LÔGARIT

1. Định nghĩa:

    Cho hai số dương a, b với a ≠ 1 . Số α thỏa mãn đẳng thức a^α = b được gọi là lôgarit cơ số a của b và kí hiệu là log_ab. Ta viết: α = log_ab ⇔ a^α = b.

2. Các tính chất: Cho a, b > 0, a ≠ 1 ta có:

    - log_aa = 1, log_a1 = 0

    - a^log_ab = b, log_a(a^α) = α

3. Lôgarit của một tích: Cho 3 số dương a, b₁, b₂ với a ≠ 1 , ta có

    - log_a(b₁.b₂) = log_ab₁ + log_ab₂

4. Lôgarit của một thương: Cho 3 số dương a, b₁, b₂ với a ≠ 1, ta có

    - 

    - Đặc biệt : với a, b > 0, a ≠ 1 

5. Lôgarit của lũy thừa: Cho a, b₁, b₂, a ≠ 1, với mọi α, ta có

    - log_ab^α = αlog_ab

    - Đặc biệt: 

6. Công thức đổi cơ số: Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1 , ta có

    - 

    - Đặc biệt : 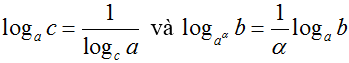 với α ≠ 0 .

        + Lôgarit thập phân và Lôgarit tự nhiên

        + Lôgarit thập phân là lôgarit cơ số 10. Viết: log₁₀b = log b = lg b

        + Lôgarit tự nhiên là lôgarit cơ số e. Viết: log_eb = ln b

** HÀM SỐ MŨ. HÀM SỐ LÔGARIT

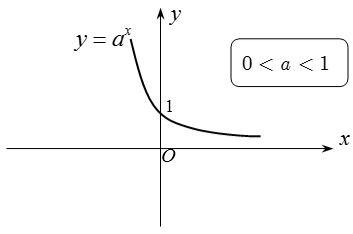
1. Hàm số mũ: y = a^x, (a > 0, a ≠ 1)

    1.1 Tập xác định: D = R

    1.2. Tập giá trị: T = (); +∝), nghĩa là khi giải phương trình mũ mà đặt t = a^f(x) thì t > 0

    1.3. Tính đơn điệu:

        + Khi a > 1 thì hàm số y = a^x đồng biến, khi đó ta luôn có: a^f(x) > a^g(x) ⇔ f(x) > g(x).

        + Khi 0 < a < 1 thì hàm số y = a^x nghịch biến, khi đó ta luôn có: a^f(x) > a^g(x) ⇔ f(x) < g(x).

    1.4. Đạo hàm:

    (a^x)' = a^x.ln a ⇒ (a^u)' = u'.a^u.ln a

    (e^x)' = e^x ⇒ (e^u)' = e^u.u'

    1.5. Đồ thị: Nhận trục hoành làm đường tiệm cận ngang.

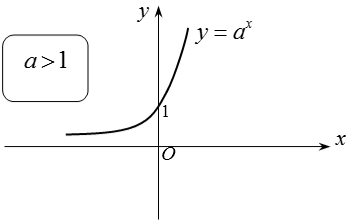
2. Hàm số logarit: y = log_ax, (a > 0, a ≠ 1)

    2.1 Tập xác định: D = (0; +∝)

    2.2. Tập giá trị: T = R, nghĩa là khi giải phương trình logarit mà đặt t = log_ax thì t không có điều kiện.

    2.3. Tính đơn điệu:

        + Khi a > 1 thì y = log_ax đồng biến trên D khi đó nếu: log_af(x) > log_ag(x) ⇔ f(x) > g(x).

        + Khi 0 < a < 1 thì y = log_ax nghịch biến trên D khi đó nếu log_af(x) > log_ag(x) ⇔ f(x) < g(x).

    2.4 Đạo hàm:

    2.5. Đồ thị: Nhận trục tung làm đường tiệm cận đứng.

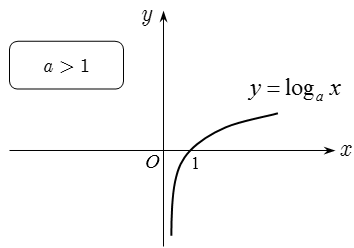
** PHƯƠNG TRÌNH MŨ VÀ PHƯƠNG TRÌNH LÔGARIT

1. PHƯƠNG TRÌNH MŨ.

1.1. Phương trình mũ cơ bản a^x = b (a > 0, a ≠ 1).

    ● Phương trình có một nghiệm duy nhất khi b > 0 .

    ● Phương trình vô nghiệm khi b ≤ 0 .

1.2. Biến đổi, quy về cùng cơ số

    a^f(x) = a^g(x) ⇔ a = 1 hoặc  .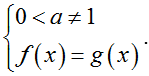

1.3. Đặt ẩn phụ

    f[a^g(x)] = 0 ( 0 < a ≠ 1) ⇔ .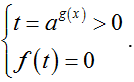

    Ta thường gặp các dạng:

    ● m.a^2f(x) + n.a^f(x) + p = 0

    ● m.a^f(x) + n.b^f(x) + p = 0, trong đó a.b = 1. Đặt t = a^f(x). t > 0, suy ra b^f(x) = 1/t.

    ● m.a^2f(x) + n.(a.b)^f(x) + p.b^2f(x) = 0. Chia hai vế cho b^2f(x) và đặt (a/b)^f(x) = t > 0.

1.4. Logarit hóa

    ● Phương trình  .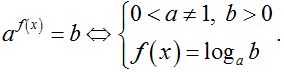

    ● Phương trình a^f(x) = b^g(x) ⇔ log_aa^f(x) = log_ab^g(x) ⇔ f(x) = g(x).log_ab

    hoặc log_ba^f(x) = log_bb^g(x) ⇔ f(x).log_ba = g(x)

1.5. Giải bằng phương pháp đồ thị

    o Giải phương trình: a^x = f(x) (0 < a ≠ 1) (*) .

    o Xem phương trình (*) là phương trình hoành độ giao điểm của hai đồ thị y = a^x (0 < a ≠ 1) và y = f(x) . Khi đó ta thực hiện hai bước:

    - Bước 1. Vẽ đồ thị các hàm số y = a^x (0 < a ≠ 1) và y = f(x) .

    - Bước 2. Kết luận nghiệm của phương trình đã cho là số giao điểm của hai đồ thị.

1.6. Sử dụng tính đơn điệu của hàm số

    o Tính chất 1. Nếu hàm số y = f(x) luôn đồng biến (hoặc luôn nghịch biến) trên (a; b) thì số nghiệm của phương trình f(x) = k trên (a; b) không nhiều hơn một và f(u) = f(v) ⇔ u = v, ∀u, v ∈ (a; b).

    o Tính chất 2. Nếu hàm số y = f(x) liên tục và luôn đồng biến (hoặc luôn nghịch biến) ; hàm số y = g(x) liên tục và luôn nghịch biến (hoặc luôn đồng biến) trên D thì số nghiệm trên D của phương trình f(x) = g(x) không nhiều hơn một.

    o Tính chất 3. Nếu hàm số y = f(x) luôn đồng biến (hoặc luôn nghịch biến) trên D thì bất phương trình f(u) > f(v) ⇔ u > v (hoặc u < v), ∀u,v ∈ D.

1.7. Sử dụng đánh giá

    o Giải phương trình f(x) = g(x).

    o Nếu ta đánh giá được .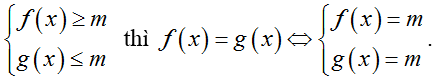

2. PHƯƠNG TRÌNH LÔGARIT

2.1. Biến đổi, quy về cùng cơ số

2.2. Đặt ẩn phụ

2.3. Mũ hóa hai vế

2.4. Phương pháp đồ thị

2.5. Sử dụng tính đơn điệu của hàm số

** BẤT PHƯƠNG TRÌNH MŨ VÀ LÔGARIT

1. Bất phương trình mũ:

    • Khi giải bất phương trình mũ, ta cần chú ý đến tính đơn điệu của hàm số mũ.

    . Tương tự với bất phương trình dạng: 

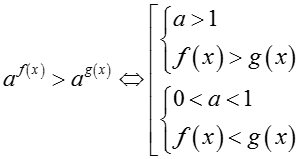
    • Trong trường hợp cơ số a có chứa ẩn số thì: a^M > a^N ⇔ (a - 1)(M - N) > 0 .

    • Ta cũng thường sử dụng các phương pháp giải tương tự như đối với phương trình mũ:

        + Đưa về cùng cơ số.

        + Đặt ẩn phụ.

 + Sử dụng tính đơn điệu 

2. Bất phương trình lôgarit:

    • Bất phương trình lôgarit cơ bản có dạng: log_af(x) > b; log_af(x) ≥ b; log_af(x) < b; log_af(x) ≤ b

    Phương pháp giải bất phương trình lôgarit

    • Đưa về cùng cơ số

    - Nếu a > 1 thì log_af(x) > log_ag(x) ⇔ 

    - Nếu 0 < a < 1 thì log_af(x) > log_ag(x) ⇔ 

    • Đặt ẩn phụ

    • Mũ hóa

II. Ví dụ minh họa

 Ví dụ 1. Hàm số $y={\left(x-2\right)}^{\frac{1}{2}}$ có tập xác định là

A. $D=\left[2;+\infty \right)$

B. $D=ℝ$

C. $D=\left(2;+\infty \right)$

D. $D=ℝ\backslash \left\{2\right\}$

Lời giải

Chọn C

Vì $\frac{1}{2}$ không nguyên nên hàm số $y={\left(x-2\right)}^{\frac{1}{2}}$ xác định khi $x-2>0\iff x>2$.

Tập xác định của hàm số là $D=\left(2;+\infty \right)$.

Ví dụ 2.Cho hàm số $y=x^{-4}$. Tìm mệnh đề sai trong các mệnh đề sau.

A. Đồ thị hàm số có một trục đối xứng.

B. Đồ thị hàm số đi qua điểm(1,1).

C. Đồ thị hàm số có hai đường tiệm cận.

D. Đồ thị hàm số có một tâm đối xứng.

Lời giải

Chọn D

* TXĐ: $D=ℝ\backslash \left\{0\right\}$.

Ta có: $y=x^{-4}=\frac{1}{x^4}$$\forall x\in D\Rightarrow -x\in D$ và $y\left(-x\right)=\frac{1}{{\left(-x\right)}^4}=\frac{1}{x^4}=y\left(x\right)$ nên hàm số đã cho là hàm số chẵn $\Rightarrow$Đồ thị hàm số nhận trục Oy làm trục đối xứng $\Rightarrow$A đúng.

* Đồ thị hàm số đi qua điểm (1;1) nên B đúng.

* Ta có: $\underset{x\to \pm \infty }{\lim }y=0\Rightarrow$TCN: y = 0;$\underset{x\to 0^{+}}{\lim }y=+\infty \Rightarrow$ TCĐ: x = 0.

Đồ thị hàm số có hai đường tiệm cận nên C đúng.

III. Bài tập vận dụng

Câu 1. Tập xác định của hàm số $y={\left(x^2-5x+6\right)}^{-2019}$ là

A. $\left(-\infty ;2\right)\cup \left(3;+\infty \right)$

B.(2;3).

C. $R\backslash \left\{2;3\right\}$

D. $\left(-\infty ;2\right]\cup \left[3;+\infty \right)$

Lời giải

Chọn C

Vì -2019 là số nguyên âm nên hàm số $y={\left(x^2-5x+6\right)}^{-2019}$ xác định khi :

$x^2-5x+6\ne 0\iff \left\{\begin{array}{l}x\ne 2\\ x\ne 3\end{array}\right.$

Câu 2.Tìm tập xác định của hàm số $y={\left(x^2-x-2\right)}^{\sqrt{2}}$.

A. $D=ℝ$

B. $D=\left(-\infty ;-1\right]\cup \left[2;+\infty \right)$

C. $D=\left(-\infty ;-1\right)\cup \left(2;+\infty \right)$

D. $D=ℝ\backslash \left\{-1;2\right\}$

Lời giải

Chọn C

Vì $\sqrt{2}$ không nguyên nên hàm số $y={\left(x^2-x-2\right)}^{\sqrt{2}}$ xác định khi:

$x^2-x-2>0\iff \left[\begin{array}{l}x<-1\\ x>2\end{array}\right.$

TXĐ: $D=\left(-\infty ;-1\right)\cup \left(2;+\infty \right)$

Câu 3. Tập xác định của hàm số $y={\left(x^3-27\right)}^{\frac{\pi }{2}}$ là

A. $D=\left(3;+\infty \right)$

B. $D=ℝ\backslash \left\{2\right\}$

C. $ℝ$

D. $D=\left[3;+\infty \right)$

Lời giải

Chọn A

Vì $\frac{\pi }{2}$ không nguyên nên hàm số đã cho xác định khi :

$$\begin{gathered} x^3-27>0 \\ \iff x^3>27\iff x>3 \end{gathered}$$

Câu 4. Có bao nhiêu giá trị nguyên của $m\in \left(-2018;2018\right)$ để hàm số $y={\left(x^2-2x-m+1\right)}^{\sqrt{2018}}$ có tập xác định là $D=ℝ$

A. 2017.

B. Vô số.

C. 2018.

D. 2016.

Lời giải

Chọn A

Vì $\sqrt{2018}$ không nguyên nên hàm số $y={\left(x^2-2x-m+1\right)}^{\sqrt{2018}}$ có tập xác định là D khi và chỉ khi $x^2-2x-m+1>0$,

$\forall x\in ℝ\iff x^2-2x+1>m$,

$\forall x\in ℝ\iff {\left(x-1\right)}^2>m$,

$\forall x\in ℝ\iff m<0$.

$$\begin{gathered} m\in \left(-2018;2018\right) \\ \Rightarrow m\in \left(-2018;0\right) \end{gathered}$$

mà m nguyên nên $m\in \left\{-2017;-2016;\mathrm{...};-1\right\}$.Vậy có 2017 giá trị nguyên của m.

Câu 5: Tìm tập xác định D của hàm số $y={\log }_3\left(2x+1\right)$.

A. $D=\left(-\infty ;-\frac{1}{2}\right)$

B. $D=\left(\frac{1}{2};+\infty \right)$

C. $D=\left(0;+\infty \right)$

D. $D=\left(-\frac{1}{2};+\infty \right)$

Lời giải

Chọn D

Hàm số $y={\log }_3\left(2x+1\right)$ có nghĩa khi $2x+1>0\iff x>-\frac{1}{2}$. Vậy TXĐ là $D=\left(-\frac{1}{2};+\infty \right)$

Câu 6: Tìm tập xác định D của hàm số $y={\log }_3\left(x^2+3x+2\right)$

A. D = [-2, -1].

B. $D=\left(-\infty ;-2\right)\cup \left(-1;+\infty \right)$

C. D = (-2, -1).

D. $D=\left(-\infty ;-2\right]\cup \left[-1;+\infty \right)$

Lời giải

Chọn B

Điều kiện $x^2+3x+2>0\iff \left[\begin{array}{l}x<-2\\ x>-1\end{array}\right.$. Vậy tập xác định của hàm số $y={\log }_3\left(x^2+3x+2\right)$ là: $D=\left(-\infty ;-2\right)\cup \left(-1;+\infty \right)$

Câu 7: Hàm số $y={\log }_2\left(-x^2+5x-6\right)$ có tập xác định là:

A. (2, 3).

B. $\left(-\infty ;2\right)\cup \left(3;+\infty \right)$

C. $\left(-\infty ;2\right)$

D. $\left(3;+\infty \right)$

Lời giải

Chọn A

Hàm số có nghĩa khi và chỉ khi $-x^2+5x-6>0\iff$ 2 < x < 3.

Kết luận. Vậy tập xác định là (2; 3).

Câu 8: Tập xác định của hàm số $y=\ln \left(x-1\right)+\ln \left(x+1\right)$ là:

A. $\left(1;+\infty \right)$

B. $\left(-\infty ;\sqrt{2}\right)$

C. $\varnothing$

D. $\left[\sqrt{2};+\infty \right)$

Lời giải

Chọn A

Ta có:

$$\begin{gathered} \left\{\begin{array}{l}x-1>0\\ x+1>0\end{array}\right. \\ \iff \left\{\begin{array}{l}x>1\\ x>-1\end{array}\right.\iff x>1 \end{gathered}$$

Kết luận: Vậy tập xác định $D=\left(1;+\infty \right)$.

Câu 9: Cho hàm số $y={\left(\frac{3}{4}\right)}^{x^2-2x+2}$. Trong các khẳng định dưới đây, khẳng định nào đúng?

A. Hàm số luôn đồng biến trên R.

B. Hàm số luôn nghịch biến trên khoảng $\left(-\infty ;1\right)$.

C. Hàm số luôn đồng biến trên trên $\left(-\infty ;1\right)$.

D. Hàm số luôn nghịch biến trên R.

Lời giải

Chọn C

$y^{\text{'}}=\left(2x-2\right){\left(\frac{3}{4}\right)}^{x^2-2x+2}\ln \frac{3}{4}$

$y^{\text{'}}=0\iff x=1$

Bảng biến thiên:

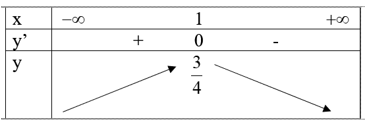
Từ bảng biến thiên ta có hàm số luôn đồng biến trên trên $\left(-\infty ;1\right)$.

Câu 10: Hàm số nào sau đây nghịch biến trên tập xác định của nó?

A. $y={\log }_{\frac{\text{e}}{\pi }}x$

B. $y={\log }_{\sqrt{3}}x$

C. $y={\log }_{2}x$

D. $y={\log }_{\pi }x$

Lời giải

Chọn A

Xét hàm $y={\log }_{\frac{\text{e}}{\pi }}x$ có TXĐ: $D=\left(0;+\infty \right)$

Vì $0<\frac{e}{\pi }<1$ nên $y={\log }_{\frac{\text{e}}{\pi }}x$ là hàm nghịch biến trên tập xác định D.

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

60 Bài tập về Hàm số mũ, Hàm số logarit (2024) có đáp án 

60 Bài tập về Bất phương trình mũ và bất phương trình logarit (2024) có đáp án 

60 Bài tập về Hàm số lũy thừa (có đáp án năm 2024) - 

60 Bài tập về Lôgarit (có đáp án năm 2024) 

60 Bài tập về Phương trình mũ và phương trình logarit (có đáp án năm 2024)