30 bài tập các công thức đạo hàm của logarit 2024 (có đáp án)

Bài tập về các công thức đạo hàm của logarit

I. Lý thuyết

1. Định nghĩa

Hiểu một cách đơn giản, hàm logarit là một hàm số được biểu diễn dưới dạng logarit. Cụ thể, với số thực a cho trước (a>0; a≠1; x>0), ta có hàm số y=logax được định nghĩa là hàm số logarit cơ số a. Từ đây, đạo hàm hàm số logarit trên có công thức y’=$\frac{1}{x.\ln a}$

2.Tính chất đạo hàm logarit

Đây là các tính chất của đạo hàm logarit cơ bản được áp dụng nhiều trong các dạng bài khác nhau. Học sinh chú ý ghi nhớ để tính thành thạo đạo hàm log.

3. Bảng đạo hàm logarit đầy đủ và chi tiết nhất

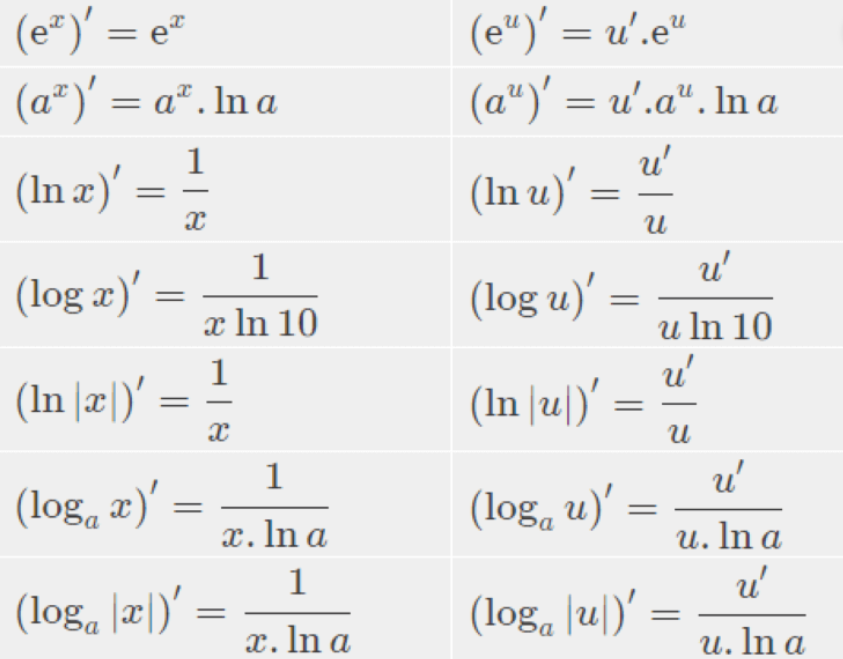
II. Ví dụ minh họa

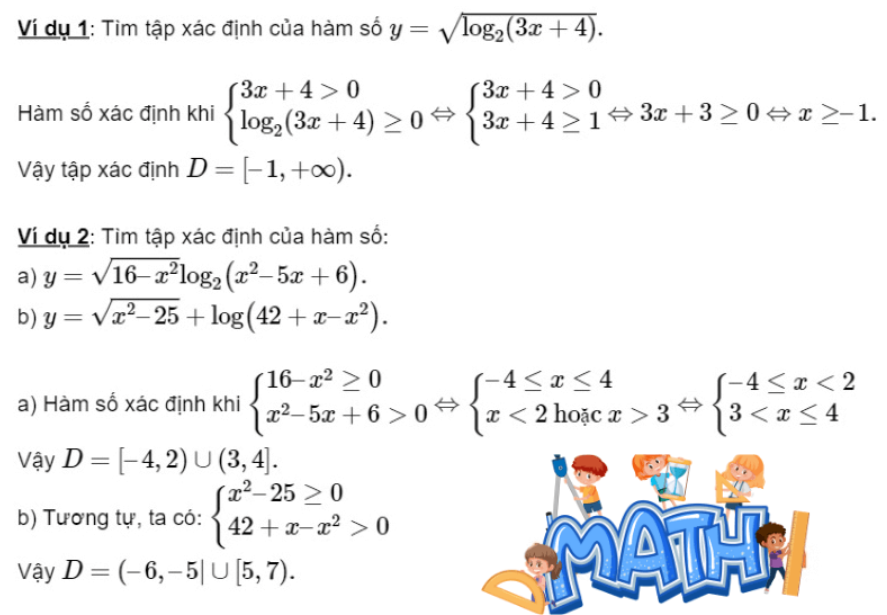
III. Bài tập vận dụng

Câu 1. Trên khoảng $\left(0;+\mathrm{\infty }\right)$, đạo hàm của hàm số $y=lo{g}_{2}x$ là:
A. $y^{\prime }=\frac{1}{xln2}$.
B. $y^{\prime }=\frac{ln2}{x}$.
C. $y^{\prime }=\frac{1}{x}$.
D. $y^{\prime }=\frac{1}{2x}$.

Lời giải

Chọn A.

Ta có: ${\left(lo{g}_{2}x\right)}^{\prime }=\frac{1}{xln2}$.

Câu 2. Tìm đạo hàm của hàm số $y=logx$.
A. $y^{\prime }=\frac{ln10}{x}$
B. $y^{\prime }=\frac{1}{xln10}$
C. $y^{\prime }=\frac{1}{10lnx}$
D. $y^{\prime }=\frac{1}{x}$

Lời giải

Chọn B.

Áp dụng công thức ${\left(lo{g}_{a}x\right)}^{\prime }=\frac{1}{xlna}$, ta được $y^{\prime }=\frac{1}{xln10}$.

Câu 3. Tính đạo hàm của hàm số $y=lo{g}_2\left(2x+1\right)$.
A. $y^{\prime }=\frac{2}{\left(2x+1\right)ln2}$
B. $y^{\prime }=\frac{1}{\left(2x+1\right)ln2}$
C. $y^{\prime }=\frac{2}{2x+1}$
D. $y^{\prime }=\frac{1}{2x+1}$

Lời giải

Chọn A.

Ta có $y^{\prime }={\left(lo{g}_2\left(2x+1\right)\right)}^{\prime }=\frac{{(2x+1)}^{\prime }}{\left(2x+1\right)ln2}=\frac{2}{\left(2x+1\right)ln2}$.

Câu 4. Tính đạo hàm của hàm số $y=log\left(e^x+2\right)$
A. $y^{\prime }=\frac{e^x}{e^x+2}$.
B. $y^{\prime }=\frac{e^x}{\left(e^x+2\right)ln10}$.
C. $y^{\prime }=\frac{1}{e^x+2}$.
D. $y^{\prime }=\frac{1}{\left(e^x+2\right)ln10}$

Lời giải

Chọn B.

$y^{\prime }=\frac{{\left(e^x+2\right)}^{\prime }}{\left(e^x+2\right)ln10}=\frac{e^x}{\left(e^x+2\right)ln10}$.

Câu 5. Tính đạo hàm của hàm số $y=lo{g}_3\left(2x+1\right)$.
A. $y^{\prime }=\frac{1}{\left(2x+1\right)ln3}$.
B. $y^{\prime }=\frac{1}{2x+1}$.
C. $y^{\prime }=\frac{2}{\left(2x+1\right)ln3}$.
D. $y^{\prime }=\left(2x+1\right)\cdot ln3$.

Lời giải

Chọn C

Đạo hàm của hàm số $y=lo{g}_3\left(2x+1\right)$ là $y^{\prime }=\frac{2}{\left(2x+1\right)ln3}$.

Câu 6. Cho hàm số $y=ln\frac{1}{x+1}$. Xác định mệnh đề đúng
A. $x{y}^{\prime }–1=e^y$.
B. $x{y}^{\prime }+1=–e^y$.
C. $x{y}^{\prime }–1=–e^y$.
D. $x{y}^{\prime }+1=e^y$.

Lời giải

Chọn D

Ta có: $y^{\prime }=(–ln\left(x+1\right){)}^{\prime }=–\frac{1}{x+1}\Rightarrow x{y}^{\prime }+1=–\frac{x}{x+1}+1=\frac{1}{x+1}=e^y$.

Câu 7. Hàm số $f\left(x\right)=lo{g}_2\left(x^2–2x\right)$ có đạo hàm
A. $f^{\prime }\left(x\right)=\frac{ln2}{x^2–2x}$
B. $f^{\prime }\left(x\right)=\frac{1}{\left(x^2–2x\right)ln2}$
C. $f^{\prime }\left(x\right)=\frac{\left(2x–2\right)ln2}{x^2–2x}$
D. $f^{\prime }\left(x\right)=\frac{2x–2}{\left(x^2–2x\right)ln2}$

Lời giải

Chọn D.

$f^{\prime }\left(x\right)=\frac{{\left(x^2–2x\right)}^{\prime }}{\left(x^2–2x\right)ln2}=\frac{2x–2}{\left(x^2–2x\right)ln2}$

Câu 8. Tính đạo hàm số $y=f\left(x\right)=lo{g}_{x^2+2}2$.
A. $y^{\prime }=–\frac{2x}{\left(x^2+2\right)\cdot ln2\cdot lo{g}_2^2\left(x^2+2\right)}$.
B. $y^{\prime }=–\frac{1}{lo{g}_2^2\left(x^2+2\right)}$.
C. $y^{\prime }=–\frac{2x}{ln\left(x^2+2\right)}$.
D. $y^{\prime }=–\frac{x}{\left(x^2+2\right)\cdot l{n}^2\left(x^2+2\right)}$.

Lời giải

Chọn A

Ta có: $y=lo{g}_{x^2+2}2=\frac{1}{lo{g}_2\left(x^2+2\right)}\Rightarrow y^{\prime }=–\frac{{\left(lo{g}_2\left(x^2+2\right)\right)}^{\prime }}{lo{g}_2^2\left(x^2+2\right)}=–\frac{2x}{\left(x^2+2\right)\cdot ln2\cdot lo{g}_2^2\left(x^2+2\right)}$.

Câu 9. Đạo hàm của hàm số $y=lo{g}_3\left(x^2+x+1\right)$ là:
A. $y^{\prime }=\frac{\left(2x+1\right)ln3}{x^2+x+1}$
B. $y^{\prime }=\frac{2x+1}{\left(x^2+x+1\right)ln3}$
C. $y^{\prime }=\frac{2x+1}{x^2+x+1}$
D. $y^{\prime }=\frac{1}{\left(x^2+x+1\right)ln3}$

Lời giải

Chọn B.

$y^{\prime }=\frac{{\left(x^2+x+1\right)}^{\prime }}{\left(x^2+x+1\right)ln3}=\frac{2x+1}{\left(x^2+x+1\right)ln3}$

Câu 10. Cho hàm số $f\left(x\right)=lo{g}_2\left(x^2+1\right)$, tính $f^{\prime }\left(1\right)$
A $f^{\prime }\left(1\right)=1$
B. $f^{\prime }\left(1\right)=\frac{1}{2ln2}$.
C. $f^{\prime }\left(1\right)=\frac{1}{2}$.
D. $f^{\prime }\left(1\right)=\frac{1}{ln2}$.

Lời giải

Chọn D.

TXĐ: $D=\mathbb{R}$.

$f^{\prime }\left(x\right)=\frac{2x}{\left(x^2+1\right)\cdot ln2}\Rightarrow f^{\prime }\left(1\right)=\frac{1}{ln2}$.

Xem thêm các dạng câu hỏi và bài tập liên quan khác:

30 bài tập về biến thiên hàm số mũ, hàm số lũy thừa, logarit 2024 (có đáp án) 

30 Bài tập các mẹo tính đạo hàm 2024 (có đáp án) 

Các dạng bài tập về Lôgarit cơ bản (2024) có đáp án 

Tìm tập xác định của hàm số mũ, lũy thừa, lôgarit mới nhất 2024 

20 Bài tập về Giải phương trình logarit chứa tham số (2024) có đáp án