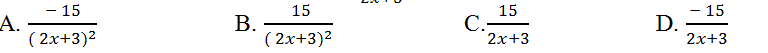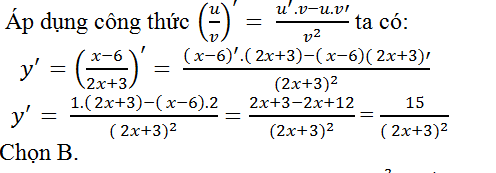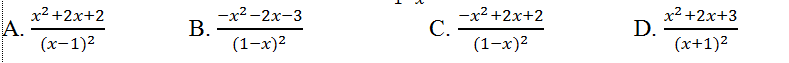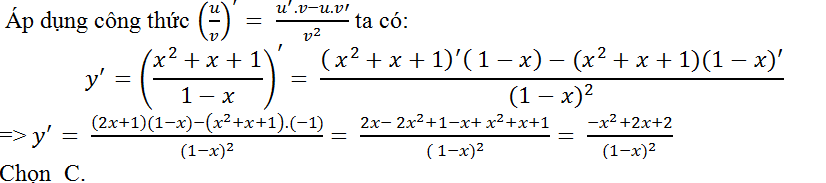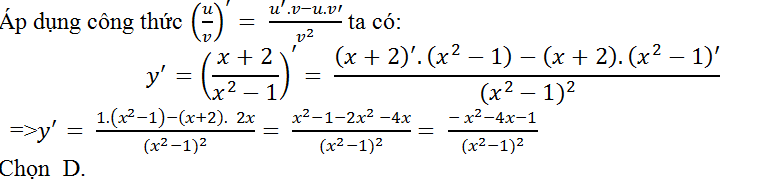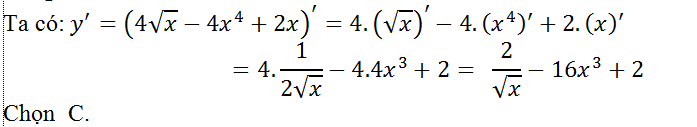30 Bài tập các mẹo tính đạo hàm 2024 (có đáp án)

1900.edu.vn xin giới thiệu bài viết gồm bài tập và phương pháp giải Toán: các mẹo tính đạo hàm hay, chi tiết cùng với bài tập chọn lọc có đáp án giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán 12 . Mời các bạn đón xem.

Bài tập về các mẹo tính đạo hàm

I. Lý thuyết

A. Đạo hàm của hàm phân thức

Để tính đạo hàm phân thức ta sử dụng chung một công thức

$\left( {\frac{u}{v}} \right)' = \frac{{u'.v - v'.u}}{{{v^2}}}$

Công thức đặc biệt: $\left( {\frac{1}{x}} \right)' = \frac{{ - 1}}{{{x^2}}};\left( {\frac{1}{u}} \right)' = - \frac{{u'}}{{{u^2}}}$

B. Đạo hàm của hàm phân thức bậc 1/ bậc 1

$y = \frac{{ax + b}}{{cx + d}} \Rightarrow y' = \frac{{ad - bc}}{{{{\left( {cx + d} \right)}^2}}}$

C. Đạo hàm của hàm phân thức bậc 2/ bậc 1

$y = \frac{{a{x^2} + bx + c}}{{dx + e}} \Rightarrow y' = \frac{{ad{x^2} + 2aex + be - cd}}{{{{\left( {dx + e} \right)}^2}}}$

D. Đạo hàm của hàm phân thức bậc 2/ bậc 2

$\begin{matrix} y = \dfrac{{{a_1}{x^2} + {b_1}x + {c_1}}}{{{a_2}{x^2} + {b_2}x + {c_2}}} \Rightarrow y' = \dfrac{{\left| {\begin{array}{*{20}{c}} {{a_1}}&{{b_1}} \\ {{a_2}}&{{b_2}} \end{array}} \right|{x^2} + 2\left| {\begin{array}{*{20}{c}} {{a_1}}&{{c_1}} \\ {{a_2}}&{{c_2}} \end{array}} \right|x + \left| {\begin{array}{*{20}{c}} {{b_1}}&{{c_1}} \\ {{b_2}}&{{c_2}} \end{array}} \right|}}{{{{\left( {{a_2}{x^2} + {b_2}x + {c_2}} \right)}^2}}} \hfill \\ \Rightarrow y' = \dfrac{{\left( {{a_1}{b_2} - {a_2}{b_1}} \right){x^2} + 2\left( {{a_1}{c_2} - {a_2}{c_1}} \right)x + {b_1}{c_2} - {b_2}{c_1}}}{{{{\left( {{a_2}{x^2} + {b_2}x + {c_2}} \right)}^2}}} \hfill \\ \end{matrix}$

E. Công thức tính nhanh đạo hàm của một số hàm số thường gặp

Hàm số bậc nhất/bậc nhất: f(x)=ax+b/cx+d⇒f′(x)=ad−bc/(cx+d)².

Hàm số bậc hai/bậc nhất: f(x)=ax²+bx+c/mx+n⇒f(x)=amx²+2anx+bn−cm/(mx+n)²

Hàm số đa thức bậc ba: f(x)=ax³+bx²+cx+d⇒f(x)=3ax²+2bx+c

Hàm số trùng phương: f(x)=ax⁴+bx²+c⇒f′(x)=4ax³+2bx.

Hàm số chứa căn bậc hai: f(x)=√u(x)⇒f′(x)=u′(x)/2√u(x)

Hàm số chứa trị tuyệt đối: f(x)=|u(x)|⇒f′(x)=u′(x).u(x)/|u(x)|.

II. Ví dụ minh họa

Ví dụ: Tính đạo hàm của hàm số $y = \frac{{3{x^2} - 2x + 1}}{{{x^2} + x + 2}}$

Hướng dẫn giải

$y = \frac{{3{x^2} - 2x + 1}}{{{x^2} + x + 2}} \Rightarrow y' = \frac{{\left| {\begin{array}{*{20}{c}} 3&{ - 2} \\ 1&1 \end{array}} \right| + 2\left| {\begin{array}{*{20}{c}} 3&1 \\ 1&2 \end{array}} \right|x + \left| {\begin{array}{*{20}{c}} { - 2}&1 \\ 1&2 \end{array}} \right|}}{{{{\left( {{x^2} + x + 2} \right)}^2}}} = \frac{{5{x^2} + 10x - 5}}{{{{\left( {{x^2} + x + 2} \right)}^2}}}$

Ví dụ: Tính đạo hàm của hàm số $y = \frac{{3{x^2} - 2x + 1}}{{x + 2}}$

Hướng dẫn giải

$y = \frac{{3{x^2} - 2x + 1}}{{x + 2}} \Rightarrow y' = \frac{{3.1{x^2} + 2.3.2x + \left( { - 2} \right).2 - 1.1}}{{{{\left( {x + 2} \right)}^2}}} = \frac{{3{x^2} + 12x - 5}}{{{{\left( {x + 2} \right)}^2}}}$

Ví dụ: Tính đạo hàm của hàm số:

a. $y = \frac{{3x - 2}}{{x - 1}}$

b. $y = \frac{{x + 5}}{{2x + 3}}$

Hướng dẫn giải

a. $y' = \frac{{3.\left( { - 1} \right) - \left( { - 2} \right).1}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{ - 1}}{{{{\left( {x - 1} \right)}^2}}}$

b. $y' = \frac{{1.3 - 5.2}}{{{{\left( {2x + 3} \right)}^2}}} = \frac{{ - 7}}{{{{\left( {2x + 3} \right)}^2}}}$

III. Bài tập vận dụng

Câu 1: Đạo hàm của hàm số y= - 18√2 là:

A . - 18 B. 18 C. - 18√2 D. 0

Lời giải:

Hàm số y= - 18√2 là hàm hằng nên y'=0

Chọn D.

Câu 2: Cho hàm số y= f(x) = - 2x + 10. Trong các mệnh đề sau, mệnh đề nào đúng?

A.f' (x)=2 B. f'(x)= - 2 C. f' (x)=10 D. f' (x)=-10

Lời giải:

Ta có: f' (x)=(-2x+10)'=(-2x)'+( 10)'=-2-0= -2

Chọn B.

Câu 3: Cho hàm số y= -x² - 7x + 8. Tính đạo hàm của hàm số đã cho

A. –x- 7 B. 2x + 7

C. 2x - 7 D. -2x- 7

Lời giải:

Ta có: f' (x)=(-x²-7x+8)'=-(x )'-7.(x)'+(8)'=-2x-7.1+0

⇒ f’(x)= -2x - 7

Chọn D.

Câu 4: Đạo hàm của hàm số y= f(x)= 2x⁴ + 2x² + x + 28 là

A. 8x³ +2x + 1 B. 8x³ +4x+ 1

C. 8x⁴ + 4x + 1 D. 4x³ +2x+ 1

Lời giải:

Ta có: f' (x)=(2x⁴+2x²+x+28)'=2(x⁴ )'+2(x² )'+(x)'+(28)'

⇒f’(x)= 8x³ +4x + 1

Chọn B.

Câu 5: Đạo hàm của hàm số y= f(x)= (x- 6)(8- 4x) bằng biểu thức nào sau đây?

A. 32- 8x B. 6x- 24 C. - 4x + 32 D. 2x+ 16

Lời giải:

Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

f' (x)=( x-6)'.( 8-4x)+( x-6).(8-4x)'

⇒ f'(x)= 1.( 8 - 4x)+ (x- 6). (-4) = 8- 4x – 4x + 24 = -8x + 32

Chọn A.

Câu 6: Đạo hàm của hàm số y=f(x)= (x+ 2)( x- 3) bằng biểu thức nào?

A. x+ 1 B. 2x- 1 C. 3x+ 2 D. x²- 1

Lời giải:

+ Áp dụng công thức: (u.v)'=u'.v+u.v' ta có:

⇒ f' (x)=(x+2)'.(x-3)+(x+2).(x-3)'

= 1.(x-3) + (x+2). 1 = x- 3+ x+ 2

= 2x - 1

Chọn B.

Câu 7: Tính đạo hàm của hàm số y= (x-6)/(2x+3)?